1 Introduction
The functionality of critical infrastructures (CIs) is essential for both society and economy. Recent incidents have demonstrated that the impact of a disruption of a CI may be huge and involves cascading effects that have not been expected at first. For example, the blackout in Italy in 2003 was triggered by failure of two power lines in Switzerland according to a report of UCTE [35]. As interdependencies between critical infrastructures increase the analysis of an incident and its consequences gets more complex. Especially, the list of potential attacks and thus the list of available countermeasures will always be incomplete. Further, the effect of an attack involves a lot of uncertainty since it can never be perfectly predicted due to the many influencing factors that cannot be controlled, such as the current condition of CI, weather conditions or legal restrictions. In order to capture this uncertainty, we apply a probabilistic model to describe the (random) interaction between CIs and the consequences of a failure of one CI on the other CIs.
Several recent reports, for example by the Royal Academy of Engineering [25], the Lloyd’s Register Foundation [18] or Arup together with the University College London (UCL) [34], have highlighted the importance of resilient infrastructures for the functioning of modern society and economy. Furthermore, the resilience of an infrastructure or network of infrastructures is an important measure, for example for coordination of first responders in case of an incident or crisis situation. It is important for the coordinator of the response action to have a realistic estimate of what infrastructures are at risk of failure either as a direct effect of an incident or due to critical dependencies. While there are several examples of how to estimate risk in the context of risk management, like the widely accepted definition in ISO 31000 [11], a similar metric for resilience seems to be missing in the literature.
Our notion of resilience is based on the estimated impact deduced from the probabilistic model as well as on the countermeasures a CI takes to protect itself (which will be described through a variable termed preparedness). Both the impact and the preparedness are risk-specific, i.e., these values can only be determined in a given context. An overall measure of resilience is then obtained by considering a collection of risks and combining the results of the risk-specific analyses. We demonstrate how to include all the parameters that are commonly associated with resilience, yet operate at a level that combines those parameters in an intuitive way, and is thus designed for suitability as a resilience management metric similar to the ISO 31000 risk management considerations. Furthermore, we will show how the relevant parameters can be obtained in a way that reflects the complexity of critical infrastructure networks and is able to take dependencies into account. We illustrate our approach with the running example of a hospital depending on electricity, water and a transportation system.
1.1 Paper Outline
The remainder is organized as follows: after a recap of the current research situation in Sect. 2, Sect. 3 introduces our model for resilience of a critical infrastructure inside a network of interdependent CIs. Section 4 shows a computational example. Finally, we provide concluding remarks in Sect. 5.
2 Related Work
Since the early work on critical infrastructure dependencies presented by Rinaldi, Peerenboom and Kelly [24], a lot of research has been carried out to better understand and model dependencies between critical infrastructures and simulate the interactions that influence the security and safety of those infrastructures. For example, Setola et al. [27] propose a model to assess cascading effects through critical infrastructure dependencies using the input-output inoperability model (IMM), D’agostino et al. present an approach based on extended Leontief models [6]. Svendsen and Wolthusen [29] propose a graph based model to understand critical infrastructure interdependencies and Theocharidou et al. [31] present a risk assessment methodology for critical infrastructures with a focus on dependencies. Schaberreiter et al. [26] present an interdependency modeling and simulation approach for on-line risk monitoring in interdependent critical infrastructures based on a Bayesian network. With a few exceptions, critical infrastructure interdependency research has been conducted to better understand risks and threats. Critical infrastructure resilience has not been the main focus of this research so far, especially in the context of organizational resilience management.
Various definitions of the term resilience exist in the literature in different areas [33], e.g., an overview on different definitions in the field of supply chains is given in [12]. In [16], Hollnagel et al. provide an excellent overview to resilience and resilience engineering in the safety context. The report presented in [20] builds on those definitions to argue about how resilience can be applied on an operational level to interdependent infrastructure systems. While significant initial work is identified, it is concluded that scientific research in the field of resilience is still in its infancy, and that the integration of institutional elements that define the complexity of real-world interdependent infrastructures, as well as the current lack of universally applicable resilience metrics, are two main factors that need to be further substantiated.
Shen and Tang [28] propose a resilience assessment framework for critical infrastructure systems. They identified three resilience capacities for CI systems: The absorptive capacity (the ability of systems to absorb incidents) the adaptive capacity (the ability of systems to adapt to an incident) and the restorative capacity (the ability of systems to be repaired easily). The resilience framework however does not rely on those parameters, it is rather based on the interplay between two random variables: The severity of an event and the recovery time of an infrastructure system. While such a framework can provide a high level estimate of resilience, it seems to lack the modeling depth required to understand the complex interactions in CI environments. Creese et al. [4] take a top-down modeling approach on resilience that allows a high degree of flexibility and modularity since elements can be incrementally refined to the required level of detail. External events can be taken into account, and the framework should encourage joint risk mitigation for a more resilient CI network. The framework is based on an identification of assets and internal/external dependencies on the enterprise, information, technology and physical layers. The actual dependency assessment is based on the creation of a dependency graph, capturing the different relations nodes in the graph can have. Resilience determination is achieved via what-if analysis based on this graph. Hromada and Ludek [19] argue the importance of the resilience of critical infrastructure systems when evaluating resilience of those systems. They state that the two main positive influences on the resilience of a systems are the preparedness of the system against a threat and the resilience of the system against this threat, and that resilience is mainly influenced by the structural resilience and the security resilience. The authors illustrate how to derive those two resilience coefficients using a case from the energy sector.
Liu and Hutchison [17] propose to achieve resilience through situational awareness. Building on a situational awareness system, the authors argue that by observing specified classes of network characteristics, a decision maker can derive counter measures for discovered problems based on a holistic understanding of the system gained with situational awareness, and improve the resilience of the network in the process. Gouglidis et al. [9] propose a similar approach to improve critical infrastructure resilience, basing the situational awareness considerations on threat awareness. In this context, a set of metrics is derived for a European utility network in [10].
Many proposed resilience models are specific to a CI sector, to a concrete use case or to a specific threat. For example, Tokgoz and Gheorghe [32] present a resilience model for residential buildings in case of hurricane winds. Panteli et al. [23] propose resilience metrics for the energy sector with a focus on quantifying high impact low probability events. Cuisong and Hao [5] propose resilience measures for water supply infrastructure with a focus on the effects of rapidly changing urban environments on the supply system. While those examples of resilience measures based on specific sectors or concrete use cases can give valuable insight into the resilience requirements of the different sectors, our approach aims to capture infrastructure resilience on a higher conceptual level, taking into account the influences dependent infrastructures have on the resilience. We argue that a trade-off between modeling depth and abstraction is required to achieve this goal.
While the resilience research so far includes both framework based approaches and use cases, none of these works has proposed a resilience metric aimed at resilience management, similar to the risk management metric proposed in ISO 31000, taking into account the risks critical dependencies pose on resilience. The advantage of such a metric is its applicability to the diverse and vastly different set-ups in critical infrastructures or complex organizational set-ups, useful to both the management of such infrastructures to be able to better direct investment in resilience enhancing measures, and to first responders to better direct and coordinate response actions in case of an incident. Such a measure should be in line with state-of-the art cybersecurity efforts like the NIST cybersecurity framework [21], or on a European level, the legislative requirements for critical infrastructures implemented in the network and information security (NIS) directive [30]. The additional effort to derive a resilience metric based on regular organizational risk management according to ISO 31000 (or other methodologies like OCTAVE [1], CRAMM [36], ISRAM [13]) should be kept minimal.
3 A Model for Resilience of a Critical Infrastructure
Definitions of resilience are manifold and mostly qualitative. Among the proposals are [20]: “the capacity of the system to return to its original state after shocks”, or an amended version thereof calling it the“possibility of reaching a new stable state, possibly different from the original state”, up to more recent ones [16]: “system that can sustain its function by constantly adjusting itself prior, during and after shocks” and “how the system can function under different scenarios”, as well as [25]: “the capacity of a system to handle disruptions to operation” and [18]: “the ability to withstand, respond and/or adapt to a vast range of disruptive events by preserving and even enhancing critical functionality”. All these understandings are sufficiently similar to admit a common denominator upon which we propose a way to measure the resilience of a critical infrastructure for a specific situation. Hereafter, we shall understand resilience as the ability of an infrastructure to maintain operation despite the realization of a risk scenario. That is, the extent to which an impact of incident affects the infrastructure on providing its input to other dependent CIs and to the society.
In an increasingly interconnected world, resilience of a critical infrastructure does not only depend on external incidents interrupting the normal operation and on available countermeasures inside the CI but also on the condition of other CIs on which the CI under consideration depends. We argue that the resilience of a CI asset can be determined by setting, for each relevant risk against the asset, the impact of the risk in relation to the preparedness against this risk. A metric that describes the resilience of an asset against all relevant risks can be obtained by summing up the risk-specific resilience metric according to the estimated likelihood of the risk. While preparedness and likelihood are assumed to be mostly qualitative measures that can be obtained in known ways in the context of traditional organizational risk analysis (e.g., expert interviews), the impact of a risk – having in mind interconnectedness of critical infrastructures – is a crucial value that heavily influences the accuracy of resilience estimation. We therefore propose a quantitative impact measure which is a simulation based and risk-specific impact estimation that takes into account the impact of critical dependencies in relevant risk scenarios. Eliciting these values is a matter of classical risk assessment and as such aided by the palette of existing standards in the area (like ISO and others, as mentioned in Sect. 2). Nonetheless, the information can partly be obtained from simulations, such as the likelihood of an incident to have an impact (not telling how big it would be) at all on a CI. Especially for the case of the likelihood parameter, such values are expectedly difficult for a person to quantify, so simulations can (and should) be invoked as auxiliary sources of information (e.g., [14, 22] to mention only two examples). We stress that the simulation is a nonlinear model and distinct from the resilience model. The simulation is based on knowledge about the system dynamics. It provides input for the actual linear resilience model intended for resilience management. The two models are thus separate, and the simulation model can be replaced by other means of obtaining the respective parameters (if more relevant to a specific use case).
Preparedness is the entirety of the preparatory measures taken at asset A against a risk scenario s, e.g., an insurance. Formally, we quantify the preparedness by a number 
that reduces the impact accordingly (for example, by reducing the damage to a lower impact level through insurance recovery payments), and hence is measured on the same scale as the impact. In the following sections, we formalize our resilience metric, describe which qualitative parameters are required for this metric, and how the impact of an incident will later be simulated in order to facilitate the computation.
3.1 A Measure of Resilience
” we define the resilience of a CI A as![$$\begin{aligned} R(A)=\sum _{s=1}^N \omega _s \cdot (P_{s,A}-\mathsf {E}[I_{s,A}]), \end{aligned}$$](../images/477940_1_En_5_Chapter/477940_1_En_5_Chapter_TeX_Equ1.png)
is the probability of scenario s to occur, ![$$\mathsf {E}[I_{s,A}]$$](../images/477940_1_En_5_Chapter/477940_1_En_5_Chapter_TeX_IEq4.png)
denotes the expected impact for the CI A under scenario s and 
denotes the preparedness of the CI A in case s occurs. Note that 
, unlike the other parameters, is independent of the asset A, since the likelihood for a scenario to occur is the same for all assets, but each of them can suffer different impacts depending on their importance, structure and preparedness levels. To ease notation in the following, let us take the asset A as generically arbitrary but fixed, and omit the dependence of the impact and preparedness to ease the notation (the asset to which the values refer will be clear from the context) towards writing R, 
and ![$$\mathsf {E}[I_s]$$](../images/477940_1_En_5_Chapter/477940_1_En_5_Chapter_TeX_IEq8.png)
for the resilience, preparedness and expected impact (under scenario s).We stress that for N different scenarios, the impact relates to failure, loss or other damage to an asset conditional on the scenario to become reality. That is, the expected impact would be obtained from simulations, where a specific scenario is assumed to happen (say, fire, earthquake, cyber attack, etc.) which causes some assets to fail which in turn affects asset A.
The result from Eq. (1) is a number that can be interpreted as follows. Large positive values of R indicate a high robustness, a value of zero indicates that on average the preparedness equals the expected damage and large negative values indicate that there is still some potential to improve protection of the infrastructure (at least for some scenarios s). More explicitly, for each risk scenario s the value ![$$P_s-E[I_s]$$](../images/477940_1_En_5_Chapter/477940_1_En_5_Chapter_TeX_IEq9.png)
is positive if the CI A is “well prepared” against the risk scenario s, that is, the expected impact is smaller than the preparedness. Thus, if the weighted average over all scenarios is still positive (i.e., 
), we can think of the corresponding CI as being resilient. Similarly, if the average is negative the CI does not seem to be sufficiently prepared against the various risk scenarios. The definition in (1) also agrees with the intuition that a well prepared CI is more resilient, i.e., a high value of 
increases the value of ![$$P_s-E[I_s]$$](../images/477940_1_En_5_Chapter/477940_1_En_5_Chapter_TeX_IEq12.png)
and thus of R. Finally, the structure of the formula accounts for the fact that preparedness has only an influence on the impact, but none on the likelihood: for example, a fire insurance reduces the impact of a fire, but leaves the (natural) chances of this to happen unchanged. This is not necessarily reflected in other related formulas in the area, such as the ISO heuristic [11] being 
. Herein, status refers to the level of preparedness or degree of implementation of countermeasures against the respective risk. It is, however, obvious that the associativity of the multiplication would let the status hereby be treated as affecting either the impact (plausible) or the likelihood (implausible), or even both (also implausible). Contrary to this, the above convention (1) is designed to avoid this implausibility. The expected value ![$$\mathsf {E}[I_s]$$](../images/477940_1_En_5_Chapter/477940_1_En_5_Chapter_TeX_IEq14.png)
of the impact of a realization of risk scenario s can be estimated by the use of simulations, as described in more detail below.
Since CIs can choose their own interpretation of the scale describing its states, a competition between infrastructures in terms of maximizing resilience can be avoided because the values are not directly comparable.
3.2 Parameter Estimation
In order to obtain estimates for the parameters required for the proposed resilience metric, an analysis of the CI is necessary. While much of the required information and assessments may be derived from traditional risk assessment results, the aim of this section is to outline the steps to obtain the results specific to our approach. Our assessments are based on an identification of critical assets within CIs, and the internal and external dependencies between those assets that influence the availability to the asset. Thus, the first step in our analysis consists of representing the various CIs as a graph where each CI is represented as a node and each dependency is represented as a directed edge from the CI providing input to the dependent CI (sometimes called input provider). From this high-level representation of a CI network, each CI operator can substantiate the asset and dependency list for their own infrastructure based on their organizational set-up and on their individual understanding of the most important internal and external dependencies.
We assume that the various dependencies can be classified, i.e., we have a predefined set of “types” of dependencies (say, n different types) and to each edge exactly one type is assigned. Such classification has been used in earlier work on dependencies between critical infrastructures [24]. Example types include (but are not limited to) geographical dependencies (e.g., spatial proximity), logical dependency (e.g., a client-server relation), physical dependency (e.g., between the hardware and the software application that runs or otherwise depends on it) and social dependency (e.g., local inhabitants depending on an infrastructure and thus being affected by its outage). In our model we consider the classes“minor”, “normal” and“critical” to characterize the dependencies between assets. Each class is then represented by a classical probability, i.e., a value between 0 and 1.
In the next step, the most relevant risk scenarios that influence the availability of an asset are identified, for example by assessing the relevance of specific risks from a risk catalog. This results in a list of, say, the N most important risks. This list is extended with the likelihood of occurrence, denoted by 
for risk scenario s with 
. These values need to be estimated from historical data (where available) or from experts familiar with the CI. Similar to the likelihood, the preparedness 
of a CI against risk scenario s can be estimated. The scale for this qualitative estimation needs to be a trade-off between giving an expert doing the assessment the option of fine-grained choice, and the practicality of an assessment. For our model, we have chosen a predefined qualitative scale from 1 (corresponding to smooth operation) to 5 (corresponding to total failure). The simulation based impact estimation, which will be described in the next section, also requires qualitative estimates. Unlike likelihood and preparedness, which both depend on the specific risk scenario, the parameters required for the impact only depend on the asset as it describes the consequences of a (partial) failure of another CI. Similarly as for the preparedness, we assume that the impact of each asset is described through a state between 1 and 5 with intermediate states indicating a certain degree of interruption of operation. For each dependency type, an assessment of the most likely state of an asset needs to be estimated, given the current state of its provider. This results in a state transition matrix for each dependency type, enabling the simulation-based impact estimation.
3.3 Impact Estimation
The dynamics of the consequences of an incident are described through a stochastic model as introduced in [14]. This model assumes that due to problems in a CI (i.e., the CI is in a state where it does not operate smoothly, which is represented by a state value larger than 1) the CI depending on it changes its state with a certain probability. In the case of a hospital, if the electricity provider faces some problems this should not affect the hospital too much due to the availability of an emergency power system. However, if this system fails (which happens with a very low probability), then the effect would be enormous, so there is a small chance that the state of the hospital is very bad (which is represented by a high value). These likelihoods of a state change in a CI due to a reduced availability of one of its input providers need to be assigned for every type of connection and every risk by experts familiar with the CI. This procedure can be simplified (and the quality of data improved) by allowing experts to only assess the values of that part of the CI they are familiar with. Furthermore, the framework can handle disagreeing (inconsistent) estimates [15] so experts are not forced to consent to a single value as representative for a heterogeneous opinion pool (thus avoiding the consensus problem). Based on this model, the propagation of an incident in a network of interdependent CIs can be simulated which allows estimating the impact of an incident (realized risk) on a specific critical infrastructure. More explicitly, it yields an empirical probability distribution over all possible impacts, as discussed next.
4 An Illustrative Example
-
Earthquake
-
Blackout
-
Water contamination
mostly influences the transportation system, i.e., its state changes from 1 to 3 which corresponds to serious problems (e.g., roads are blocked). Scenario 
on the other hand influences the electricity provider and causes it to change its state from 1 to 4 (that is, heavy damage but not complete failure). The water contamination scenario 
finally causes a problem for the water provider to some extent, so we assume it changes its state form 1 to 2 if this scenario becomes real (i.e., there are some problems with providing drinking water but other services such as cooling water should still be possible).4.1 Parameter Estimation
As described in Sect. 3, the next step is to estimate the parameters needed to compute the resilience value (1).
Likelihood of risk scenario and preparedness level
Risk | Risk likelihood | Preparedness level |
|---|---|---|
| 0.2 | 3 |
| 0.3 | 4 |
| 0.2 | 3 |
For illustrative purposes only (and not claiming any accuracy of these values for reality), the parameters 
are here chosen based on available scientific considerations and reports on the respective scenarios that allows us an “educated guess”. We let 
(earthquake) be 0.2 (see [7] for more accurate data), 
(blackout) be 0.3 (see [8] for a formal treatment of such likelihoods based on a given power supply system), and 
(water contamination) be 0.2 (see [2, 3] for systematic methods to get realistic figures for real scenarios). In any practical case, these likelihoods would be w.r.t. a fixed period of foresight (say, the probability of an earthquake to occur within the next 30 years). The values for the preparedness parameter can be seen as the amount of damage that can still be handled in the sense that due to the implemented counter measures operation is still possible up to a desired level. We chose values 3 and 4 to describe the situation where a CI is equipped against a medium (3) or high (4) damage. While it is often desirable to have a maximal protection, this also involves resources and monetary cost so that the actual level of protection also depends on the expected impact and on the likelihood of occurrence (i.e., no one is willing to invest a lot of effort to protect against a very unlikely risk that causes only limited damage).
State Transitions: As detailed in Sect. 3.2, we assume that the transmission matrices are characteristic to the CI (asset) we consider, but do not change with the concrete risk scenario we look at. This assumption is based on the observation that the main factor describing the impact of a (partial) failure of a provider is the condition of the CI. In particular, it depends on factors such as the geographical location of the CI or on the availability of substitutes and only to a very limited degree on the scenario that causes trouble for a provider.
To ease matters of modeling, we propose grouping dependencies into a few distinct classes, each of which can be represented by its own transition matrix. For example, a dependency of a CI X on another CI Y may be minor, if the outage of Y can be bridged (if temporarily) or substitutes are available to X (on a permanent loss of Y); thus we expect only negligible impact. Likewise, the dependency can be normal, if the outage of Y will have an impact on X that does not cause X itself to fail, but continue with limited services. Finally, a dependency can be critical, if X vitally depends on Y and an outage of Y with high likelihood implies the subsequent outage of X. The difference between these dependencies is then to some extent reflected in the setting of the transitions and transition matrices shown next as 
and 
. For a minor dependency, say if there is an outage and thus Y is in state 5, there is only a small likelihood of 0.1 for X to fail upon this (as indicated by the last entry in the last row of the corresponding matrix). On the other hand, for a critical dependency, the same scenario bears a likelihood of 0.8 for X to fail if Y breaks down.
4.2 Impact Estimation
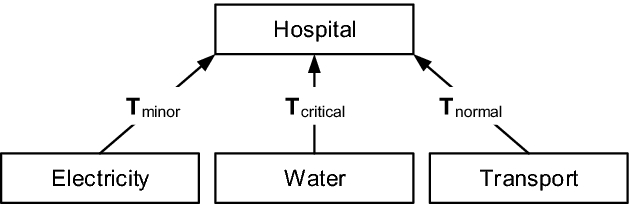
Upstream CI dependencies in our hospital example
For each CI we consider five possible states where 1 represents smooth operation and 5 represents total failure (and intermediate states correspond to limited operation). For a specific risk scenario the dependency matrices 
describe the dynamics of the system of interconnected CIs where the ij-th entry corresponds to the conditional likelihood 
CI gets into state j | provider is in state i), i.e., this stochastic matrices describe the (random) consequences of the various states of a provider on the dependent CI. For a specific risk scenario s the impact of an incident on a CI can be empirically estimated as described in [14].
, 
and 
, respectively, based on 
repetitions of the simulation of the stochastic dependency.Simulated likelihoods (relative frequencies) for CI status under different risk scenarios
Risk scenario | CI status | ||||
|---|---|---|---|---|---|
1 | 2 | 3 | 4 | 5 | |
| 0.052 | 0.152 | 0.277 | 0.311 | 0.208 |
| 0.035 | 0.115 | 0.228 | 0.443 | 0.179 |
| 0.048 | 0.150 | 0.281 | 0.314 | 0.207 |
![$$\mathsf {E}[I_{s,A}]$$](../images/477940_1_En_5_Chapter/477940_1_En_5_Chapter_TeX_IEq42.png)
in (1) by weighting the impacts with the respective likelihoods. The results are shown in Table 3. For simplicity and transparency of the example calculations here, we let the impact be equal to the CI status. Expected impact for each considered risk scenario
Scenario |
|
|
|
|---|---|---|---|
Expected Impact | 3.471 | 3.616 | 3.482 |
![$$E[I_{s,A}]$$](../images/477940_1_En_5_Chapter/477940_1_En_5_Chapter_TeX_IEq46.png)
4.3 Resilience
![$$\begin{aligned} R(A)=\sum _{s=1}^N \omega _s \cdot (P_{s,A}-\mathsf {E}[I_{s,A}])= -0.0754, \end{aligned}$$](../images/477940_1_En_5_Chapter/477940_1_En_5_Chapter_TeX_Equ4.png)
from level 3 to level 4, we get![$$\begin{aligned} R(A)=\sum _{s=1}^N \omega _s \cdot (P_{s,A}-\mathsf {E}[I_{s,A}])= 0.1246, \end{aligned}$$](../images/477940_1_En_5_Chapter/477940_1_En_5_Chapter_TeX_Equ5.png)
5 Conclusion and Future Work
Managing critical infrastructures is a matter that can benefit from mathematical models, but is ultimately too complex to be left to any simplified mathematical formula. Similarly as how risk measures serve as guiding benchmarks, resilience measures can play the role of pointers towards weak and strong parts of an infrastructure.
Likewise, risk can be taken as a “global” indication to take action against certain scenarios, whereas resilience can serve as a “local” indicator on where to take the action. A decision maker can thus first prioritize risks based on their magnitude, and then continue for each risk to rank CIs based on their resilience against a risk scenario so as to recognize where the demand for additional security is the most.
Simulation studies as carried out in the worked example may provide a valuable source of data for computing risk and resilience, since likelihood is often an abstract term whose mere magnitude already can create misinterpretations (the fact that people over-, resp. underestimate low and large likelihoods, as well as they differently weigh impacts is at the core of social choice theories like prospect theory and others). The measure proposed here is designed for “compatibility” with existing (standard) notions of risk, and can be generalized in various ways. The aforementioned psychological factors of over- and under-weighting of impacts and likelihoods can be integrated as nonlinear functions wrapped around the parameters in formula (1). The degree to which this is beneficial over the direct version of (1) is a matter of empirical studies and as such outside the scope of this work. Still, we emphasize it as a generally interesting aisle of future research.
Acknowledgment
This work was done in the context of the project “Cross Sectoral Risk Management for Object Protection of Critical Infrastructures (CERBERUS)”, supported by the Austrian Research Promotion Agency under grant no. 854766.