Chapter 12
Making Waves: An Overview of Sound
In This Chapter
Working with sound waves
Getting grounded in the physics needed to understand speech
Relating sound production to your speech articulators
One of the great things about phonetics is that it’s a bridge to fields like acoustics, music, and physics. To understand speech sounds, you must explore the world of sound itself, including waves, vibration, and resonance. Many phoneticians seem to be musicians (either at the professional level or as spirited amateurs), and it’s normal to find phoneticians hanging around meetings of the Acoustical Society of America. Just trying to talk about this accent or that isn’t good enough; if you want to practice good phonetics, you need to know something about acoustics.
This chapter introduces you to the world of sound and describes some basic math and physics needed to better understand speech. It also explains some essential concepts useful for analyzing speech with a computer.
Defining Sound
Sound refers to energy that travels through the air or another medium and can be heard when it reaches the ear. Physically, sound is a longitudinal wave (also known as a compression wave). Such a wave is caused when something displaces matter (like somebody’s voice yelling, “Look out for that ice cream truck!”) and that vibration moves back and forth through the air, causing compression and rarefaction (a loss of density, the opposite of compression). When this pressure pattern reaches the ear of the listener, the person will hear it.
When a person shouts, the longitudinal wave hitting another person’s ear demonstrates compression and rarefaction. The air particles themselves don’t actually move relative to their starting point. They’re simply the medium that the sound moves through. None of the air expelled from the person shouting about the truck actually reaches the ear, just the energy itself. It’s similar to throwing a rock in the middle of a pond. Waves from the impact will eventually hit the shore, but this isn’t the water from the center of the pond, just the energy from the rock’s impact.
The speed of sound isn’t constant; it varies depending on the stuff it travels through. In air, depending on the purity, temperature, and so forth, sound travels at approximately 740 to 741.5 miles per hour. Sound travels faster through water than through air because water is denser than air (the denser the medium, the faster sound can travel through it). The problem is, humans aren’t built to interpret this faster signal in their two ears, and they can’t properly pinpoint the signal. For this reason, scuba diving instructors train student divers not to trust their sense of sound localization underwater (for sources such as the dive boat motor). It is just too risky. You can shout at someone underwater and be heard, although the person may not be able to tell where you are.
Cruising with Waves
The universe couldn’t exist without waves. Most people have a basic idea of waves, perhaps from watching the ocean or other bodies of water. However, to better understand speech sounds, allow me to further define waves and their properties.
Here are some basic facts about sound and waves:
Sound is energy transmitted in longitudinal waves.
Because it needs a medium, sound can’t travel in a vacuum.
Sounds waves travel through media (such as air and water) at different speeds.
Sine (also known as sinusoid) waves are simple waves having a single peak and trough structure and a single (fundamental) frequency. The fundamental frequency is the basic vibrating frequency of an entire object, not of its fluttering at higher harmonics.
People speak in complex waves, not sine waves.
Complex waves can be considered a series of many sine waves added together.
Fourier analysis breaks down complex waves into sine waves (refer to the sidebar later in this chapter for more information).
Complex waves can be periodic (as in voiced sounds) or aperiodic (as in noisy sounds). Check out the “Sine waves” and “Complex waves” sections for more on periodic and aperiodic waves.
These sections give examples of simple and complex waves, including the relation between the two types of waveforms. I also describe some real-world applications.
Sine waves
The first wave to remember is the sine wave (or sinusoid), also called a simple wave. Sine is a trigonomic function relating the opposite side of a right-angled triangle to the hypotenuse.
There are some good ways to remember sine waves. Here is a handy list:
Sine waves are the basic building blocks of the wave world.
All waveforms can be broken down into a series of sine waves.
Many things in nature create sine waves — basically anything that sets up a simple oscillation. Figure 12-1 shows a sine wave being created as a piece of paper is pulled under a pendulum that’s swinging back and forth.
In western Texas, if you’re lucky, you may see a beautiful sine wave in the sand left by a sidewinder rattlesnake.
When sound waves are sine waves, they’re called pure tones and sound cool or cold, like a tuning fork or a flute (not a human voice or a trumpet). This is because the physics of sine wave production involve emphasizing one frequency, either by forcing sound through a hole (as in a flute or whistle) or by generating sound with very precisely machined arms (which reinforce each other as they vibrate), in the case of the tuning fork).
Sine waves are used in clinical audiology for an important test known as pure-tone audiometry. Yes, those spooky tones you sometimes can barely hear during an audiology exam are sine waves designed to probe your threshold of hearing. This allows the clinician to rule out different types of hearing loss.
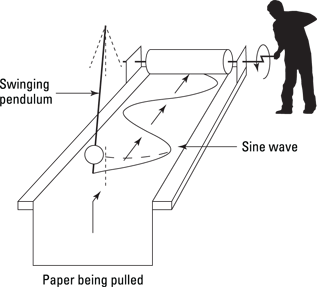
Illustration by Wiley, Composition Services Graphics
Figure 12-1: A pendulum creating sine waves on a piece of paper being pulled by an enthusiastic phonetician.
Complex waves
Everyone knows the world can be pretty complex. Waves are no exception. Unless you’re whistling, you don’t produce simple waves — all your speech, yelling, humming, whispering, or singing otherwise consists of complex wave production.
A complex wave is like a combination of sine waves all piled together. To put it another way, complex waves have more than one simple component — they reflect several frequencies made not by a simple, single vibrating movement (one pendulum motion) but by a number of interrelated motions. It’s similar to the way that white light is complex because it’s actually a mixture of frequencies of pure light representing the individual colors of the rainbow.
Getting into the formula of sine
If you like formulas, sine waves are created by the sine function:
y(t) = Asin(2πft + ϕ)
In this formula:
A: The amplitude is the peak deviation of the function from zero.
f: The frequency is the number of oscillations (cycles) that occur each second of time.
ϕ: The phase specifies (in radians) where in its cycle the oscillation is at t = 0.
If you aren’t a math fan, no worries!
Measuring Waves
Every wave can be described in terms of its frequency, amplitude, and duration. But when two or more waves combine, phase comes into play. In this section, you discover each of these terms and what they mean to sound.
Frequency
Frequency is the number of times something happens, divided by time. For instance, if you go to the dentist twice a year, your frequency of dental visits is two times per year. But sound waves repeat faster and therefore have a higher frequency.
Frequency is a very important measure in acoustic phonetics. The number of cycles per second is called hertz (Hz) after the famous German physicist Heinrich Hertz. Another commonly used metric is kilohertz (abbreviated kHz), meaning 1,000 Hertz. Thus, 2 kHz = 2,000 Hz = 2,000 cycles per second.
The range of human hearing is roughly 20 to 20,000 cycles per second, which means that the rate of repetition for something to cause such sound is 20 to 20,000 occurrences per second. A bullfrog croaks in the low range (fundamental frequency of approximately 100 Hz), and songbirds sing in the high range (the house sparrow ranges from 675 to 18,000 Hz).
Figure 12-2 shows a sample of frequency demonstrated with a simple example so that you can count the number of oscillations and compute the frequency for yourself. In Figure 12-2a (periodic wave), you can see that the waveform (the curve showing the shape of the wave over time) repeats once in one second (shown on the x-axis). Therefore, the frequency is one cycle per second, or 1 Hz. If this were sound, you couldn’t hear it because it’s under the 20 to 20,000 Hz range that people normally hear.
Seeing is believing! An oscillation can be counted from peak to peak, valley to valley, or zero-crossing to zero-crossing.
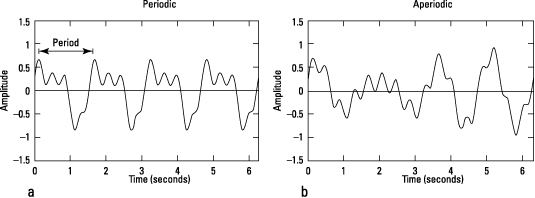
Illustration by Wiley, Composition Services Graphics
Figure 12-2: A sample periodic wave (a) and an aperiodic wave (b).
Period is a useful term related to frequency — it’s a measure of the time between two oscillations and the inverse of frequency. If your frequency of dental visits is two times per year, your period of dental visits is every six months.
Waves produced by irregular vibration are said to be periodic. These waves sound musical. Sine waves are periodic, and most musical instruments create periodic complex waves. However, waves with cycles of different lengths are aperiodic — these sound more like noise. An example would be clapping your hands or hearing a hissing radiator. Figure 12-2b shows an aperiodic wave.
You can also talk about the length of the wave itself. You can sometimes read about the wavelength of light, for example. But did you ever hear about the wavelength of sound? Probably not. This is because wavelengths for sound audible to humans are relatively long, from 17 millimeters to 17 meters, and are therefore rather cumbersome to work with. On the other hand, sound wavelength measurements can be handy for scientists handling higher frequencies, such as ultrasound, which uses much higher frequencies (and therefore much shorter wavelengths).
One frequency that will come in very handy is the fundamental frequency, which is the basic frequency of a vibrating body. It’s abbreviated F0 and is often called F-zero or F-nought. A sound’s fundamental frequency is the main information telling your ear how low or high a sound is. That is, F0 gives you information about pitch (see the section ”Relating the physical to the psychological” in this chapter).
Amplitude
Amplitude refers to how forceful a wave is. If there is a weak, wimpy oscillation, there will be a tiny change in the wave’s amplitude, reflected on the vertical axis. Such a wave will generally sound quiet. Figure 12-3 shows two waves with the same frequency, where one (shown in the solid line) has twice the amplitude as the other (shown in the dotted line).
Sound amplitude is typically expressed in terms of the air pressure of the wave. The greater the energy behind your yell, the more air pressure and the higher the amplitude of the speech sound. Sound amplitude is also frequently described in decibels (dB). Decibel scales are important and used in many fields including electronics and optics, so it’s worth taking a moment to introduce them.
In the following list, I give you the most important things about dB you need to know:
One dB = one-tenth of a bel.
The bel was named after Alexander Graham Bell, father of the telephone, which was originally intended as a talking device for the deaf.
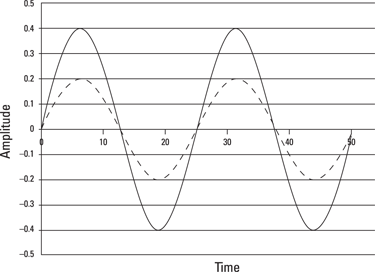
Illustration by Wiley, Composition Services Graphics
Figure 12-3: Two waveforms with the same frequency and different amplitude.
dB is a logarithmic scale, so an increase of 10 dB represents a ten-fold increase in sound level and causes a doubling of perceived loudness.
In other words, if the sound of one lawnmower measures 80 dB, then 90 dB would be the equivalent sound of ten lawnmowers. You would hear them twice as loud as one lawnmower.
Sound levels are often adjusted (weighted) to match the hearing abilities of a given critter. Sound levels adjusted for human hearing are expressed as dB(A) (read as “dee bee A”).
The dBA scale is based on a predefined threshold of hearing reference value for a sine wave at 1000 Hz — the point at which people can barely hear.
Conversational speech is typically held at about 60 dBA.
Too much amplitude can hurt the ears. Noise-induced hearing damage can result from sustained exposure to loud sounds (85 dB and up).
A property associated with amplitude is damping, the gradual loss of energy in a waveform. Most vibrating systems don’t last forever; they peter out. This shows up in the waveform with gradually reduced amplitude, as shown in Figure 12-4.
Duration
Duration is a measure of how long or short a sound lasts. For speech, duration is usually measured in seconds (for longer units such as words, phrases, and sentences) and milliseconds (ms) for individual vowels and consonants.
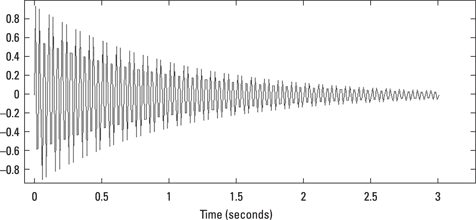
Illustration by Wiley, Composition Services Graphics
Figure 12-4: Damping happens when there is a loss of vibration due to friction.
Phase
Phase is a measure of the time (or angle) between two similar events that run at roughly the same time. Phase can’t be measured with a single sound — you need two (waves) to tango. Take a look at Figure 12-5 to get the idea of how it works:
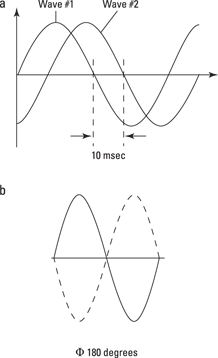
Illustration by Wiley, Composition Services Graphics
Figure 12-5: Two examples of phase differences — by time (a) and by angle (b).
In the top example of Figure 12-5, when wave #1 starts out, wave #2 lags by approximately 10 msec. That is, wave #2 follows the same pattern but is 10 msec behind. This is phase described by time.
The bottom example in Figure 12-5 shows phase described by angle. Two waves are 180 degrees out of phase. This example is described by phase angle, thinking of a circle, where the whole is 360 degrees and the half is 180 degrees. To be 180 degrees out of phase means that when one wave is at its peak, the other is at its valley. It’s kind of like a horse race. If one horse is a quarter of a track behind the other horse, you could describe him as being so many yards, or 90 degrees, or a quarter-track behind.
Relating the physical to the psychological
In a perfect world, what you see is what you get. The interesting thing about being an (imperfect) human is that the physical world doesn’t relate in a one-to-one fashion with the way people perceive it. That is, just because something vibrates with such and such more energy doesn’t mean you necessarily hear it as that much louder. Settings in your perceptual system make certain sounds seem louder than others and can even set up auditory illusions (similar to optical illusions in vision).
This makes sense if you consider how animals are tuned to their environment. Dogs hear high-pitched sounds, elephants are tuned to low frequencies (infrasound) for long-distance communication, and different creatures have different perceptual settings in which trade-offs between frequency, amplitude, and duration play a role in perception. Scientists are so intrigued by this kind of thing that they have made it into its own field of study — psychophysics, which is the relationship between physical stimuli and the sensations and perceptions they cause.
Pitch
The psychological impression of fundamental frequency is called pitch. High-frequency vibrations sound like high notes, and low-frequency vibrations sound like low notes. The ordinary person can hear between 20 to 20,000 Hz. About 30 to 35 percent of people between 65 and 75 years of age may lose some hearing of higher-pitched sounds, a condition called presbycusis (literally “aged hearing”).
Loudness
People hear amplitude as loudness, a subjective measure that ranges from quiet to loud. Although many measures of sound strength may attempt to adjust to human loudness values, to really measure loudness values is a complex process — it requires human listeners.
Different sounds with the very same amplitude won’t have the same loudness, depending on the frequency. If two sounds have the same amplitude and their frequencies lie between about 600 and 2,000 Hz, they’ll be perceived to be about the same loudness. Otherwise, things get weird! For sounds near 3,000 to 4,000 Hz, the ear is extra-sensitive; these sounds are perceived as being louder than a 1,000 Hz sound of the same amplitude. At frequencies lower than 300 Hz, the ear becomes less sensitive; sounds here are perceived as being less loud than they (logically) “should” be.
This means I can freak you out with the following test. I can play you a 300 Hz tone, a 1,000 Hz tone, and a 4,000 Hz tone, all at exactly the same amplitude. I can even show you on a sound-level meter that they are exactly the same. However, although you know they are all the same, you’ll hear the three as loud, louder, and loudest. Welcome to psychophysics.
Length
The psychological take on duration is length. The greater the duration of a speech sound, the longer that signal generally sounds. Again, however, it’s not quite as simple as it may seem. Some languages have sounds that listeners hear as double or twin consonants. (Note: Although English spelling has double “n,” “t,” and so forth, it doesn’t always pronounce these sounds for twice as long.) Doubled consonant sounds are called geminates (twins). It turns out that geminates are usually about twice the duration as nongeminates. However, it depends on the language. In Japanese, for example, geminates are produced about two to three times as long as nongeminates. An example is /hato/ “dove” versus /hatto/ “hat.”
Sound localization
Humans and other creatures use phase for sound localization, which allows them to tell where a sound is coming from. A great way to test whether you can do this is to sit in a chair, shut your eyes, and have a friend stand about 3 feet behind you. Have her snap her fingers randomly around the back and sides of your head. Your job is to point to the snap, based only on sound, each time.
Most people do really well at this exercise. Your auditory system uses several types of information for this kind of task, including the time-level difference between the snap waveform hitting your left and right ears, that is — phase. After more than a century of work on this issue, researchers still have a lot to learn about how humans localize sound. There are many important practical applications for this question, including the need to produce better hearing aids and communication systems (military and commercial) that preserve localization information in noisy environments.
A promising new avenue of development for sound localization technology is the microphone array, where systems for extracting voice can be built by setting up a series of closely spaced microphones that pick up different phase patterns. This allows the system to provide better spatial audio and in some cases reconstruct “virtual” microphones to accept or reject certain sounds. In this way, voicing input in noisy environments can sometimes be boosted — a big problem for people with hearing aids.
Harmonizing with harmonics
The basic opening and closing gestures of your vocal folds produce the fundamental frequency (F0) of phonation. If you were bionic and made of titanium, this is all you would produce. In such a case, your voice would have only a fundamental frequency, and you would sound, well, kind of creepy, like a tuning fork. Fortunately, your fleshy and muscular vocal folds produce more than just a fundamental frequency — they also produce harmonics, which are additional flutters timed with the fundamental frequency at numbered intervals. Harmonics are regions of energy at integer multiples of the fundamental frequency. They’re properties of the voicing source, not the filter.
Harmonics result whenever an imperfect body — like a rubber band, guitar string, clarinet reed, or vocal fold — vibrates. If you could look at one such cycle, slowed down, with Superman’s eyes, you’d see that there’s not only a basic (or fundamental) vibration, but also there’s a whole series of smaller flutters that are timed with the basic vibration. These vibrations are smaller in amplitude, and (here is the amazing thing) they’re spaced in frequency by whole numbers. So, if you’re a guy and your fundamental frequency is 130 Hz (also known as your first harmonic), then your second harmonic would be 260 Hz, your third harmonic 390, and so forth. For a female with a higher fundamental frequency, say at 240 Hz, the second harmonic would be 480 Hz, the third 720, and so on. Harmonics are found throughout the speech frequency range (20 to 20,000 Hz). However, there’s more energy in the lower frequencies than in the higher because of a 12 dB per octave cutoff.
Extreme harmonics: Phonetics at the edge
A favorite classroom demonstration of mine is to take an enormous strip of rubber from a tire inner tube and stretch it across a phonetics class. Somebody grabs the middle of the inner tube strip and pulls it across to one side of the classroom, everybody ducks, and then the strip is released. As the strip zings back and forth, a few things visibly happen:
Students can clearly see the fundamental frequency (F0) of the band as it flies back and forth.
The band wobbles, showing the harmonics — sub-periodic oscillations that occur at whole number multiples of the fundamental frequency.
Everyone begins to laugh nervously because (after all) they haven’t been hit by the giant, dangerous piece of rubber.
A few students discreetly call their parents or attorneys.
This is the way of nature — you set up a simple harmonic series. Each harmonic series includes a fundamental frequency (or first harmonic) and an array of harmonics that have the relations times 2, times 3, times 4, and so on. Figure 12-6 shows these relations on a vibrating string.
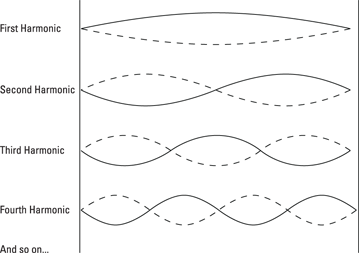
Illustration by Wiley, Composition Services Graphics
Figure 12-6: Harmonic series on a vibrating string.
This spectrum of fundamental frequency plus harmonics gives much of the warmth and richness to the human voice, something in the music world that makes up timbre (tone color or tone quality).
Resonating (Ommmm)
Producing voicing is half the story. After you’ve created a voiced source, you need to shape it. Acoustically, this shaping creates a condition called resonance, strengthening of certain aspects of sound and weakening of others. Resonance occurs when a sound source is passed through a structure.
Think about honking your car horn in a tunnel — the sound will carry because the shape of a tunnel boosts it. This kind of resonance occurs as a natural property of physical bodies. Big structures boost low sounds, small structures boost high sounds, and complex-shaped structures may produce different sound qualities.
Think of the shapes of musical instruments in a symphony — most of what you see has to do with resonance. The tube of a saxophone and the bell of a trumpet exist to shape sound, as does the body of a cello.
The parts of your body above the vocal folds (the lips, tongue, jaw, velum, nose, and throat) are able to form complicated passageway shapes that change with time. These shape changes have a cookie-cutter effect on your spectral source, allowing certain frequencies to be boosted and others to be dampened or suppressed. Figure 12-7 shows how this works acoustically during the production of three vowels, /i/, /ɑ/, and /u/.
Imagine that a crazed phonetician somehow places a microphone down at the level of your larynx just as you make each vowel. There would be only a neutral vibratory source (sounding something like an /ǝ/) for all three. The result would be a spectrum like the one at the bottom of Figure 12-7. Notice that this spectrum has a fundamental frequency and harmonics, as you might expect. When the vocal tract is positioned into different shapes for the three vowels (shown in the middle row of the figure), this has the effect of strengthening certain frequency areas and weakening others. This is resonance. By the time speech finally comes out the mouth, the acoustic picture is complex (as shown in the top of Figure 12-7). You can still see the fundamental frequency and harmonics of the source; however, there are also broad peaks. These are formants, labeled F1, F2, and F3.
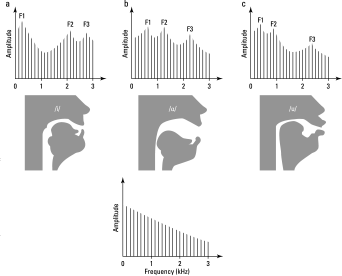
Illustration by Wiley, Composition Services Graphics
Figure 12-7: Acoustics from line plots of source (bottom), to resonance (middle), to output radiated spectra (top) for /i/ (a), /ɑ/ (b), and /u/ (c).
Formalizing formants
These F1, F2, and F3 peaks, called formant frequencies, are important acoustic landmarks for vowels and consonants. F1 is the lowest in frequency (shown on the horizontal axis of Figure 12-7, top), F2 is the middle, and F3 is the highest. Phoneticians identify these peaks in speech analysis programs, especially representations called the sound spectrogram (one of the most important visual representations of speech sound). Chapter 13 goes into sound spectography in detail. Although usually up to about four to five formants can be seen within the range of most speech analyses, the first three formants are the most important for speech.
Formants provide important information for both vowels and consonants. For vowels, listeners tune in to the relative positions of the first three formant frequencies as cues to typical vowel qualities. Tables 12-1 and 12-2 show values from our laboratory for vowel formant frequencies typical of men and child speakers of American English recorded in Dallas, Texas. Each table has underlined values, which I discuss in greater depth in the “Relating Sound to Mouth” section later in this chapter.
Formant frequency values are commonly used to classify vowels — for instance, in an F1 x F2 plot (refer to Figure 12-8). In this figure, you see that F1 is very similar to what you think of as tongue height and F2 as tongue advancement. This is a famous plot from research done by Gordon Peterson and Harold Barney in 1952 at Bell Laboratories (Murray Hill, New Jersey). It shows that vowels spoken by speakers of American English (shown by the phonetic characters in the ellipses) occupy their own positions in F1 x F2 space — although there is some overlap. For example, /i/ vowels occupy the most upper-left ellipse, while /ɔ/ vowels occupy the most lower-right ellipse. These findings show that tongue height and advancement play an important role in defining the vowels of American English.
Illustration by Wiley, Composition Services Graphics
Figure 12-8: F2 x F1 plot — American English vowels.
Formants also provide important information to listeners about consonants. For such clues, formants move — they lengthen, curve, shorten, and in general, keep phoneticians busy for years.
Here are some important points about formants:
Formants are important information sources for both vowels and consonants.
Formants are also known as resonant peaks.
Formants are properties of the filter (the vocal tract, throat, nose, and so on), not the vocal folds and larynx.
Formants are typically tracked on a sound spectrogram.
Tracking formants isn’t always that easy. In fact, scientists point out formants really can’t be measured, but are instead estimated.
A good way to keep in mind the three most important articulatory (and acoustic) properties of vowels is to keep it funny . . . as in, HAR HAR HAR:
H: Height relates inversely to F1.
A: Advancement relates to F2.
R: Rounding is a function of lip protrusion and lowers all formants through lengthening of the vocal tract by approximately 2 to 2.5 cm.
Relating Sound to Mouth
Don’t lose track of how practical and useful the information in this chapter can be to the speech language pathologist, actor, singer, or anyone else who wants to apply acoustic phonetics to his job, practice, or hobby. Because the basic relations between speech movements and speech acoustics are worked out, people can use this information for many useful purposes. For instance, look at these examples:
Clinicians may be able to determine whether their patients’ speech is typical or whether, say, the tongue is excessively fronted or lowered for a given sound.
An actor or actress may be able to compare his or her impression of an accent with established norms and adjust accordingly.
A second-language learner can be guided to produce English vowels in various computer games that give feedback based on microphone input.
The physics that cause these F1 to F3 rules are rather interesting and complex. You can think of your vocal tract as a closed tube, a bit like a paper-towel tube closed off at one end. In the human case, the open end is the mouth, and the closed end is the glottis. Such a tube naturally has three prominent formants, as shown in Figure 12-9. It’s a nice start, but the cavity resonance of the open mouth modifies these three resonances, and the articulators affect the whole system, which changes the shape of the tube. In this way, the vocal tract is rather like a wine bottle, where the key factor is the shape and size of the bottle itself (the chamber), the length of the neck, and the opening of the bottle (the mouth).
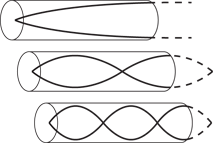
Illustration by Wiley, Composition Services Graphics
Figure 12-9: Closed-tube model of the vocal tract, showing first three resonances (formants).
In the case of your vocal tract (and not the wine bottle), chambers can move and change shape. So sometimes the front part of your chamber is big and the back is small, and other times vice versa. This can make the acoustics all a bit topsy-turvy — fortunately, there are some simple principles one can follow to keep track of everything.
The following sections take a closer look at these three rules and give you some pronunciation exercises to help you understand them. The purpose is to show how formant frequency (acoustic) information can be related to the positions of the tongue, jaw, and lips.
The F1 rule: Tongue height
The F1 rule is inversely related to tongue height, and the higher the tongue and jaw, the lower the frequency value of F1. Take a look at the underlined values in Table 12-1 (earlier in the chapter) to see how this works. The vowel /i/ (as in “bee”) is a high front vowel. Try saying it again, to be sure. You should feel your tongue at the high front of your mouth. This rule suggests that the F1 values should be relatively low in frequency. If you check Table 12-1 for the average value of adult males, you see it’s 300 Hz. Now produce /ɑ/, as in “father.” The F1 is 754 Hz, much higher in value. The inverse rule works: The lower the tongue, the higher the F1.
The F2 rule: Tongue fronting
The F2 rule states that the more front the tongue is placed, the higher the F2 frequency value. The (underlined) child value for /i/ of 2588 Hz is higher than that of /u/ as in “boot” at 1755 Hz.
The F3 rule: R-coloring
The F3 rule is especially important for distinguishing liquid sounds, also known as r and l. It turns out that every time an r-colored sound is made, F3 decreases in value. (R-coloring is when a vowel has an “r”-like quality; check out Chapter 7.) Compare, for instance, the value of male F3 in /ʌ/ as in “bug” and /ɝ/ as in “herd.” These values are 2539 Hz and 1686 Hz, respectively.
The F1–F3 lowering rule: Lip protrusion
The F1–F3 lowering rule is perhaps the easiest to understand in terms of its physics. It’s like a slide trombone: When the trombonist pushes out the slide, that plumbing gets longer and the sound goes down. It is the same thing with lip protrusion. The effect of protruding your lips is to make your vocal tract (approximately 17 cm long for males and 14 cm for females) about 2.5 cm longer. This will make all the resonant peaks go slightly lower.
Depending on the language, listeners hear this in different ways. For English speakers, it’s part of the /u/ and /ʊ/ vowels, such as in the words “suit” and “put.” Lip rounding also plays a role in English /ɔ/ and /o/, as in the words “law” and “hope.” In languages with phonemic lip rounding, such as French, Swedish, and German, it distinguishes word meaning by lowering sound.