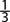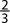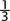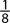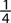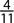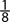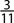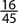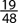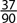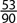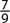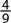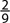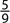chapter 1
Basic Concepts
Probability can be defined as the mathematics of chance. Most people are familiar with some aspects of probability by observing or playing gambling games such as lotteries, slot machines, blackjack, or roulette. However, probability theory is used in many other areas such as business, insurance, weather forecasting, and in everyday life.
In this chapter, you will learn about the basic concepts of probability using various devices such as coins, cards, and dice. These devices are not used as examples in order to make you an astute gambler, but they are used because they will help you understand the concepts of probability.
CHAPTER OBJECTIVES
In this chapter, you will learn
• The basic concepts of probability including probability experiments, sample spaces, simple and compound events, and equally likely events
• How to find the probability of an event using the classical probability formula
• How to find the probability of an event using a frequency distribution
• The range of probability values
• The basic probability rules
• How to find the probability of a complement of an event
• The law of large numbers
• The concept of subjective probability
Probability Experiments
Chance processes, such as flipping a coin, rolling a die (singular for dice), or drawing a card at random from a well-shuffled deck are called probability experiments. A probability experiment is a chance process that leads to well-defined outcomes or results. For example, tossing a coin can be considered a probability experiment since there are two well-defined outcomes—heads and tails.
An outcome of a probability experiment is the result of a single trial of a probability experiment. A trial means flipping a coin once or drawing a single card from a deck. A trial could also mean rolling two dice at once, tossing three coins at once, or drawing five cards from a deck at once. A single trial of a probability experiment means to perform the experiment one time.
The set of all outcomes of a probability experiment is called a sample space. Some sample spaces for various probability experiments are shown here.
Experiment |
Sample Space |
Toss one coin |
H, T* |
Roll a die |
1, 2, 3, 4, 5, 6 |
Toss two coins |
HH, HT, TH, TT |
*H = heads; T = tails |
Notice that when two coins are tossed, there are four outcomes, not three. Consider tossing a nickel and a dime at the same time. Both coins could fall heads up. Both coins could fall tails up. The nickel could fall heads up and the dime could fall tails up, or the nickel could fall tails up and the dime could fall heads up. The situation is the same even if the coins are indistinguishable.
It should be mentioned that each outcome of a probability experiment occurs at random. This means you cannot predict with certainty which outcome will occur when the experiment is conducted. Also, each outcome of the experiment is equally likely unless otherwise stated. That means that each outcome has the same probability of occurring.
When finding probabilities, it is often necessary to consider several outcomes of the experiment. For example, when a single die is rolled, you may want to consider obtaining an even number; that is, a 2, 4, or 6. This is called an event. An event then consists of one or more outcomes of a probability experiment.
NOTE It is sometimes necessary to consider an event which has no outcomes. This will be explained later.
An event with one outcome is called a simple event. For example, a die is rolled and the event of getting a 4 is a simple event since there is only one way to get a 4. When an event consists of two or more outcomes, it is called a compound event. For example, if a die is rolled and the event is getting an odd number, the event is a compound event since there are three ways to get an odd number, namely, 1, 3, or 5.
Simple and compound events should not be confused with the number of times the experiment is repeated. For instance, if two coins are tossed, the event of getting two heads is a simple event since there is only one way to get two heads, whereas the event of getting a head and a tail in either order is a compound event since it consists of two outcomes, namely, head, tail and tail, head.
EXAMPLE
__________________________________________________
A single die is rolled. List the outcomes in each event:
a. Getting an even number
b. Getting a number greater than 3
c. Getting less than 1
SOLUTION
__________________________________________________
a. The event contains the outcomes of 2, 4, and 6
b. The event contains the outcomes of 4, 5, and 6
c. When you roll a die, you cannot get a number less than 1; hence, the event contains no outcomes
 Still Struggling
Still Struggling
Remember, when finding the outcomes in the sample space, be sure to include all the outcomes. For example, when two coins are tossed, there are four outcomes, not three, since there are two ways to get a head and a tail: HT and TH.
Classical Probability
Sample spaces are used in classical probability to determine the numerical probability that an event will occur. The formula for determining the probability of an event E is
EXAMPLE
__________________________________________________
Two coins are tossed; find the probability that both coins land tails up.
SOLUTION
__________________________________________________
The sample space for tossing two coins is HH, HT, TH, and TT. Since there are four events in the sample space, and only one way to get two tails (TT), the answer is
EXAMPLE
__________________________________________________
A die is tossed; find the probability of each event:
a. Getting a 5
b. Getting an odd number
c. Getting a number less than 4
SOLUTION
__________________________________________________
The sample space is 1, 2, 3, 4, 5, 6, so there are six outcomes in the sample space.
a. P(5) =  , since there is only 1 way to obtain a 5
, since there is only 1 way to obtain a 5
b. P(odd number) 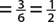 , since there are 3 ways to get an odd number, 1, 3, or 5
, since there are 3 ways to get an odd number, 1, 3, or 5
c. P(number less than 4) 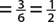 , since there are 3 numbers in the sample
space less than 4
, since there are 3 numbers in the sample
space less than 4
EXAMPLE
__________________________________________________
A dish contains six red jellybeans, four yellow jellybeans, two black jellybeans, and three pink jellybeans. If a jellybean is selected at random, find the probability that it is
a. A pink jellybean
b. A yellow or black jellybean
c. Not a red jellybean
d. A blue jellybean
SOLUTION
__________________________________________________
There are 6 + 4 + 2 + 3 = 15 outcomes in the sample space.
a. P(pink) 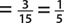
b. P(yellow or black) 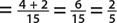
c. P(not red) = P(yellow or black or pink) 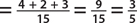
d. P(blue) 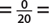 0, since there are no blue jellybeans
0, since there are no blue jellybeans
Probabilities can be expressed as reduced fractions, decimals, or percents. For example, if a coin is tossed, the probability of getting heads up is  or 0.5 or 50%.
or 0.5 or 50%.
NOTE Some mathematicians feel that probabilities should be expressed only as fractions or decimals. However, probabilities are often given as percents in everyday life. For example, one often hears, “There is a 50% chance that it will rain tomorrow.”
Probability problems use a certain language. For example, suppose a die is tossed. An event that is specified as “getting at least a 3” means getting a 3, 4, 5, or 6. An event that is specified as “getting at most a 3” means getting a 1, 2, or 3.
Probability Rules
There are certain rules that apply to classical probability theory. They are presented next.
Rule 1: The probability of any event will always be a number from 0 to 1.
This can be denoted mathematically as 0 ≤ P(E) ≥ 1. What this means is that all answers to probability problems will be a number ranging from 0 to 1. Probabilities cannot be negative nor can they be greater than one.
Also, when the probability of an event is close to zero, the occurrence of the event is relatively unlikely. For example, if the chances that you will win a certain lottery are 0.001 or 1 in 1000, you probably won’t win, unless of course, you are very “lucky.” When the probability of an event is 0.5 or  , there is a 50-50 chance that the event will happen—the same probability of getting one of the two outcomes when flipping a coin. When the probability of an event is close to one, the event is almost certain to occur. For example, if the chance of it snowing tomorrow is 90%, more than likely you’ll see some snow. See Figure 1-1.
, there is a 50-50 chance that the event will happen—the same probability of getting one of the two outcomes when flipping a coin. When the probability of an event is close to one, the event is almost certain to occur. For example, if the chance of it snowing tomorrow is 90%, more than likely you’ll see some snow. See Figure 1-1.
Rule 2: When an event cannot occur, the probability will be 0.
EXAMPLE
__________________________________________________
A die is rolled; find the probability of getting a 7.
SOLUTION
__________________________________________________
Since the sample space is 1, 2, 3, 4, 5, and 6, and there is no way to get a 7, P(7) = 0. The event in this case has no outcomes which are contained in the sample space.
Rule 3: When an event is certain to occur, the probability is 1.
EXAMPLE
__________________________________________________
A die is rolled; find the probability of getting a number less than 7.
SOLUTION
__________________________________________________
Since all outcomes in the sample space are less than 7, the probability is  .
.
Rule 4: The sum of the probabilities of all of the outcomes in the sample space is 1.
Refer to the sample space for tossing two coins (HH, HT, TH, TT): Each outcome has a probability of  , and the sum of the probabilities of all of the outcomes is
, and the sum of the probabilities of all of the outcomes is 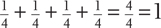 .
.
Rule 5: The probability that an event will not occur is equal to 1 minus the probability that the event will occur.
For example, when a die is rolled, the sample space is 1, 2, 3, 4, 5, 6. Now consider the event E of getting a number less than 3. This event consists of the outcomes 1 and 2. The probability of event E is P(E) 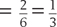 . The outcomes in which E will not occur are 3, 4, 5, and 6, so the probability that event E will not occur is
. The outcomes in which E will not occur are 3, 4, 5, and 6, so the probability that event E will not occur is  . The answer to P(not E) = 1 – P(E)
. The answer to P(not E) = 1 – P(E)  .
.
If an event E consists of certain outcomes, then event  (E bar) is called the complement of event E and consists of the outcomes in the sample space which are not outcomes of event E. In the previous situation, the outcomes in E are 1 and 2. Therefore, the outcomes in
(E bar) is called the complement of event E and consists of the outcomes in the sample space which are not outcomes of event E. In the previous situation, the outcomes in E are 1 and 2. Therefore, the outcomes in  are 3, 4, 5, and 6. Now Rule 5 can be stated mathematically as
are 3, 4, 5, and 6. Now Rule 5 can be stated mathematically as  = 1 – P(E).
= 1 – P(E).
EXAMPLE
__________________________________________________
If the chance of rain is 0.40 (40%), find the probability that it won’t rain.
SOLUTION
__________________________________________________
Since P(E) = 0.40 and P ( ) = 1 – P(E), then the probability that it won’t rain is 1 – 0.40 = 0.60 or 60%. Hence the probability that it won’t rain is 60%.
) = 1 – P(E), then the probability that it won’t rain is 1 – 0.40 = 0.60 or 60%. Hence the probability that it won’t rain is 60%.
 Still Struggling
Still Struggling
Even though an event cannot occur, we still can assign a probability value mathematically. It is 0.
PRACTICE
__________________________________________________
1. A single die is rolled. Find each probability:
a. The number shown on the face is a 4.
b. The number shown on the face is less than 3.
c. The number shown on the face is less than 1.
d. The number shown on the face is divisible by 3.
2. A box contains a $1 bill, a $2 bill, a $5 bill, a $10 bill, and a $20 bill. A person selects a bill at random. Find each probability:
a. The bill selected is a $2 bill.
b. The denomination of the bill selected is more than $5.
c. The bill selected is a $100 bill.
d. The bill selected is of an even denomination.
e. The denomination of the bill is divisible by 10.
3. Two coins are tossed. Find each probability:
a. Getting two heads.
b. Getting at least one tail.
c. Getting two tails.
4. The cards A♥, 2♦ , 3♣, 4♥, 5♠, and 6♣ are shuffled and dealt face down on a table. (Hearts and diamonds are red; clubs and spades are black.) If a person selects one card at random, find the probability that the card is
a. The ace of hearts.
b. A black card.
c. A spade.
5. A spinner for a child’s game has the numbers 1 through 5 evenly spaced. If a child spins, find each probability:
a. The number is divisible by 2.
b. The number is greater than 6.
c. The number is an odd number.
6. A letter is randomly selected from the word “calculator.” Find the probability that the letter is
a. A “u”.
b. An “a”.
c. A “c” or an “l”.
d. A vowel.
7. There are four women and five men employed in a real estate office. If a person is selected at random to get lunch for the group, find the probability that the person is a woman.
8. A marble is selected at random from a bag containing two red marbles, one blue marble, three green marbles, and one white marble. Find the probability that the ball is
a. A green marble.
b. A red or a blue marble.
c. An orange marble.
9. On a roulette wheel there are 38 sectors. Eighteen are red, 18 are black, and two are green. When the wheel is spun, find the probability that the ball will land on
a. Black.
b. Green.
10. A person has a penny, a nickel, a dime, a quarter, and a half-dollar in his pocket. If a coin is selected at random, find the probability that the coin is
a. A nickel.
b. A coin whose amount is greater than 10 cents.
c. A coin whose denomination ends in a 0.
ANSWERS
__________________________________________________
1. The sample space is 1, 2, 3, 4, 5, 6.
a. P(4) 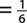 , since there is only one 4 in the sample space.
, since there is only one 4 in the sample space.
b. P(number less than 3) 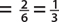 , since there are 2 numbers in the sample space less than 3.
, since there are 2 numbers in the sample space less than 3.
c. P(number less than 1) 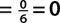 , since there are no numbers in the sample space less than 1.
, since there are no numbers in the sample space less than 1.
d. P(number is divisible by 3)  , since 3 and 6 are divisible by 3.
, since 3 and 6 are divisible by 3.
2. The sample space is $1, $2, $5, $10, $20.
a. P($2) 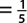 .
.
b. P(bill greater than $5) 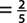 , since $10 and $20 are greater than $5.
, since $10 and $20 are greater than $5.
c. P($100) 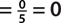 , since there is no $100 bill in the sample space.
, since there is no $100 bill in the sample space.
d. P(bill is even)  , since $2, $10, and $20 are even denomination bills.
, since $2, $10, and $20 are even denomination bills.
e. P(number is divisible by 10) 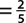 , since $10 and $20 are divisible by 10.
, since $10 and $20 are divisible by 10.
3. The sample space is HH, HT, TH, TT.
a. P(HH) 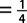 , since there is only 1 way to get 2 heads.
, since there is only 1 way to get 2 heads.
b. P(at least one tail) 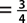 , since there are 3 ways (HT, TH, TT) to get at least 1 tail.
, since there are 3 ways (HT, TH, TT) to get at least 1 tail.
c. P(TT)  , since there is only 1 way to get 2 tails.
, since there is only 1 way to get 2 tails.
4. The sample space is A♥, 2♦, 3♣, 4♥, 5♠, 6♣.
a. P(ace of hearts) 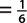 .
.
b. P(black card) 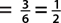 , since there are 3 black cards.
, since there are 3 black cards.
c. P(spade)  , since there is 1 spade.
, since there is 1 spade.
5. The sample space is 1, 2, 3, 4, 5.
a. P(number divisible by 2) 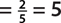 , since 2 and 4 are divisible by 2.
, since 2 and 4 are divisible by 2.
b. P(number greater than 6) 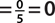 , since no numbers are greater than 6.
, since no numbers are greater than 6.
c. P(odd number)  , since 1, 3, and 5 are odd numbers.
, since 1, 3, and 5 are odd numbers.
6. The sample space consists of the letters in “calculator.”
a. P(u)  .
.
b. P(a)  .
.
c. P(c or l) 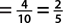 .
.
d. P(vowel)  , since a, u, and o are vowels.
, since a, u, and o are vowels.
7. The sample space consists of four women and five men. P(woman) 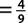 .
.
8. The sample space is red, red, blue, green, green, green, and white.
a. P(green) 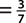 , since there are 3 green marbles.
, since there are 3 green marbles.
b. P(red or blue) 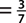 , since there are 2 red marbles and 1 blue marble.
, since there are 2 red marbles and 1 blue marble.
c. P(orange)  , since there are no orange marbles.
, since there are no orange marbles.
9. There are 38 outcomes.
a. P(black) 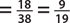 .
.
b. P(green) 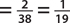 .
.
10. The sample space is 1 , 5
, 5 , 10
, 10 , 25
, 25 , 50
, 50 .
.
a. P(5 )
)  .
.
b. P(greater than 10 )
)  .
.
c. P(denomination ends in 0)  .
.
Empirical Probability
Probabilities can be computed for situations that do not use sample spaces. In these cases, frequency distributions are used and the probability is called empirical probability. For example, suppose a class of students consists of six freshmen, two sophomores, 10 juniors, and 12 seniors. The information can be summarized in a frequency distribution as follows:
Rank |
Frequency |
Freshmen |
6 |
Sophomores |
2 |
Juniors |
10 |
Seniors |
12 |
TOTAL |
30 |
From a frequency distribution, probabilities can be computed using the formula
Empirical probability is sometimes called relative frequency probability.
EXAMPLE
__________________________________________________
Using the frequency distribution shown previously, find the probability of selecting a senior student at random.
SOLUTION
__________________________________________________
Since there are 12 seniors and a total of 30 students, P(senior) 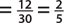 .
.
Another aspect of empirical probability is that if a large number of subjects (called a sample) is selected from a particular group (called a population), and the probability of a specific attribute is computed, then when another subject is selected, we can say the probability that this subject has the same attribute is the same as the original probability computed for the group. For example, a Gallup Poll of 1004 adults surveyed found that 17% of the subjects stated that they considered Abraham Lincoln to be the greatest President of the United States. Now if a subject is selected, the probability that he or she will say President Lincoln is the greatest president is 17%.
Several things should be explained here. First of all, the 1004 people constituted a sample selected from a larger group called the population. Second, the exact probability for the population can never be known unless every single member of the population is surveyed. This does not happen in these kinds of surveys because the population is usually very large. Hence, the 17% is only an estimate of the probability. However, if the sample is representative of the population, the estimate will usually be fairly close to the exact probability. Statisticians have a way of computing the accuracy (called the margin of error) for these situations. For the present, we shall just concentrate on the probability.
Also, by a representative sample, we mean the subjects of the sample have similar characteristics as those in the population. There are statistical methods to help the statisticians obtain a representative sample. These methods are called sampling methods and can be found in many statistics books.
EXAMPLE
__________________________________________________
The same study found 7% considered George Washington to be the greatest president. If a person is selected at random, find the probability that he or she considers George Washington to be the greatest president.
SOLUTION
__________________________________________________
The probability is 7%.
EXAMPLE
__________________________________________________
In a sample of 832 people over 30 years of age, 180 had a bachelor’s degree. If a person over 30 years of age is selected, find the probability that the person has a bachelor’s degree.
SOLUTION
__________________________________________________
In this case,
P(bachelor’s degree)  (rounded) or about 21.6%.
(rounded) or about 21.6%.
EXAMPLE
__________________________________________________
In the sample study of 832 people, it was found that 680 people have a high school diploma. If a person is selected at random, find the probability that the person does not have a high school diploma.
SOLUTION
__________________________________________________
The probability that a person has a high school diploma is
Hence, the probability that a person does not have a high school diploma is
P(no high school diploma) = 1 – P(high school diploma)
= 1 – 0.817 = 0.183 = 18.3%
Alternate Solution:
If 680 people have a high school diploma, then 832 – 680 = 152 do not have a high school diploma. Hence,
Consider another aspect of probability. Suppose a baseball player has a batting average of 0.250. What is the probability that he will get a hit the next time he gets to bat? Although we cannot be sure of the exact probability, we can use 0.250 as an estimate. Since 0.250  , we can say that there is a one in four chance that he will get a hit the next time he bats.
, we can say that there is a one in four chance that he will get a hit the next time he bats.
 Still Struggling
Still Struggling
When the probability of an event is expressed as a fraction with a large denominator, it might be more meaningful to represent it as a decimal or percent.
PRACTICE
__________________________________________________
1. In a sample of 60 people, 18 had type O blood, 32 had type A blood, 7 had type B blood, and 3 had type AB blood. If a person is selected at random, find the probability that the person
a. Has type B blood
b. Has type B or type AB blood
c. Does not have type A blood
d. Has neither type AB nor type O blood
2. In a recent survey of 425 children ages 6 to 8 years, it was found that 132 did not like to go to school. If a child is selected at random, find the probability that he or she did not like to go to school.
3. A recent survey found that the ages of nurses in a hospital network is distributed as follows:
Age |
Number |
20–29 |
10 |
30–39 |
36 |
40–49 |
22 |
50–59 |
18 |
60 or older |
14 |
|
100 |
If a person is selected at random, find the probability that the person is
a. 50 or older
b. Under 30 years old
c. Between 40 and 59 years old
d. Under 60 but over 29 years old
4. A recent survey found that 64% of those questioned get some of the news from the Internet. If a person is selected at random, find the probability that the person does not get any news from the Internet.
5. In a classroom of 32 students, 12 were liberal arts majors and 18 were history majors. If a student is selected at random, find the probability that the student is neither a liberal arts major nor a history major.
ANSWERS
__________________________________________________
1. The total number of outcomes in this sample space is 60.
a. P(B) 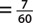
b. P(B or AB) 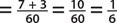
c. P(not A) 
d. P(neither AB nor O) = P(A or B) 
2. P(not like school) 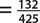
3. a. P(50 or older) 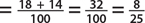
b. P(under 30) 
c. P(between 40 and 59) 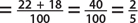
d. P(over 29 but under 60) 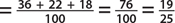
4. P(no news from Internet) = 1 – 0.64 = 0.36
5. P(no news from Internet) 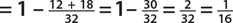
Law of Large Numbers
We know from classical probability that if a coin is tossed one time, we cannot predict the outcome, but the probability of getting a head is  and the probability of getting a tail is
and the probability of getting a tail is  if everything is fair. But what happens if we toss the coin 100 times? Will we get 50 heads? Common sense tells us that most of the time, we will not get exactly 50 heads, but we should get close to 50 heads. What will happen if we toss a coin 1000 times? Will we get exactly 500 heads? Probably not. However, as the number of heads increases, the ratio of the number of heads to the total number of tosses will get closer to
if everything is fair. But what happens if we toss the coin 100 times? Will we get 50 heads? Common sense tells us that most of the time, we will not get exactly 50 heads, but we should get close to 50 heads. What will happen if we toss a coin 1000 times? Will we get exactly 500 heads? Probably not. However, as the number of heads increases, the ratio of the number of heads to the total number of tosses will get closer to  . This phenomenon is known as the law of large numbers. This law holds for any type of gambling game such as rolling dice, playing roulette, etc.
. This phenomenon is known as the law of large numbers. This law holds for any type of gambling game such as rolling dice, playing roulette, etc.
Subjective Probability
A third type of probability is called subjective probability. Subjective probability is based upon an educated guess, estimate, opinion, or inexact information. For example, a sports writer may say that there is a 60% probability that the Pittsburgh Steelers will be in the Super Bowl next year. Here the sports writer is basing his opinion on subjective information such as the relative strength of the Steelers, their opponents, their coach, etc. Two individuals’ estimates of subjective probability can be different since each person would have different information about the situation. For example, a union president might guess the probability of the employees going on strike at 80%, whereas the owner of the company might say it would be 60%. Each person could be getting information from different sources. Subjective probabilities are used in everyday life; however, they are beyond the scope of this book.

PROBABILITY SIDELIGHT: Brief History of Probability
The concepts of probability are as old as humans. Paintings in tombs excavated in Egypt showed that people played games based on chance as early as 1800 BCE.
One game was called “Hounds and Jackals” and is similar to the present-day game of “Snakes and Ladders.”
Ancient Greeks and Romans made crude dice from various items such as animal bones, stones, and ivory. When some of these items were tested recently, they
were found to be quite accurate. These crude dice were also used in fortune telling
and divination.
Emperor Claudius (10 BCE–54 CE) is said to have written a book entitled How To Win at Dice. He liked to play so much that he had a special dice board in his carriage.
No formal study of probability was done until the 16th century when Girolamo Cardano (1501–1576) wrote a book on probability entitled The Book on Chance and Games. Cardano was a philosopher, astrologer, physician, mathematician, and gambler. In his book, he also included techniques on how to cheat and how to catch others who are cheating. He is believed to be the first mathematician to formulate a definition of classical probability.
During the mid-1600s, a professional gambler named Chevalier de Mere made a considerable amount of money on a gambling game. He would bet unsuspecting patrons that in four rolls of a die, he could obtain at least one 6. He was so successful at winning that word got around, and people refused to play. He decided to invent a new game in order to keep winning. He would bet patrons that if he rolled two dice 24 times, he would get at least one double 6. However, to his dismay, he began to lose more often than he would
win.
Unable to figure out why he was losing, he asked a renowned mathematician, Blaise Pascal (1623–1662) to study the game. Pascal was a child prodigy when it came to mathematics. At the age of 14, he participated in weekly meetings of the mathematicians of the French Academy. At the age of 16, he invented a mechanical adding machine.
Because of the dice problem, Pascal became interested in studying probability and began a correspondence with a French government official and fellow mathematician, Pierre de Fermat (1601–1665). Together the two were able to solve de Mere’s dilemma and formulate the beginnings of probability theory.
In 1657, a Dutch mathematician named Christian Huygens wrote a treatise on the Pascal–Fermat correspondence and introduced the idea of mathematical expectation. (See Chapter 5.)
Abraham de Moivre (1667–1754) wrote a book on probability entitled Doctrine of Chances in 1718. He published a second edition in 1738.
Pierre Simon Laplace (1749–1827) wrote a book and a series of supplements on probability from 1812 to 1825. His purpose was to acquaint readers with the theory of probability and its applications using everyday language. He also stated that the probability that the sun will rise tomorrow is  .
.
Simeon-Denis Poisson (1781–1840) developed the concept of the Poisson distribution. (See Chapter 8.)
Also during the 1800s, a mathematician named Carl Friedrich Gauss (1777–1855) developed the concepts of the normal distribution. Earlier work on the normal distribution was also done by DeMoivre and Laplace, unknown to Gauss. (See Chapter 9.)
In 1895, the Fey Manufacturing Company of San Francisco invented the first automatic slot machine. These machines consisted of three wheels that were spun when a handle on the side of the machine was pulled. Each wheel contained 20 symbols; however, the number of the same symbols was not the same on each wheel. For example, the first wheel may have 6 oranges, while the second wheel has 3 oranges, and the third wheel has 1 orange. When a person gets two oranges, the person may think that he has almost won by getting 2 out of 3 equitable symbols when the real probability of winning is much smaller.
In the late 1940s, two mathematicians, John von Neumann and Stanislaw Ulam, used a computer to simulate probability experiments. This method is called the Monte Carlo method. (See Chapter 10.)
Today probability theory is used in insurance, gambling, war gaming, the stock market, weather predicting, and many other areas.

Summary
Probability is the mathematics of chance. There are three types of probability: classical probability, empirical probability, and subjective probability. Classical probability uses sample spaces. A sample space is the set of outcomes of a probability experiment. The range of probability is from 0 to 1. If an event cannot occur, its probability is 0. If an event is certain to occur, its probability is 1. Classical probability is defined as the number of ways (outcomes) the event can occur divided by the total number of outcomes in the sample space.
Empirical probability uses frequency distributions, and it is defined as the frequency of an event divided by the total number of frequencies.
Subjective probability is made by a person’s knowledge of the situation and is basically an educated guess as to the chances of an event occurring.
QUIZ
1. Rolling a die or tossing a coin is called a
A. Repeated experiment
B. Sample experiment
C. Probability experiment
D. Infinite experiment
2. Which is not a type of probability?
A. Subjective
B. Classical
C. Variable
D. Empirical
3. The range of the values a probability can assume is
A. From 0 to 1
B. From 1 to 100
C. From 0 to 
D. From –1 to +1
4. When an event cannot occur, its probability is
A. 
B. 0.01
C. 1
D. 0
5. The set of all possible outcomes of a probability experiment is called the
A. Outcome space
B. Sample space
C. Experimental space
D. Event space
6. How many outcomes are there altogether when three coins are tossed?
A. 1
B. 2
C. 4
D. 8
7. The type of probability that uses sample spaces is called
A. Subjective probability
B. Empirical probability
C. Classical probability
D. Relative probability
8. When an event is certain to occur, its probably is
A. –1
B. 
C. 0
D. 1
9. When two coins are tossed, the sample space is
A. H, T, HT
B. HH, HT, TT
C. H, T
D. HH, HT, TH, TT
10. When a die is rolled, the probability of getting a number greater than 2 is
A. 
B. 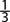
C. 
D. 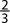
11. When two coins are tossed, the probability of getting two heads is
A. 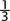
B. 
C. 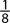
D. 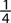
12. If a letter is selected at random from the word “Mississippi,” find the probability that it is an “i.”
A. 
B. 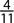
C. 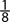
D. 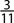
13. When a die is rolled, the probability of getting a 7 is
A. 0
B. 
C. 
D. 1
14. In a survey of 240 people, 95 were over the age of 62. If a person is selected at random, what is the probability that the person is over 62?
A. 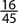
B. 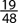
C. 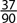
D. 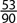
15. In a classroom of 27 students, there were 21 freshmen. If a student is selected at random, what is the probability that the student is not a freshman?
A. 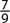
B. 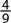
C. 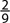
D. 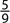






 Still Struggling
Still Struggling



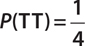



 , since there is only 1 way to obtain a 5
, since there is only 1 way to obtain a 5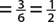 , since there are 3 ways to get an odd number, 1, 3, or 5
, since there are 3 ways to get an odd number, 1, 3, or 5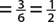 , since there are 3 numbers in the sample
space less than 4
, since there are 3 numbers in the sample
space less than 4


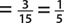
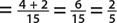
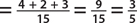
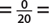 0, since there are no blue jellybeans
0, since there are no blue jellybeans
 or 0.5 or 50%.
or 0.5 or 50%.
 , there is a 50-50 chance that the event will happen—the same probability of getting one of the two outcomes when flipping a coin. When the probability of an event is close to one, the event is almost certain to occur. For example, if the chance of it snowing tomorrow is 90%, more than likely you’ll see some snow. See Figure 1-1.
, there is a 50-50 chance that the event will happen—the same probability of getting one of the two outcomes when flipping a coin. When the probability of an event is close to one, the event is almost certain to occur. For example, if the chance of it snowing tomorrow is 90%, more than likely you’ll see some snow. See Figure 1-1.





 .
.
 , and the sum of the probabilities of all of the outcomes is
, and the sum of the probabilities of all of the outcomes is 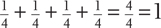 .
.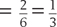 . The outcomes in which E will not occur are 3, 4, 5, and 6, so the probability that event E will not occur is
. The outcomes in which E will not occur are 3, 4, 5, and 6, so the probability that event E will not occur is  . The answer to P(not E) = 1 – P(E)
. The answer to P(not E) = 1 – P(E)  .
. (E bar) is called the complement of event E and consists of the outcomes in the sample space which are not outcomes of event E. In the previous situation, the outcomes in E are 1 and 2. Therefore, the outcomes in
(E bar) is called the complement of event E and consists of the outcomes in the sample space which are not outcomes of event E. In the previous situation, the outcomes in E are 1 and 2. Therefore, the outcomes in  are 3, 4, 5, and 6. Now Rule 5 can be stated mathematically as
are 3, 4, 5, and 6. Now Rule 5 can be stated mathematically as  = 1 – P(E).
= 1 – P(E).

 ) = 1 – P(E), then the probability that it won’t rain is 1 – 0.40 = 0.60 or 60%. Hence the probability that it won’t rain is 60%.
) = 1 – P(E), then the probability that it won’t rain is 1 – 0.40 = 0.60 or 60%. Hence the probability that it won’t rain is 60%.
 Still Struggling
Still Struggling

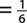 , since there is only one 4 in the sample space.
, since there is only one 4 in the sample space.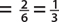 , since there are 2 numbers in the sample space less than 3.
, since there are 2 numbers in the sample space less than 3.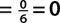 , since there are no numbers in the sample space less than 1.
, since there are no numbers in the sample space less than 1. , since 3 and 6 are divisible by 3.
, since 3 and 6 are divisible by 3.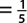 .
.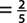 , since $10 and $20 are greater than $5.
, since $10 and $20 are greater than $5.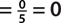 , since there is no $100 bill in the sample space.
, since there is no $100 bill in the sample space. , since $2, $10, and $20 are even denomination bills.
, since $2, $10, and $20 are even denomination bills.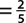 , since $10 and $20 are divisible by 10.
, since $10 and $20 are divisible by 10.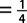 , since there is only 1 way to get 2 heads.
, since there is only 1 way to get 2 heads.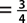 , since there are 3 ways (HT, TH, TT) to get at least 1 tail.
, since there are 3 ways (HT, TH, TT) to get at least 1 tail. , since there is only 1 way to get 2 tails.
, since there is only 1 way to get 2 tails.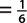 .
.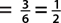 , since there are 3 black cards.
, since there are 3 black cards. , since there is 1 spade.
, since there is 1 spade.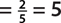 , since 2 and 4 are divisible by 2.
, since 2 and 4 are divisible by 2.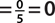 , since no numbers are greater than 6.
, since no numbers are greater than 6. , since 1, 3, and 5 are odd numbers.
, since 1, 3, and 5 are odd numbers. .
. .
.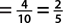 .
. , since a, u, and o are vowels.
, since a, u, and o are vowels.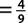 .
.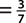 , since there are 3 green marbles.
, since there are 3 green marbles.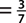 , since there are 2 red marbles and 1 blue marble.
, since there are 2 red marbles and 1 blue marble. , since there are no orange marbles.
, since there are no orange marbles.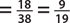 .
.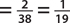 .
. , 5
, 5 , 10
, 10 , 25
, 25 , 50
, 50 .
. )
)  .
. )
)  .
. .
.




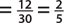 .
.





 (rounded) or about 21.6%.
(rounded) or about 21.6%.



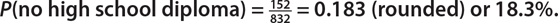
 , we can say that there is a one in four chance that he will get a hit the next time he bats.
, we can say that there is a one in four chance that he will get a hit the next time he bats.
 Still Struggling
Still Struggling

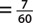
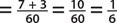


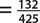
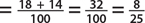

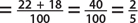
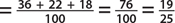
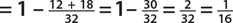


 and the probability of getting a tail is
and the probability of getting a tail is  if everything is fair. But what happens if we toss the coin 100 times? Will we get 50 heads? Common sense tells us that most of the time, we will not get exactly 50 heads, but we should get close to 50 heads. What will happen if we toss a coin 1000 times? Will we get exactly 500 heads? Probably not. However, as the number of heads increases, the ratio of the number of heads to the total number of tosses will get closer to
if everything is fair. But what happens if we toss the coin 100 times? Will we get 50 heads? Common sense tells us that most of the time, we will not get exactly 50 heads, but we should get close to 50 heads. What will happen if we toss a coin 1000 times? Will we get exactly 500 heads? Probably not. However, as the number of heads increases, the ratio of the number of heads to the total number of tosses will get closer to  . This phenomenon is known as the law of large numbers. This law holds for any type of gambling game such as rolling dice, playing roulette, etc.
. This phenomenon is known as the law of large numbers. This law holds for any type of gambling game such as rolling dice, playing roulette, etc.

 .
.