2 The Logic of Shape

First steps in geometry

There are two main types of reasoning in mathematics: symbolic and visual. Symbolic reasoning originated in number notation, and we will shortly see how it led to the invention of algebra, in which symbols can represent general numbers (‘the unknown’) rather than specific ones (‘7’). From the Middle Ages onwards, mathematics came to rely increasingly heavily on the use of symbols, as a glance at any modern mathematics text will confirm.

The beginnings of geometry

As well as symbols, mathematicians use diagrams, opening up various types of visual reasoning. Pictures are less formal than symbols, and their use has sometimes been frowned upon for that reason. There is a widespread feeling that a picture is somehow less rigorous, logically speaking, than a symbolic calculation. It is true that pictures leave more room for differences of interpretation than symbols. Additionally, pictures can contain hidden assumptions – we cannot draw a ‘general’ triangle; any triangle we draw has a particular size and shape, which may not be representative of an arbitrary triangle. Nonetheless, visual intuition is such a powerful feature of the human brain that pictures play a prominent role in mathematics. In fact, they introduce a second major concept into the subject, after number. Namely, shape.

Mathematicians’ fascination with shapes goes back a long way. There are diagrams on Babylonian tablets. For example, the tablet catalogued as YBC 7289 shows a square and two diagonals. The sides of the square are marked with cuneiform numerals for 30. Above one diagonal is marked 1;24,51,10, and below it 42;25,35, which is its product by 30 and therefore the length of that diagonal. So 1;24,51,10 is the length of the diagonal of a smaller square, with sides 1 unit. Pythagoras’s Theorem tells us that this diagonal is the square root of two, which we write as . The approximation 1;24,51,10 to is very good, correct to 6 decimal places.

Tablet YBC 7289 and its cuneiform numerals

The first systematic use of diagrams, together with a limited use of symbols and a heavy dose of logic, occurs in the geometric writings of Euclid of Alexandria. Euclid’s work followed a tradition that went back at least to the Pythagorean cult, which flourished around 500 BC, but Euclid insisted that any mathematical statement must be given a logical proof before it could be assumed to be true. So Euclid’s writings combine two distinct innovations: the use of pictures and the logical structure of proofs. For centuries, the word ‘geometry’ was closely associated with both.

In this chapter we follow the story of geometry from Pythagoras, through Euclid and his forerunner Eudoxus, to the late period of classical Greece and Euclid’s successors Archimedes and Apollonius. These early geometers paved the way for all later work on visual thinking in mathematics. They also set standards of logical proof that were not surpassed for millennia.

Pythagoras

Today we almost take it for granted that mathematics provides a key to the underlying laws of nature. The first recorded systematic thinking along those lines comes from the Pythagoreans, a rather mystical cult dating from roughly 600 BC to 400 BC. Its founder, Pythagoras, was born on Samos around 569 BC. When and where he died is a mystery, but in 460 BC the cult that he founded was attacked and destroyed, its meeting places wrecked and burned. In one, the house of Milo in Croton, more than 50 Pythagoreans were slaughtered. Many survivors fled to Thebes in Upper Egypt. Possibly Pythagoras was one of them, but even this is conjectural, for legends aside, we know virtually nothing about Pythagoras. His name is well known, mainly because of his celebrated theorem about right-angled triangles, but we don’t even know whether Pythagoras proved it.

We know much more about the Pythagoreans’ philosophy and beliefs. They understood that mathematics is about abstract concepts, not reality. However, they also believed that these abstractions were somehow embodied in ‘ideal’ concepts, existing in some strange realm of the imagination, so that, for instance, a circle drawn in sand with a stick is a flawed attempt to be an ideal circle, perfectly round and infinitely thin.

The number ten forms a triangle

The most influential aspect of the Pythagorean cult’s philosophy is the belief that the universe is founded on numbers. They expressed this belief in mythological symbolism, and supported it with empirical observations. On the mystic side, they considered the number 1 to be the prime source of everything in the universe. The numbers 2 and 3 symbolized the female and male principles. The number 4 symbolized harmony, and also the four elements (earth, air, fire, water) out of which everything is made. The Pythagoreans believed that the number 10 had deep mystical significance, because 10 = 1 + 2 + 3 + 4, combining prime unity, the female principle, the male principle and the four elements. Moreover, these numbers formed a triangle, and the whole of Greek geometry hinged upon properties of triangles.

The Pythagoreans recognized the existence of nine heavenly bodies, Sun, Moon, Mercury, Venus, Earth, Mars, Jupiter and Saturn, plus the Central Fire, which differed from the Sun. So important was the number 10 in their view of cosmology that they believed there was a tenth body, Counter-Earth, perpetually hidden from us by the Sun.

As we have seen, the whole numbers 1, 2, 3, . . ., naturally lead to a second type of number, fractions, which mathematicians call rational numbers. A rational number is a fraction a/b where a, b are whole numbers (and b is non-zero, otherwise the fraction makes no sense). Fractions subdivide whole numbers into arbitrarily fine parts, so that in particular the length of a line in a geometric figure can be approximated as closely as we wish by a rational number. It seems natural to imagine that enough subdivision would hit the number exactly; if so, all lengths would be rational.

These two shapes are similar

If this were true, it would make geometry much simpler, because any two lengths would be whole number multiples of a common (perhaps small) length, and so could be obtained by fitting lots of copies of this common length together. This may not sound very important, but it would make the whole theory of lengths, areas and especially similar figures – figures with the same shape but different sizes – much simpler. Everything could be proved using diagrams formed from lots and lots of copies of one basic shape.

Unfortunately, this dream cannot be realized. According to legend, one of the followers of Pythagoras, Hippasus of Metapontum, discovered that this statement was false. Specifically, he proved that the diagonal of a unit square (a square with sides one unit long) is irrational: not an exact fraction. It is said (on dubious grounds, but it’s a good story) that he made the mistake of announcing this fact when the Pythagoreans were crossing the Mediterranean by boat, and his fellow cult-members were so incensed that they threw him overboard and he drowned. More likely he was just expelled from the cult. Whatever his punishment, it seems that the Pythagoreans were not pleased by his discovery.

The modern interpretation of Hippasus’s observation is that is irrational. To the Pythagoreans, this brutal fact was a body-blow to their almost religious belief that the universe was rooted in numbers – by which they meant whole numbers. Fractions – ratios of whole numbers – fitted neatly enough into this world-view, but numbers that were provably not fractions did not. And so, whether drowned or expelled, poor Hippasus became one of the early victims of the irrationality, so to speak, of religious belief.

Taming irrationals

Eventually, the Greeks found a way to handle irrationals. It works because any irrational number can be approximated by a rational number. The better the approximation, the more complicated that rational becomes, and there is always some error. But by making the error smaller and smaller, there is a prospect of approaching the properties of irrationals by exploiting analogous properties of approximating rational numbers. The problem is to set this idea up in a way that is compatible with the Greek approach to geometry and proof. This turns out to be feasible, but complicated.

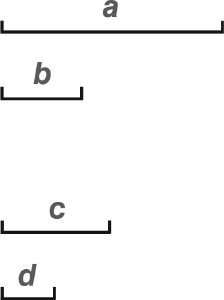
Is the ratio a:b the same as ratio c:d?

The Greek theory of irrationals was invented by Eudoxus around 370 BC. His idea is to represent any magnitude, rational or irrational, as the ratio of two lengths – that is, in terms of a pair of lengths. Thus two-thirds is represented by two lines, one of length two and one of length three (a ratio 2:3). Similarly, is represented by the pair formed by the diagonal of a unit square, and its side (a ratio :1). Note that both pairs of lines can be constructed geometrically.

The key point is to define when two such ratios are equal. When is a:b = c:d? Lacking a suitable number system, the Greeks could not do this by dividing one length by the other and comparing a ÷ b with c ÷ d. Instead, Eudoxus found a cumbersome but precise method of comparison that could be performed within the conventions of Greek geometry. The idea is to try to compare a and c by forming integer multiples ma and nc. This can be done by joining m copies of a end to end, and similarly n copies of b. Use the same two multiples m and n to compare mb and nd. If the ratios a:b and c:d are not equal, says Eudoxus, then we can find m and n to exaggerate the difference, to such an extent that ma > nc but mb < nd. Indeed, we can define equality of ratios that way.

This definition takes some getting used to. It is tailored very carefully to the limited operations permitted in Greek geometry. Nonetheless, it works; it let the Greek geometers take theorems that could easily be proved for rational ratios, and extend them to irrational ratios.

‘The Greek theory of irrationals was invented by Eudoxus around 370 BC.’

Often they used a method called ‘exhaustion’, which let them prove theorems that we would nowadays prove using the idea of a limit and calculus. In this manner they proved that the area of a circle is proportional to the square of its radius. The proof starts from a simpler fact, found in Euclid: the areas of two similar polygons are in the same proportion as the squares of corresponding sides. The circle poses new problems because it is not a polygon. The Greeks therefore considered two sequences of polygons: one inside the circle, the other outside. Both sequences get closer and closer to the circle, and Eudoxus’s definition implies that the ratio of the areas of the approximating polygons is the same as the ratio of the areas of the circles.

Euclid

The best-known Greek geometer, though probably not the most original mathematician, is Euclid of Alexandria. Euclid was a great synthesizer, and his geometry text, the Elements, became an all-time bestseller. Euclid wrote at least ten texts on mathematics, but only five of them survive – all through later copies, and then only in part. We have no original documents from ancient Greece. The five Euclidean survivors are the Elements, the Division of Figures, the Data, the Phaenomena and the Optics.

The Elements is Euclid’s geometrical masterpiece, and it provides a definitive treatment of the geometry of two dimensions (the plane) and three dimensions (space). The Division of Figures and the Data contain various supplements and comments on geometry. The Phaenomena is aimed at astronomers, and deals with spherical geometry, the geometry of figures drawn on the surface of a sphere. The Optics is also geometric, and might best be thought of as an early investigation of the geometry of perspective – how the human eye transforms a three-dimensional scene into a two-dimensional image.

Perhaps the best way to think of Euclid’s work is as an examination of the logic of spatial relationships. If a shape has certain properties, these may logically imply other properties. For example, if a triangle has all three sides equal – an equilateral triangle – then all three angles must be equal. This type of statement, listing some assumptions and then stating their logical consequences, is called a theorem. This particular theorem relates a property of the sides of a triangle to a property of its angles. A less intuitive and more famous example is Pythagoras’s Theorem.

The Elements breaks up into 13 separate books, which follow each other in logical sequence. They discuss the geometry of the plane, and some aspects of the geometry of space. The climax is the proof that there are precisely five regular solids: the tetrahedron, cube, octahedron, dodecahedron and icosahedron. The basic shapes permitted in plane geometry are straight lines and circles, often in combination – for instance, a triangle is formed from three straight lines. In spatial geometry we also find planes, cylinders and spheres.

To modern mathematicians, what is most interesting about Euclid’s geometry is not its content, but its logical structure. Unlike his predecessors, Euclid does not merely assert that some theorem is true. He provides a proof.

Pythagoras’s Theorem: if the triangle has a right angle, then the largest square, A, has the same area as the other two, B and C, combined

What is a proof? It is a kind of mathematical story, in which each step is a logical consequence of some of the previous steps. Every statement that is asserted has to be justified by referring it back to previous statements and showing that it is a logical consequence of them. Euclid realized that this process cannot go back indefinitely: it has to start somewhere, and those initial statements cannot themselves be proved – or else the process of proof actually starts somewhere different.

To start the ball rolling, Euclid started by listing a number of definitions: clear, precise statements of what certain technical terms, such as line or circle, mean. A typical definition is ‘an obtuse angle is an angle greater than a right angle’. The definitions gave him the terminology that he needed to state his unproved assumptions, which he classified into two types: common notions and postulates. A typical common notion is ‘things which are equal to the same thing are equal to one another’. A typical postulate is ‘all right angles are equal to one another’.

Nowadays we would lump both types together and call them axioms. The axioms of a mathematical system are the underlying assumptions that we make about it. We think of the axioms as the rules of the game, and insist that the game is played according to the rules. We no longer ask whether the rules are true – we no longer think that only one game can be played. Anyone who wants to play that particular game must accept the rules; if they don’t, they are free to play a different game, but it won’t be the one determined by those particular rules.

In Euclid’s day, and for nearly 2000 years afterwards, mathematicians didn’t think that way at all. They generally viewed the axioms as self-evident truths, so obvious that no one could seriously question them. So Euclid did his best to make all of his axioms obvious – and very nearly succeeded. But one axiom, the ‘parallel axiom’, is unusually complicated and unintuitive, and many people tried to deduce it from simpler assumptions. Later, we’ll see the remarkable discoveries that this led to.

From these simple beginnings, the Elements proceeded, step by step, to provide proofs of increasingly sophisticated geometrical theorems. For example, Book I Proposition 5 proves that the angles at the base of an isosceles triangle (one with two equal sides) are equal. This theorem was known to generations of Victorian schoolboys as the pons asinorum or bridge of asses: the diagram looks like a bridge, and it was the first serious stumbling block for students who tried to learn the subject by rote instead of understanding it. Book I Proposition 32 proves that the angles of a triangle add up to 180°. Book I Proposition 47 is Pythagoras’s Theorem.

Euclid deduced each theorem from previous theorems and various axioms. He built a logical tower, which climbed higher and higher towards the sky, with the axioms as its foundations and logical deduction as the mortar that bound the bricks together.

Euclid of Alexandria

325–265 BC

Euclid is famous for his geometry book The Elements, which was a prominent – indeed, the leading – text in mathematical teaching for two millennia.

We know very little about Euclid’s life. He taught at Alexandria. Around 45 BC the Greek philosopher Proclus wrote:

‘Euclid . . . lived in the time of the first Ptolemy, for Archimedes, who followed closely upon the first Ptolemy, makes mention of Euclid . . . Ptolemy once asked [Euclid] if there were a shorter way to study geometry than the Elements, to which he replied that there was no royal road to geometry. He is therefore younger than Plato’s circle, but older than Eratosthenes and Archimedes . . . he was a Platonist, being in sympathy with this philosophy, whence he made the end of the whole Elements the construction of the so-called Platonic figures [regular solids].’

Today we are less satisfied with Euclid’s logic, because it has many gaps. Euclid takes a lot of things for granted; his list of axioms is nowhere near complete. For example, it may seem obvious that if a line passes through a point inside a circle then it must cut the circle somewhere – at least if it is extended far enough. It certainly looks obvious if you draw a picture, but there are examples showing that it does not follow from Euclid’s axioms. Euclid did pretty well, but he assumed that apparently obvious features of diagrams needed neither proof nor an axiomatic basis.

This omission is more serious than it might seem. There are some famous examples of fallacious reasoning arising from subtle errors in pictures. One of them ‘proves’ that every triangle has two equal sides.

The golden mean

Book V of the Elements heads off in a very different, and rather obscure, direction from Books I–IV. It doesn’t look like conventional geometry. In fact, at first sight it mostly reads like gobbledegook. What, for instance, are we to make of Book V Proposition 1? It reads: If certain magnitudes are equimultiples of other magnitudes, then whatever multiple one of the magnitudes is of one of the others, that multiple also will be of all.

The language (which I have simplified a little) doesn’t help, but the proof makes it clear what Euclid intended. The 19th-century English mathematician Augustus De Morgan explained the idea in simple language in his geometry textbook: ‘Ten feet ten inches makes ten times as much as one foot one inch.’

What is Euclid up to here? Is it trivialities dressed up as theorems? Mystical nonsense? Not at all. This material may seem obscure, but it leads up to the most profound part of the Elements: Eudoxus’s techniques for dealing with irrational ratios. Nowadays mathematicians prefer to work with numbers, and because these are more familiar I will often interpret the Greek ideas in that language.

Euclid could not avoid facing up to the difficulties of irrational numbers, because the climax to the Elements – and, many believe, its main objective – was the proof that there exist precisely five regular solids: the tetrahedron, cube (or hexahedron), octahedron, dodecahedron and icosahedron. Euclid proved two things: there are no other regular solids, and these five actually exist – they can be constructed geometrically, and their faces fit together perfectly, with no tiny errors.

Two of the regular solids, the dodecahedron and the icosahedron, involve the regular pentagon: the dodecahedron has pentagonal faces, and the five faces of the icosahedron surrounding any vertex determine a pentagon. Regular pentagons are directly connected with what Euclid called ‘extreme and mean ratio’. On a line AB, construct a point C so that the ratio AB:AC is equal to AC:BC. That is, the whole line bears the same proportion to the larger segment as the larger segment does to the smaller.

‘Is it trivialities dressed up as theorems? Not at all.’

If you draw a pentagon and inscribe a five-pointed star, the edges of the star are related to the edges of the pentagon by this particular ratio.

Nowadays we call this ratio the golden mean. It is equal to , and this number is irrational. Its numerical value is roughly 1.618. The Greeks could prove it was irrational by exploiting the geometry of the pentagon. So Euclid and his predecessors were aware that, for a proper understanding of the dodecahedron and icosahedron, they must come to grips with irrationals.

This, at least, is the conventional view of the Elements. David Fowler argues in his book The Mathematics of Plato’s Academy that there is an alternative view – essentially, the other way round. Perhaps Euclid’s main objective was the theory of irrationals, and the regular solids were just a neat application. The evidence can be interpreted either way, but one feature of the Elements fits this alternative theory more tidily. Much of the material on number theory is not needed for the classification of the regular solids – so why did Euclid include this material? However, the same material is closely related to irrational numbers, which could explain why it was included.

The ratio of the diagonals to the sides is golden

Extreme and mean ratio (now called the golden mean). The ratio of the top line to the middle one is equal to that of the middle one to the bottom one

Archimedes

The greatest of the ancient mathematicians was Archimedes. He made important contributions to geometry, he was at the forefront of applications of mathematics to the natural world, and he was an accomplished engineer. But to mathematicians, Archimedes will always be remembered for his work on circles, spheres and cylinders, which we now associate with the number π (‘pi’), which is roughly 3.14159. Of course the Greeks did not work with π directly: they viewed it geometrically as the ratio of the circumference of a circle to its diameter.

Earlier cultures had realized that the circumference of a circle is always the same multiple of its diameter, and knew that this multiple was roughly 3, maybe a bit bigger. The Babylonians used 3⅛. But Archimedes went much further; his results were accompanied by rigorous proofs, in the spirit of Eudoxus. As far as the Greeks knew, the ratio of circumference of a circle to its diameter might be irrational. We now know that this is indeed the case, but the proof had to wait until 1770, when one was devised by Johann Heinrich Lambert. (The school value of 3 ¹/₇ is convenient, but approximate.) Be that as it may, since Archimedes could not prove π to be rational, he had to assume that it might not be.

Greek geometry worked best with polygons – shapes formed by straight lines. But a circle is curved, so Archimedes sneaked up on it by way of approximating polygons. To estimate π, he compared the circumference of a circle with the perimeters of two series of polygons: one series situated inside the circle, the other surrounding it. The perimeters of polygons inside the circle must be shorter than the circle, whereas those outside the circle must be longer than the circle. To make the calculations easier, Archimedes constructed his polygons by repeatedly bisecting the sides of a regular hexagon (six-sided polygon) getting regular polygons with 12 sides, 24, 48 and so on. He stopped at 96. His calculations proved that 3 ¹⁰/₇₁ < π < 3 ¹/₇; that is, π lies somewhere between 3.1408 and 3.1429 in today’s decimal notation.

Archimedes’s work on the sphere is of special interest, because we know not just his rigorous proof, but how he found it – which was decidedly non-rigorous. The proof is given in his book On the Sphere and Cylinder. He shows that the volume of a sphere is two-thirds that of a circumscribed cylinder, and that the surface areas of those parts of the sphere and the cylinder that lie between any two parallel planes are equal. In modern language, Archimedes proved that the volume of a sphere is ⁴/₃ πr³, where r is the radius, and its surface area is 4πr². These basic facts are still in use today.

The proof is an accomplished use of exhaustion. This method has an important limitation: you have to know what the answer is before you have much chance of proving it. For centuries, scholars had no idea how Archimedes guessed the answer. But in 1906 the Danish scholar Heiberg was studying a 13th-century parchment, with prayers written on it. He noticed faint lines from an earlier inscription, which had been erased to make room for the prayers. He discovered that the original document was a copy of several works by Archimedes, some of them previously unknown. Such a document is called a palimpsest – a piece of parchment which has later writing superimposed on erased earlier writing. (Astonishingly, the same manuscript is now known to contain pieces of lost works by two other ancient authors.) One work by Archimedes, the Method of Mechanical Theorems, explains how to guess the volume of a sphere. The idea is to slice the sphere infinitely thinly, and place the slices at one end of a balance; at the other end, similar slices of a cylinder and a cone – whose volumes Archimedes already knew – are hung. The law of the lever produces the required value for the volume. The parchment sold for two million dollars in 1998 to a private buyer.

Archimedes of Syracuse

287–212 BC

Archimedes was born in Syracuse, Greece, son of the astronomer Phidias. He visited Egypt, where supposedly he invented the Archimedean screw, which until very recently was still widely used to raise Nile water for irrigation. He probably visited Euclid in Alexandria; he definitely corresponded with Alexandrian mathematicians.

His mathematical skills were unsurpassed and wide-ranging. He turned them to practical use, and constructed huge war machines based on his ‘law of the lever’, able to hurl huge rocks at the enemy. His machines were used to good effect in the Roman siege of Alexandria in 212BC. He even used the geometry of optical reflection to focus the Sun’s rays on to an invading Roman fleet, burning the ships.

His surviving books (in later copies only) are On Plane Equilibria, Quadrature of the Parabola, On the Sphere and Cylinder, On Spirals, On Conoids and Spheroids, On Floating Bodies, Measurement of a Circle and The Sandreckoner, together with The Method, found in 1906 by Johan Heiberg.

Archimedean screw

Problems for the Greeks

Greek geometry had limitations, some of which it overcame by introducing new methods and concepts. Euclid in effect restricted the permitted geometrical constructions to those that could be performed using an unmarked straight edge (ruler) and a pair of compasses (henceforth ‘compass’ – the word ‘pair’ is technically needed, for the same reason that we cut paper with a pair of scissors, but let’s not be pedantic.) It is sometimes said that he made this a requirement, but it is implicit in his constructions, not an explicit rule. With extra instruments – idealized in the same way that the curve drawn by a compass is idealized to a perfect circle – new constructions are possible.

A sphere and its circumscribed cylinder

For example, Archimedes knew that you can trisect an angle using a straight edge with two fixed marks on it. The Greeks called such procedures ‘neusis constructions’. We now know (as the Greeks must have suspected) that an exact trisection of the angle with ruler and compass is impossible, so Archimedes’s contribution genuinely extends what is possible. Two other famous problems from the period are duplicating the cube (constructing a cube whose volume is twice that of a given cube) and squaring the circle (constructing a square with the same area as a given circle). These are also known to be impossible using ruler and compass.

The Archimedes palimpsest

A far-reaching extension of the allowed operations in geometry, which bore fruit in Arab work on the cubic equation around 800 and had major applications to mechanics and astronomy, was the introduction of a new class of curves, conic sections. These curves, which are extraordinarily important in the history of mathematics, are obtained by slicing a double-cone with a plane. Today we shorten the name to conics. They come in three main types:

• The ellipse, a closed oval curve obtained when the plane meets only one half of the cone. Circles are special ellipses.

• The hyperbola, a curve with two infinite branches, obtained when the plane meets both halves of the cone.

• The parabola, a transitional curve lying between ellipses and hyperbolas, in the sense that it is parallel to some line passing through the vertex of the cone and lying on the cone. A parabola has only one branch, but extends to infinity.

Conic sections

Conic sections were studied in detail by Apollonius of Perga, who travelled from Perga in Asia Minor to Alexandria to study under Euclid. His masterwork, the Conic Sections of about 230 BC, contains 487 theorems. Euclid and Archimedes had studied some properties of cones, but it would take an entire book to summarize Apollonius’s theorems. One important idea deserves mention here. This is the notion of the foci (plural of focus) of an ellipse (or hyperbola). The foci are two special points associated with these two types of conic. Among their many properties, we single out just one: the distance from one focus of an ellipse, to any point, and back to the other focus is constant (equal to the long diameter of the ellipse). The foci of a hyperbola have a similar property, but now we take the difference of the two lengths.

What geometry did for them

Around 250 BC Eratosthenes of Cyrene used geometry to estimate the size of the Earth. He noticed that at midday on the summer solstice, the Sun was almost exactly overhead at Syene (present-day Aswan), because it shone straight down a vertical well. On the same day of the year, the shadow of a tall column indicated that the Sun’s position at Alexandria was one fiftieth of a full circle (about 7.2°) away from the vertical. The Greeks knew that the Earth is spherical, and Alexandria was almost due north of Syene, so the geometry of a circular section of the sphere implied that the distance from Alexandria to Syene is one fiftieth of the circumference of the Earth.

Eratosthenes knew that camel trains took 50 days to get from Alexandria to Syene, and they travelled a distance of 100 stadia each day. So the distance from Alexandria to Syene is 5000 stadia, making the circumference of the Earth 250,000 stadia. Unfortunately we don’t know for sure how long a stadium was, but one estimate is 157 metres, leading to a circumference of 39,250 km (24,500 miles). The modern figure is 39,840 km (24,900 miles).

How Eratosthenes measured the size of the Earth

‘The Greeks knew how to trisect angles and duplicate the cube using conics. . . they could also square the circle.’

The Greeks knew how to trisect angles and duplicate the cube using conics. With the aid of other special curves, notably the quadratrix, they could also square the circle.

Greek mathematics contributed two crucial ideas to human development. The more obvious was a systematic understanding of geometry. Using geometry as a tool, the Greeks understood the size and shape of our planet, its relation to the Sun and Moon, even the complex motions of the remainder of the solar system. They used geometry to dig long tunnels from both ends, meeting in the middle, which cut construction time in half. They built gigantic and powerful machines, based on simple principles like the law of the lever, for purposes both peaceful and warlike. They exploited geometry in shipbuilding and in architecture, where buildings like the Parthenon prove to us that mathematics and beauty are not so far apart. The Parthenon’s visual elegance derives from a host of clever mathematical tricks, used by the architect to overcome limitations of the human visual system and irregularities in the very ground on which the building rested.

The new Wembley stadium. Built using basic principles discovered in Ancient Greece and developed over succeeding centuries by many cultures

The second Greek contribution was the systematic use of logical deduction to make sure that what was being asserted could also be justified. Logical argument emerged from their philosophy, but it found its most developed and explicit form in the geometry of Euclid and his successors. Without solid logical foundations, later mathematics could not have arisen.

Hypatia of Alexandria

AD 370–415

Hypatia is the first woman mathematician in the historical record. She was the daughter of Theon of Alexandria, himself a mathematician, and it is probable that she learned her mathematics from him. By 400 she had become the head of the Platonist school in Alexandria, lecturing on philosophy and mathematics. Several historical sources state that she was a brilliant teacher.

We do not know whether Hypatia made any original contributions to mathematics, but she helped Theon to write a commentary on Ptolemy’s Almagest, and may also have helped him to prepare a new edition of the Elements, upon which all later editions were based. She wrote commentaries on the Arithmetica of Diophantus and the Conics of Apollonius.

Among Hypatia’s students were several leading figures in the growing religion of Christianity, among them Synesius of Cyrene. Some of his letters to her are recorded, and these praise her abilities. Unfortunately, many early Christians considered Hypatia’s philosophy and science to be rooted in paganism, leading some to resent her influence. In 412 the new patriarch of Alexandria, Cyril, engaged in political rivalry with the Roman prefect Orestes. Hypatia was a good friend of Orestes, and her abilities as a teacher and orator were seen as a threat by the Christians. She became a focus for political unrest, and was dismembered by a mob. One source blames a fundamentalist sect, the Nitrian monks, who supported Cyril. Another blames an Alexandrian mob. A third source claims that she was part of a political rebellion, and her death was unavoidable.

Her death was brutal, hacked to pieces by a mob wielding sharp tiles (some say oyster-shells). Her mangled body was then burned. This punishment may be evidence that Hypatia was condemned for witchcraft – indeed, the first prominent witch to be killed by the early Christians – because the penalty for witchcraft prescribed by Constantius II was for their flesh to be ‘torn off their bones with iron hooks’.

Both influences remain vital today. Modern engineering – computer-based design and manufacture, for example – rests heavily on the geometric principles discovered by the Greeks. Every building is designed so that it doesn’t fall down of its own accord; many are designed to resist earthquakes. Every tower block, every suspension bridge, every football stadium is a tribute to the geometers of ancient Greece.

Rational thinking, logical argument, is equally vital. Our world is too complex, potentially too dangerous, for us to base decisions on what we want to believe, rather than on what is actually the case. The scientific method is deliberately constructed to overcome a deep-seated human wish to assume that what we want to be true – what we claim to ‘know’ – really is true. In science, emphasis is placed on trying to prove that what you deeply believe to be the case is wrong. Ideas that survive stringent attempts to disprove them are more likely to be correct.

‘. . . every football stadium is a tribute to the geometers of ancient Greece.’