11 Firm Foundations

Making calculus make sense

By 1800 mathematicians and physicists had developed calculus into an indispensable tool for the study of the natural world, and the problems that arose from this connection led to a wealth of new concepts and methods – for example, ways to solve differential equations – that made calculus one of the richest and hottest research areas in the whole of mathematics. The beauty and power of calculus had become undeniable. However, Bishop Berkeley’s criticisms of its logical basis remained unanswered, and as people began to tackle more sophisticated topics, the whole edifice started to look decidedly wobbly. The early cavalier use of infinite series, without regard to their meaning, produced nonsense as well as insights. The foundations of Fourier analysis were non-existent, and different mathematicians were claiming proofs of contradictory theorems. Words like ‘infinitesimal’ were bandied about without being defined; logical paradoxes abounded; even the meaning of the word ‘function’ was in dispute. Clearly these unsatisfactory circumstances could not go on indefinitely.

Sorting it all out took a clear head, and a willingness to replace intuition by precision, even if there was a cost in comprehensibility. The main players were Bernard Bolzano, Cauchy, Niels Abel, Peter Dirichlet and, above all, Weierstrass. Thanks to their efforts, by 1900 even the most complicated manipulations of series, limits, derivatives and integrals could be carried out safely, accurately and without paradoxes. A new subject was created: analysis. Calculus became one core aspect of analysis, but more subtle and more basic concepts, such as continuity and limits, took logical precedence, underpinning the ideas of calculus. Infinitesimals were banned, completely.

Fourier

Before Fourier stuck his oar in, mathematicians were fairly happy that they knew what a function was. It was some kind of process, f, which took a number, x, and produced another number, f(x). Which numbers, x, make sense depends on what f is. If f(x) = 1/x, for instance, then x has to be non-zero. If f(x) = , and we are working with real numbers, then x must be positive. But when pressed for a definition, mathematicians tended to be a little vague.

The source of their difficulties, we now realize, was that they were grappling with several different features of the function concept – not just what a rule associating a number x with another number f(x) is, but what properties that rule possesses: continuity, differentiability, capable of being represented by some type of formula and so on.

In particular, they were uncertain how to handle discontinuous functions, such as

f(x) = 0 if x ≤ 0, f(x) = 1 if x > 0

This function suddenly jumps from 0 to 1 as x passes through 0. There was a prevailing feeling that the obvious reason for the jump was the change in the formula: from f(x) = 0 to f(x) = 1. Alongside that was the feeling that this is the only way that jumps can appear; that any single formula automatically avoided such jumps, so that a small change in x always caused a small change in f(x).

Another source of difficulty was complex functions, where – as we have seen – natural functions like the square root are two-valued, and logarithms are infinitely many valued. Clearly the logarithm must be a function – but when there are infinitely many values, what is the rule for getting f(z) from z? There seemed to be infinitely many different rules, all equally valid. In order for these conceptual difficulties to be resolved, mathematicians had to have their noses firmly rubbed in them to experience just how messy the real situation was. And it was Fourier who really got up their noses, with his amazing ideas about writing any function as an infinite series of sines and cosines, developed in his study of heat flow.

‘And it was Fourier who really got up their noses. . .’

Fourier’s physical intuition told him that his method should be very general indeed. Experimentally, you can imagine holding the temperature of a metal bar at 0 degrees along half of its length, but 10 degrees, or 50, or whatever along the rest of its length. Physics did not seem to be bothered by discontinuous functions, whose formulas suddenly changed. Physics did not work with formulas anyway. We use formulas to model physical reality, but that’s just technique, it’s how we like to think. Of course the temperature will fuzz out a little at the junction of these two regions, but mathematical models are always approximations to physical reality. Fourier’s method of trigonometric series, applied to a discontinuous function of this kind, seemed to give perfectly sensible results. Steel bars really did smooth out the temperature distribution the way his heat equation, solved using trigonometric series, specified. In The Analytical Theory of Heat he made his position plain: ‘In general, the function f(x) represents a succession of values or ordinates each of which is arbitrary. We do not suppose these ordinates to be subject to a common law. They succeed each other in any manner whatever’.

Bold words; unfortunately, his evidence in their support did not amount to a mathematical proof. It was, if anything, even more sloppy than the reasoning employed by people like Euler and Bernoulli. Additionally, if Fourier was right, then his series in effect derived a common law for discontinuous functions. The function above, with values 0 and 1, has a periodic relative, the square wave. And the square wave has a single Fourier series, quite a nice one, which works equally well in those regions where the function is 0 and in those regions where the function is 1. So a function that appears to be represented by two different laws can be rewritten in terms of one law.

Slowly the mathematicians of the 19th century started separating the different conceptual issues in this difficult area. One was the meaning of the term, function. Another was the various ways of representing a function – by a formula, a power series, a Fourier series or whatever. A third was what properties the function possessed. A fourth was which representations guaranteed which properties. A single polynomial, for example, defines a continuous function. A single Fourier series, it seemed, might not.

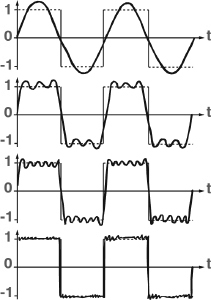
The square wave and some of its Fourier approximations

Fourier analysis rapidly became the test case for ideas about the function concept. Here the problems came into sharpest relief and esoteric technical distinctions turned out to be important. And it was in a paper on Fourier series, in 1837, that Dirichlet introduced the modern definition of a function. In effect, he agreed with Fourier: a variable y is a function of another variable x if for each value of x (in some particular range) there is specified a unique value of y. He explicitly stated that no particular law or formula was required: it is enough for y to be specified by some well-defined sequence of mathematical operations, applied to x. What at the time must have seemed an extreme example is ‘one he made earlier’, in 1829: a function f(x) taking one value when x is rational, and a different value when x is irrational. This function is discontinuous at every point. (Nowadays functions like this are viewed as being rather mild; far worse behaviour is possible.)

For Dirichlet, the square root was not one two-valued function. It was two one-valued functions. For real x, it is natural – but not essential – to take the positive square root as one of them, and the negative square root as the other. For complex numbers, there are no obvious natural choices, although a certain amount can be done to make life easier.

Continuous functions

By now it was dawning on mathematicians that although they often stated definitions of the term ‘function’, they had a habit of assuming extra properties that did not follow from the definition. For example, they assumed that any sensible formula, such as a polynomial, automatically defined a continuous function. But they had never proved this. In fact, they couldn’t prove it, because they hadn’t defined ‘continuous’. The whole area was awash with vague intuitions, most of which were wrong.

The person who made the first serious start on sorting out this mess was a Bohemian priest, philosopher and mathematician. His name was Bernhard Bolzano. He placed most of the basic concepts of calculus on a sound logical footing; the main exception was that he took the existence of real numbers for granted. He insisted that infinitesimals and infinitely large numbers do not exist, and so cannot be used, however evocative they may be. And he gave the first effective definition of a continuous function. Namely, f is continuous if the difference f(x + a) − f(x) can be made as small as we please by choosing a sufficiently small. Previous authors had tended to say things like ‘if a is infinitesimal then f(x + a) − f(x) is infinitesimal’. But for Bolzano, a was just a number, like any others. His point was that whenever you specify how small you want f(x + a) − f(x) to be, you must then specify a suitable value for a. It wasn’t necessary for the same value to work in every instance.

So, for instance, f(x) = 2x is continuous, because 2(x + a) – 2x = 2a. If you want 2a to be smaller than some specific number, say 10⁻¹⁰, then you have to make a smaller than 10⁻¹⁰/2. If you try a more complicated function, like f(x) = x², then the exact details are a bit complicated because the right a depends on x as well as on the chosen size, 10⁻¹⁰, but any competent mathematician can work this out in a few minutes. Using this definition, Bolzano proved – for the first time ever – that a polynomial function is continuous. But for 50 years, no one noticed. Bolzano had published his work in a journal that mathematicians hardly ever read, or had access to. In these days of the Internet it is difficult to realize just how poor communications were even 50 years ago, let alone 180.

‘. . .gradually order emerged from the chaos.’

In 1821 Cauchy said much the same thing, but using slightly confusing terminology. His definition of continuity of a function f was that f(x) and f(x + a) differ by an infinitesimal amount whenever a is infinitesimal, which at first sight looks like the old, poorly-defined approach. But infinitesimal to Cauchy did not refer to a single number that was somehow infinitely small, but to an ever-decreasing sequence of numbers. For instance, the sequence 0.1, 0.01, 0.001, 0.0001 and so on is infinitesimal in Cauchy’s sense, but each of the individual numbers, such as 0.0001, is just a conventional real number – small, perhaps, but not infinitely so. Taking this terminology into account, we see that Cauchy’s concept of continuity amounts to exactly the same thing as Bolzano’s.

Another critic of sloppy thinking about infinite processes was Abel, who complained that people were using infinite series without enquiring whether the sums made any sense. His criticisms struck home, and gradually order emerged from the chaos.

Limits

Bolzano’s ideas set these improvements in motion. He made it possible to define the limit of an infinite sequence of numbers, and from that the series, which is the sum of an infinite sequence. In particular, his formalism implied that

What analysis did for them

The mathematical physics of the 19th century led to the discovery of a number of important differential equations. In the absence of high-speed computers, able to find numerical solutions, the mathematicians of the time invented new special functions to solve these equations. These functions are still in use today. An example is Bessel’s equation, first derived by Daniel Bernoulli and generalized by Bessel. This takes the form

and the standard functions, such as exponentials, sines, cosines and logarithms, do not provide a solution.

However, it is possible to use analysis to find solutions, in the form of power series. The power series determine new functions, Bessel functions. The simplest types of Bessel function are denoted J_k(x); there are several others. The power series permits the calculation of J_k(x) to any desired accuracy.

Bessel functions turn up naturally in many problems about circles and cylinders, such as the vibration of a circular drum, propagation of electromagnetic waves in a cylindrical waveguide, the conduction of heat in a cylindrical metal bar, and the physics of lasers.

Laser beam intensity described by the Bessel function J₁(x)

1 + ¹/₂ + ¹/₄ + ¹/₈ + ¹/₁₆ + . . .

carries on forever, is a meaningful sum, and its value is exactly 2. Not a little bit less; not an infinitesimal amount less; just plain 2.

To see how this goes, suppose we have a sequence of numbers

a₀, a₁, a₂, a₃, . . .

going on forever. We say that a_n tends to limit a as n tends to infinity if, given any number ε > 0 there exists a number N such that the difference between a_n and a is less than whenever n > N (The symbol ε which is the one traditionally used, is the Greek epsilon.) Note that all of the numbers in this definition are finite – there are no infinitesimals or infinities.

To add up the infinite series above, we look at the finite sums

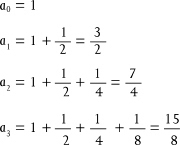
and so on. The difference between a_n and 2 is ¹/₂ⁿ. To make this less than ε we take n > N = log₂ (1/ε).

A series that has a finite limit is said to be convergent. A finite sum is defined to be the limit of the sequence of finite sums, obtained by adding more and more terms. If that limit exists, the series is convergent. Derivatives and integrals are just limits of various kinds. They exist – that is, they make mathematical sense – provided those limits converge. Limits, just as Newton maintained, are about what certain quantities approach as some other number approaches infinity, or zero. The number does not have to reach infinity or zero.

The whole of calculus now rested on sound foundations. The downside was that whenever you used a limiting process, you had to make sure that it converged. The best way to do that was to prove ever more general theorems about what kinds of functions are continuous, or differentiable or integrable, and which sequences or series converge. This is what the analysts proceeded to do, and it is why we no longer worry about the difficulties pointed out by Bishop Berkeley. It is also why we no longer argue about Fourier series: we have a sound idea of when they converge, when they do not and indeed in what sense they converge. There are several variations on the basic theme, and for Fourier series you have to pick the right ones.

Power series

Weierstrass realized that the same ideas work for complex numbers as well as real numbers. Every complex number z = x + iy has an absolute value , which by Pythagoras’s Theorem is the distance from 0 to z in the complex plane. If you measure the size of a complex expression using its absolute value, then the real-number concepts of limits, series and so on, as formulated by Bolzano, can immediately be transferred to complex analysis.

Weierstrass noticed that one particular type of infinite series seemed to be especially useful. It is known as a power series, and it looks like a polynomial of infinite degree:

f(z) = a₀ + a₁z + a₂z² + a₃z³ + . . .

where the coefficients a_n are specific numbers. Weierstrass embarked on a huge programme of research, aiming to found the whole of complex analysis on power series. It worked brilliantly.

For example, you can define the exponential function by

where the numbers 2, 4, 6 and so on are factorials: products of consecutive integers (for instance 120 = 1×2×3×4×5). Euler had already obtained this formula heuristically; now Weierstrass could make rigorous sense of it. Again taking a leaf from Euler’s book, he could then relate the trigonometric functions to the exponential function, by defining

All of the standard properties of these functions followed from their power series expression. You could even define π, and prove that e^iπ = −1, as Euler had maintained. And that in turn meant that complex logarithms did what Euler had claimed. It all made sense. Complex analysis was not just some mystical extension of real analysis: it was a sensible subject in its own right. In fact, it was often simpler to work in the complex domain, and read off the real result at the end.

To Weierstrass, all this was just a beginning – the first phase of a vast programme. But what mattered was getting the foundations right. If you did that, the more sophisticated material would readily follow.

Weierstrass was unusually clear-headed, and he could see his way through complicated combinations of limits and derivatives and integrals without getting confused. He could also spot potential difficulties. One of his most surprising theorems proves that there exists a function f(x) of a real variable x, which is continuous at every point, but differentiable at no point. The graph of f is a single, unbroken curve, but it is such a wiggly curve that it has no well-defined tangent anywhere. His predecessors would not have believed it; his contemporaries wondered what it was for. His successors developed it into one of the most exciting new theories of the 20th century, fractals.

But more of that story later.

A firm basis

The early inventors of calculus had taken a rather cavalier approach to infinite operations. Euler had assumed that power series were just like polynomials, and used this assumption to devastating effect. But in the hands of ordinary mortals, this kind of assumption can easily lead to nonsense. Even Euler stated some pretty stupid things. For instance, he started form the power series

1 + x + x² + x³ + x⁴ + . . .

which sums to 1/(1 − x), set x = −1 and deduced that

1 − 1 + 1 − 1 + 1 − 1 + . . . = ½

which is nonsense. The power series does not converge unless x is strictly between –1 and 1, as Weierstrass’s theory makes clear.

Taking criticisms like those made by Bishop Berkeley seriously did, in the long run, enrich mathematics and place it on a firm footing. The more complicated the theories became, the more important it was to make sure you were standing on firm ground.

‘Even Euler stated some pretty stupid things.’

Today, most users of mathematics once more ignore such subtleties, safe in the knowledge that they have been sorted and that anything that looks sensible probably has a rigorous justification. They have Bolzano, Cauchy and Weierstrass to thank for this confidence. Meanwhile, professional mathematicians continue to develop rigorous concepts about infinite processes. There is even a movement to revive the concept of an infinitesimal, known as non-standard analysis, and it is perfectly rigorous and technically useful on some otherwise intractable problems. It avoids logical contradictions by making infinitesimals a new kind of number, not a conventional real number. In spirit, it is close to the way Cauchy thought. It remains a minority speciality – but watch this space.

Absolute value of the Riemann zeta function

What analysis does for us

Analysis is used in biology to study the growth of populations of organisms. A simple example is the logistic or Verhulst–Pearl model. Here the change in the population, x, as a function of time t is modelled by a differential equation

where the constant M is the carrying capacity, the largest population that the environment can sustain.

Standard methods in analysis produce the explicit solution

which is called the logistic curve. The corresponding pattern of growth begins with rapid (exponential) growth, but when the population reaches half the carrying capacity it begins to level off, and eventually levels off at the carrying capacity.

This curve is not totally realistic, although it fits many real populations quite well. More complicated models of the same kind provide closer fits to real data. Human consumption of natural resources can also follow a pattern similar to the logistic curve, making it possible to estimate future demand, and how long the resources are likely to last.

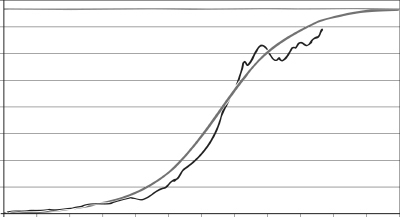
World consumption of crude oil, 1900–2000:smooth curve, logistic equation; jagged curve, actual data