15 Rubber Sheet Geometry

Qualitative beats quantitative

The main ingredients of Euclid’s geometry – lines, angles, circles, squares and so on – are all related to measurement. Line segments have lengths, angles are a definite size with 90° differing in important ways from 91° or 89°, circles are defined in terms of their radii, squares have sides of a given length. The hidden ingredient that makes all of Euclid’s geometry work is length, a metric quantity, one which is unchanged by rigid motions and defines Euclid’s equivalent concept to motion, congruence.

Topology

When mathematicians first stumbled across other types of geometry, these too were metric. In non-Euclidean geometry, lengths and angles are defined; they just have different properties from lengths and angles in the Euclidean plane. The arrival of projective geometry changed this: projective transformations can change lengths, and they can change angles. Euclidean geometry and the two main kinds of non-Euclidean geometry are rigid. Projective geometry is more flexible, but even here subtler invariants exist, and in Klein’s picture what defines a geometry is a group of transformations and the corresponding invariants.

As the 19th century approached its end, mathematicians began to develop an even more flexible kind of geometry; so flexible, in fact, that it is often characterized as rubber-sheet geometry. More properly known as topology, this is the geometry of shapes that can be deformed or distorted in extremely convoluted ways. Lines can bend, shrink or stretch; circles can be squashed so that they turn into triangles or squares. All that matters here is continuity. The transformations allowed in topology are required to be continuous in the sense of analysis; roughly speaking, this means that if two points start sufficiently close together, they end up close together – hence the ‘rubber sheet’ image.

There is still a hint of metric thinking here: ‘close together’ is a metric concept. But by the early 20th century, even this hint had been removed, and topological transformations took on a life of their own. Topology quickly increased in status, until it occupied centre stage in mathematics – even though to begin with it seemed very strange, and virtually content-free. With transformations that flexible, what could be invariant? The answer, it turned out, was quite a lot. But the type of invariant that began to be uncovered was like nothing ever before considered in geometry. Connectivity – how many pieces does this thing have? Holes – is it all one lump, or are there tunnels through it? Knots – how is it tangled up, and can you undo the tangles? To a topologist, a doughnut and a coffee-cup are identical (but a doughnut and a tumbler are not); however, both are different from a round ball. An overhand knot is different from a figure-eight knot, but proving this fact required a whole new kind of machinery, and for a long time no one could prove that any knots existed at all.

It seems remarkable that anything so diffuse and plain weird could have any importance at all. But appearances are deceptive. Continuity is one of the basic aspects of the natural world, and any deep study of continuity leads to topology. Even today we mostly use topology indirectly, as one technique among many. You don’t find anything topological sitting in your kitchen – not obviously, at least. (However, you can occasionally find such items as a chaotic dishwasher, which uses the strange dynamics of two rotating arms to clean dishes more efficiently. And our understanding of the phenomenon of chaos rests on topology.) The main practical consumers of topology are quantum field theorists – a new use of the word ‘practical’ perhaps, but an important area of physics. Another application of topological ideas occurs in molecular biology, where describing and analysing the twists and turns of the DNA molecule requires topological concepts.

Behind the scenes, topology informs the whole of mainstream mathematics, and enables the development of other techniques with more obvious practical uses. It is a rigorous study of qualitative geometric features, as opposed to quantitative ones like lengths. This is why mathematicians consider topology to be of vast importance, whereas the rest of the world has hardly heard of it.

Polyhedra and the Königsberg Bridges

Although topology really only began to take off around 1900, it made an occasional appearance in earlier mathematics. Two items in the prehistory of topology were introduced by Euler: his formula for polyhedra and his solution of the puzzle of the Königsberg Bridges.

In 1639 Descartes had noticed a curious feature of the numerology of regular solids. Consider, for instance, a cube. This has six faces, 12 edges and eight vertices. Add 6 to 8 and you get 14, which is 2 larger than 12. How about a dodecahedron? Now there are 12 faces, 30 edges and 20 vertices. And 2 + 20 = 30, which exceeds 30 by 2. The same goes for the tetrahedron, octahedron and icosahedron. In fact, the same relation seemed tomm work for almost any polyhedron. If a solid has F faces, E edges and V vertices, then F + V = E + 2, which we can rewrite as

F − E + V = 2

Descartes did not publish his discovery, but he wrote it down and his manuscript was read by Leibniz in 1675.

Euler was the first to publish this relationship, in 1750. He followed this up with a proof in 1751. He was interested in the relationship because he had been trying to classify polyhedra. Any general phenomenon such as this one had to be taken into account when performing such a classification.

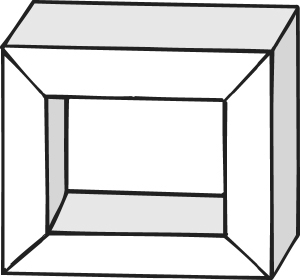
Polyhedron with a hole

Is the formula valid for all polyhedra? Not quite. A polyhedron in the form of a picture frame, with square cross-section and mitred corners, has 16 faces, 32 edges and 16 vertices, so that here F + V − E = 0. The reason for the discrepancy turns out to be the presence of a hole. In fact, if a polyhedron has g holes, then

F + V − E = 2 − 2g

Cauchy’s Proof of the Descartes–Euler Formula

Remove one face and stretch the surface of the solid out on a plane. This reduces F by 1, so we now prove that the resulting plane configuration of faces, lines and points has F − E + V = 1. To achieve this, first convert all faces to triangles by drawing diagonals. Each new diagonal leaves V unchanged, but increases both E and F by 1, so F − E + V remains the same as before. Now start deleting edges, starting from the outside. Each such deletion reduces both F and E, so F − E + V is once more unchanged. When you run out of faces to delete, you are left with a tree of edges and vertices, containing no closed loops. One by one, delete terminal vertices, along with the edge that meets them. Now E and V both decrease by 1, and again F − E + V is unchanged. Eventually this process stops with one solitary vertex. Now F = 0, E = 0 and V = 1, so F − E + V = 1, as required.

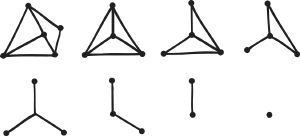
Example of Cauchy’s proof

What, exactly, is a hole? This question is harder than it looks. First, we are talking about the surface of the polyhedron, not its solid interior. In real life we make a hole in something by burrowing through its solid interior, but the above formulas make no reference to the interior of the polyhedron – just to the faces that constitute its surfaces, along with their edges and vertices. Everything we count lies on the surface here. Second, the only holes that change the numerology are those that burrow all the way through the polyhedron – tunnels with two ends, so to speak, not holes like workmen dig in the road. Third, such holes are not in the surface at all, though they are somehow delineated by it. When you buy a doughnut, you also buy its hole, but you can’t buy a hole in its own right. It exists only by virtue of the doughnut, even though in this case you also buy the doughnut’s solid interior.

It is easier to define what ‘no holes’ means. A polyhedron has no holes if it can be continuously deformed, creating curved faces and edges, so that it becomes (the surface of) a sphere. For these surfaces, F + V − E really is always 2. And the converse holds as well: if F + V − E = 2 then the polyhedron can be deformed into a sphere.

The picture-frame polyhedron does not look as though it can be deformed into a sphere – where would the hole go? For a rigorous proof of the impossibility, we need look no further than the fact that for this polyhedron, F + V − E = 0. This relationship is impossible for surfaces deformable to spheres. So the numerology of polyhedra tells us significant features of their geometry, and those features can be topological invariants – unchanged by deformations.

Euler’s formula is now viewed as a significant hint of a useful link between combinatorial aspects of polyhedra, such as numbers of faces, and topological aspects. In fact, it turns out to be easier to work backwards. To find out how many holes a surface has, work out F + V − E − 2, divide by 2, and change sign:

g = − (F + V – E − 2)/2

A curious consequence: we can now define how many holes a polyhedron has, without defining ‘hole’.

An advantage of this procedure is that it is intrinsic to the polyhedron. It does not involve visualizing the polyhedron in a surrounding three-dimensional space, which is how our eyes naturally see the hole. A sufficiently intelligent ant that lived on the surface of the polyhedron could work out that it has one hole, even if all it could see was the surface. This intrinsic point of view is natural in topology. It studies the shapes of things in their own right, not as part of something else.

At first sight, the problem of the Königsberg Bridges bears no relationship to the combinatorics of polyhedra. The city of Königsberg, then in Prussia, was situated on both banks of the river Pregelarme, in which there were two islands. The islands were linked to the banks, and to each other, by seven bridges. Apparently, the citizens of Königsberg had long wondered whether it was possible to take a Sunday stroll that would cross each bridge exactly once.

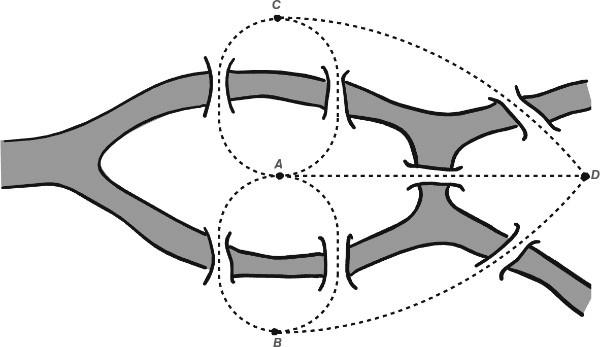
Problem of the Königsberg Bridges C

In 1735 Euler solved the puzzle; rather, he proved that there is no solution, and explained why. He made two significant contributions: he simplified the problem and reduced it to its bare essentials, and then he generalized it, to deal with all puzzles of a similar kind. He pointed out that what matters is not the size and shape of the islands, but how the islands, the banks and the bridges are connected. The whole problem can be reduced to a simple diagram of dots (vertices) joined by lines (edges), here shown superimposed on a map.

To form this diagram, place one vertex on each land-mass – north bank, south bank, and the two islands. Join two vertices by an edge whenever a bridge exists that links the corresponding land masses. Here we end up with four vertices A, B, C, D and seven edges, one for each bridge.

The puzzle is then equivalent to a simpler one about the diagram. Is it possible to find a path – a connected sequence of edges – that includes each edge exactly once?

Euler distinguished two types of path: an open tour, which starts and ends at different vertices, and a closed tour, which starts and ends at the same vertex. He proved that for this particular diagram neither kind of tour exists.

The key to the puzzle is to consider the valency of each vertex, that is, how many edges meet at that vertex. First, think of a closed tour. Here, every edge where the tour enters a vertex is matched by another, the next edge, along which the tour leaves that vertex. If a closed tour is possible, then the number of edges at any given vertex must therefore be even. In short, every vertex must have even valency. But the diagram has three vertices of valency 3 and one of valency 5 – all odd numbers. Therefore no closed tour exists.

A similar criterion applies to open tours, but now there will be exactly two vertices of odd valency: one at the start of the tour, the other at its end. Since the Königsberg diagram has four vertices of odd valency, there is no open tour either.

Euler went one step further: he proved that these necessary conditions for the existence of a tour are also sufficient, provided the diagram is connected (any two vertices are linked by some path). This general fact is a little trickier to prove, and Euler spends some time setting his proof up. Nowadays we can give a proof in a few lines.

Geometric properties of plane surfaces

Euler’s two discoveries seem to belong to entirely different areas of mathematics, but on closer inspection they have elements in common. They are both about the combinatorics of polyhedral diagrams. One counts faces, edges and vertices and the other counts valencies; one is about a universal relation between three numbers, the other a relation that must occur if there exists a tour. But they are visibly similar in spirit. More deeply – and this went unappreciated for more than a century – both are invariant under continuous transformations. The positions of the vertices and edges do not matter: what counts is how they connect to each other. Both problems would look the same if the diagrams were drawn on a rubber sheet and the sheet were distorted. The only way to create significant differences would be to cut or tear the sheet, or glue bits together – but these operations destroy continuity.

The glimmerings of a general theory were apparent to Gauss, who from time to time made quite a lot of fuss about the need for some theory of the basic geometric properties of diagrams. He also developed a new topological invariant, which we now call the linking number, in work on magnetism. This number determines how one closed curve winds round another. Gauss gave a formula to calculate the linking number from analytic expressions for the curves. A similar invariant, the winding number of a closed curve relative to a point, was implicit in one of his proofs of the Fundamental Theorem of Algebra.

Gauss’s main influence on the development of topology came from one of his students, Johann Listing, and his assistant Augustus Möbius. Listing studied under Gauss in 1834, and his work Vorstudien zur Topologie introduced the word topology. Listing himself would have preferred to call the subject geometry of position, but this phrase had been pre-empted by Karl von Staudt to mean projective geometry, so Listing found another word. Among other things, Listing looked for generalizations of Euler’s formula for polyhedra.

It was Möbius who made the role of continuous transformations explicit. Möbius was not the most productive of mathematicians, but he tended to think everything through very carefully and very thoroughly. In particular, he noticed that surfaces do not always have two distinct sides, giving the celebrated Möbius band as an example. This surface was discovered independently by Möbius and Listing in 1858. Listing published it in Der Census Räumlicher Complexe, and Möbius put it in a paper on surfaces.

For a long time Euler’s ideas on polyhedra were something of a side-issue in mathematics, but several prominent mathematicians began to glimpse a new approach to geometry, which they called ‘analysis situs’ – the analysis of position. What they had in mind was a qualitative theory of shape, in its own right, to supplement the more traditional quantitative theory of lengths, angles, areas and volumes. This view began to gain ground when issues of that kind emerged from traditional investigations in mainstream mathematics. A key step was the discovery of connections between complex analysis and the geometry of surfaces, and the innovator was Riemann.

The Riemann sphere

The obvious way to think of a complex function f is to interpret it as a mapping from one complex plane to another. The basic formula w = f(x) for such a function tells us to take any complex number z, apply f to it and deduce another complex number w associated with z. Geometrically, z belongs to the complex plane, and w belongs to what is in effect a second, independent copy of the complex plane.

However, this point of view turns out not to be the most useful one, and the reason is singularities. Complex functions often have interesting points at which their normal, comfortable behaviour goes horribly wrong. For example, the function f(z) = 1/z is well behaved for all z except zero. When z = 0, the value of the function is ¹/₀, which makes no sense as an ordinary complex number, but can with some stretch of the imagination be thought of as infinity (symbol ∞). Specifically, if z gets very close to 0, then 1/z gets very big. Infinity in this sense is not a number, but a term that describes a numerical process: become as large as you wish. Gauss had already noticed that infinities of this type create new types of behaviour in complex integration. They mattered.

Riemann found it useful to include ∞ among the complex numbers, and he found a beautiful geometric way to do this. Place a unit sphere so that it sits on top of the complex plane. Now associate points in the plane with points on the sphere by stereographic projection. That is, join the point in the plane to the North Pole of the sphere, and see where that line meets the sphere.

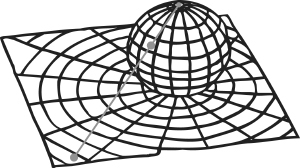
The Riemann sphere and the complex plane

This construction is called the Riemann sphere. The new point at infinity is the North Pole of the sphere – the only point that does not correspond to a point in the complex plane. Amazingly, this construction fits beautifully into the standard calculations in complex analysis, and now equations like ¹/₀ = ∞ make perfect sense. Points at which a complex function f takes the value ∞ are called poles, and it turns out that you can learn a great deal about f if you know where its poles lie.

The Riemann sphere alone would not have drawn attention to topological issues in complex analysis, but a second kind of singularity, called a branch point, made topology essential. The simplest example is the complex square root function, f(z) = . Most complex numbers have two distinct square roots, just like real numbers. These square roots differ only in their sign: one is minus the other. For example, the square roots of 2i turn out to be 1 + i and −1−i, much as the real square roots of 4 are 2 and –2. However, there is one complex number with only one square root, namely 0. Why? Because +0 and –0 are equal.

To see why 0 is a branch point of the square root function imagine starting at the point 1 in the complex plane, and choosing one of the two square roots. The obvious choice is also 1. Now gradually move the point round the unit circle, and as you go, choose, for each position of the point, whichever of the two square roots keeps everything varying continuously. By the time you get half way round the circle, to –1, the square root has only gone a quarter of the way round, to +i, since = +i or −i. Continuing all the way round, we get back to the starting point 1. But the square root, moving at half the speed, ends up at –1. To return the square root to its initial value, the point has to go round the circle twice.

Riemann found a way to tame this kind of singularity, by doubling up the Riemann sphere into two layers. These layers are separate except at the points 0 and ∞, which is a second branch point. At these two points the layers merge – or, thinking about this the other way round, they branch from the single layers at 0 and –∞. Near these special points, the geometry of the layers is like a spiral staircase – with the unusual feature that if you climb two full turns up the staircase, you get back to where you started. The geometry of this surface tells us a lot about the square root function, and the same idea can be extended to other complex functions.

Sphere

Torus

Two-holed torus

The description of the surface is rather indirect, and we can ask what shape is it? It is here that topology comes into play. We can continuously deform the spiral staircase description into something easier to visualize. The complex analysts found that, topologically, every Riemann surface is either a sphere, or a torus, or a torus with two holes, or a torus with three holes, etc. The number of holes, g, is known as the genus of the surface, and it is the same g that occurs in the generalization of Euler’s formula to surfaces.

Orientable surfaces

The genus turned out to be important for various deep issues in complex analysis, which in turn attracted attention to the topology of surfaces. It then turned out that there is a second class of surfaces, which differ from g-holed tori, but are closely related. The difference is that g-holed tori are orientable surfaces, which intuitively means that they have two distinct sides. They inherit this property from the complex plane, which has a top side and a bottom side because the spiral staircases are joined up in a way that preserves this distinction. If instead you joined two flights of the staircase by twisting one floor upside down, the apparently separate sides would join together.

The possibility of this type of joining was first emphasized by Möbius, whose Möbius band has one side and one edge. Klein went one step further, by conceptually gluing a circular disc along the edge of the Möbius band to eliminate the edge altogether. The resulting surface, jokingly named the Klein bottle, has a single side and no edges at all. If we try to draw it sitting inside normal three-dimensional space, it has to pass through itself. But as an abstract surface in its own right (or as a surface sitting inside four-dimensional space) this self-intersection does not occur.

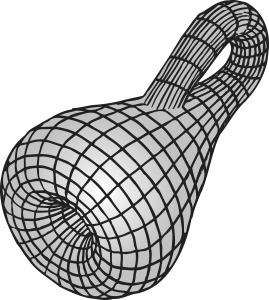
The Klein bottle. The apparent self-intersection is an artefact of its representation in three-dimensional space

The theorem about g-holed tori can be restated like this: any orientable surface (of finite extent with no edges) is topologically equivalent to a sphere with g extra handles (where g might be zero). There is a similar classification of the non-orientable (one-sided) surfaces: they can be formed from a surface called the projective plane by adding g handles.

The combination of these two results is called the Classification Theorem for Surfaces. It tells us, up to topological equivalence, all possible surfaces (of finite extent with no edges). With the proof of this theorem, the topology of two-dimensional spaces – surfaces – could be considered known. That did not mean that every possible question about surfaces could be solved without further effort, but it did give a reasonable place to start from when considering more complicated issues. The Classification Theorem for Surfaces is a very powerful tool in two-dimensional topology.

Jules Henri Poincaré

1854–1912

Henri Poincaré was born in Nancy, France. His father Léon was Professor of Medicine at the University of Nancy, and his mother was Eugénie (née Launois). His cousin, Raymond Poincaré, became the French prime minister and was president of the French Republic during the First World War. Henri came top in every subject at school and was absolutely formidable in mathematics. He had an excellent memory and could visualize complicated shapes in three dimensions, which helped compensate for eyesight so poor that he could hardly see the blackboard, let alone what was written on it.

His first university job was in Caen in 1879, but by 1881 he had secured a far more prestigious job at the University of Paris. There he became one of the leading mathematicians of his age. He worked systematically – four hours per day in two two-hour periods, morning and late afternoon. But his thought processes were less organized, and he often started writing a research paper before he knew how it would end or where it would lead. He was highly intuitive, and his best ideas often arrived when he was thinking about something else.

He ranged over most of the mathematics of his day, including complex function theory, differential equations, non-Euclidean geometry and topology – which he virtually founded. He also worked on applications: electricity, elasticity, optics, thermodynamics, relativity, quantum theory, celestial mechanics and cosmology.

He won a major prize in a competition started in 1887 by King Oscar II of Sweden and Norway. The topic was the ‘three-body problem’ – the motion of three gravitating bodies. The work he actually submitted contained a major mistake, which he quickly corrected; as a result he discovered the possibility of what is now called chaos – irregular, unpredictable motion in a system governed by deterministic laws. He also wrote several bestselling popular science books: Science and Hypothesis (1901), The Value of Science (1905) and Science and Method (1908).

When thinking about topology, it is often useful to suppose that the space concerned is everything that exists. There is no need to embed it in a surrounding space. So doing focuses attention on the intrinsic properties of the space. A vivid image is that of a tiny creature living on, say, a topological surface. How could such a creature, ignorant of any surrounding space, work out which surface it inhabits? How can we characterize such surfaces intrinsically?

By 1900 it was understood that one way to answer such questions is to consider closed loops in the surface, and how these loops can be deformed. For example, on a sphere any closed loop can be continuously deformed to a point – shrunk. For example, the circle running round the equator can be gradually moved towards the north pole, becoming smaller and smaller until it coincides with the north pole itself.

In contrast, every surface that is not equivalent to a sphere contains loops that cannot be deformed to points. Such loops pass through a hole, and the hole prevents them being shrunk. So the sphere can be characterized as the only surface in which any closed loop can be shrunk to a point.

Topology in three dimensions

The natural next step after surfaces – two-dimensional topological spaces – is three dimensions. Now the objects of study are manifolds in Riemann’s sense, except that notions of distance are ignored. In 1904 Henri Poincaré, one of the all-time greats in mathematics, was trying to understand three-dimensional manifolds. He introduced a number of techniques for achieving this goal. One of them, homology, studies the relations between regions in the manifold and their boundaries. Another, homotopy, looks at what happens to closed loops in the manifold as the loops are deformed.

Homotopy is closely related to the methods that had served so well for surfaces, and Poincaré looked for analogous results in three dimensions. Here he was led to one of the most famous questions in the whole of mathematics.

He knew the characterization of the sphere as the only surface in which any closed loop can be shrunk. Did a similar characterization work in three dimensions? For a time he assumed that it did; in fact, this seemed so obvious that he didn’t even notice he was making an assumption. Later he realized that one plausible version of this statement is actually wrong, while another closely related formulation seemed difficult to prove but might well be true. He posed a question, later reinterpreted as the Poincaré conjecture – if a three-dimensional manifold (without boundary, of finite extent, and so on) has the property that any loop in it can be shrunk to a point, then that manifold must be topologically equivalent to the 3-sphere (a natural three-dimensional analogue of a sphere).

Subsequent attempts to prove the conjecture succeeded for generalizations to four or more dimensions. Topologists continued to struggle with the original Poincaré conjecture, in three dimensions, without success.

In the 1980s William Thurston came up with an idea that might make it possible to sneak up on the Poincaré conjecture by being more ambitious. His geometrization conjecture goes further, and applies to all three-dimensional manifolds, not just those in which every loop can be shrunk. Its starting-point is an interpretation of the classification of surfaces in terms of non-Euclidean geometry.

‘The sphere has constant positive curvature.’

The torus can be obtained by taking a square in the Euclidean plane, and identifying opposite edges. As such, it is flat – has zero curvature. The sphere has constant positive curvature. A torus with two or more holes can be represented as a surface of constant negative curvature. So the topology of surfaces can be reinterpreted in terms of three types of geometry, one Euclidean and two non-Euclidean, namely, Euclidean geometry itself, elliptic geometry (positive curvature) and hyperbolic geometry (negative curvature).

What topology did for them

One of the simplest topological invariants was invented by Gauss. In a study of electrical and magnetic fields, he became interested in how two closed loops can link together. He invented the linking number, which measures how many times one loop winds round the other one. If the linking number is non-zero, then the loops cannot be separated by a topological transformation. However, this invariant does not completely solve the problem of determining when two linked loops cannot be separated, because sometimes the linking invariant is zero but the links cannot be separated.

He even developed an analytic formula for this number, by integrating a suitable quantity along the curve concerned. Gauss’s discoveries provided a foretaste of what is now a huge area of mathematics, algebraic topology.

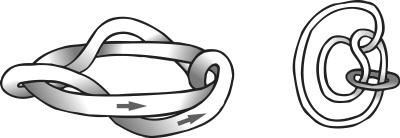
(Left) Loops with linking number 3; (right) these links cannot be separated topologically, even though they have linking number 0

Might something similar hold in three dimensions? Thurston pointed out some complications: there are eight types of geometry to consider, not three. And it is no longer possible to use a single geometry for a given manifold: instead, the manifold must be cut into several pieces, using one geometry for each. He formulated his geometrization conjecture: there is always a systematic way to cut up a three-dimensional manifold into pieces, each corresponding to one of the eight geometries.

The Poincaré conjecture would be an immediate consequence, because the condition that all loops shrink rules out seven geometries, leaving just the geometry of constant positive curvature – that of the 3-sphere.

An alternative approach emerged from Riemannian geometry. In 1982 Richard Hamilton introduced a new technique into the area, based on the mathematical ideas used by Albert Einstein in general relativity. According to Einstein, space-time can be considered as curved, and the curvature describes the force of gravity. Curvature is measured by the so-called curvature tensor, and this has a simpler relative known as the Ricci tensor after its inventor Gregorio Ricci-Curbastro. Changes in the geometry of the universe over time are governed by the Einstein equations, which say that the stress tensor is proportional to the curvature. In effect, the gravitational bending of the universe tries to smooth itself out as time passes, and the Einstein equations quantify that idea.

The same game can be played using the Ricci version of curvature, and it leads to the same kind of behaviour: a surface that obeys the equations for the Ricci flow will naturally tend to simplify its own geometry by redistributing its curvature more equitably. Hamilton showed that the two-dimensional Poincaré conjecture can be proved using the Ricci flow – basically, a surface in which all loops shrink simplifies itself so much as it follows the Ricci flow that it ends up as a perfect sphere. Hamilton also suggested generalizing this approach to three dimensions, and made some progress along those lines, but hit some difficult obstacles.

Perelman

In 2002 Grigori Perelman caused a sensation by placing several papers on the arXiv, a website for physics and mathematics research that lets researchers provide public access to unrefereed, often ongoing, work. The aim of the website is to avoid long delays that occur while papers are being refereed for official publication. Previously, this role had been played by informal preprints. Ostensibly these papers were about the Ricci flow, but it became clear that if the work was correct, it would imply the geometrization conjecture, hence that of Poincaré.

The basic idea is the one suggested by Hamilton. Start with an arbitrary three-dimensional manifold, equip it with a notion of distance so that the Ricci flow makes sense, and let the manifold follow the flow, simplifying itself. The main complication is that singularities can develop, where the manifold pinches together and ceases to be smooth. At singularities, the proposed method breaks down. The new idea is to cut it apart near such a singularity, cap off the resulting holes and let the flow continue. If the manifold manages to simplify itself completely after only finitely many singularities have arisen, each piece will support just one of the eight geometries, and reversing the cutting operations (surgery) tells us how to glue those pieces back together to reconstruct the manifold.

Grigori Perelman

1966 –

Perelman was born in what was then the Soviet Union in 1966. As a student he was a member of the USSR team competing in the International Mathematical Olympiad, and won a gold medal with a 100% score. He has worked in the USA and at the Steklov Institute in St Petersburg, but currently holds no specific academic position. His increasingly reclusive nature has added an unusual human dimension to the mathematical story. It is perhaps a pity that this story reinforces the stereotype of the eccentric mathematician.

The Poincaré conjecture is famous for another reason: it is one of the eight Millennium Mathematics Problems selected by the Clay Institute, and as such its solution – suitably verified – attracts a million-dollar prize. However, Perelman had his own reasons for not wanting the prize – indeed, any reward save the solution itself – and therefore had no strong reason to expand his often-cryptic papers on the arXiv into something more suitable for publication.

Experts in the area therefore developed their own versions of his ideas, trying to fill in any apparent gaps in the logic, and generally tidy up the work into something acceptable as a genuine proof. Several such attempts were published, and a comprehensive and definitive version of Perelman’s proof has now been accepted by the topological community. In 2006 he was awarded a Fields Medal for his work in this area, which he declined. Not everyone craves worldly success.

Topology and the real world

Topology was invented because mathematics could not function without it, stimulated by a number of basic questions in areas like complex analysis. It tackles the question ‘what shape is this thing?’ in a very simple but deep form. More conventional geometric concepts, such as lengths, can be seen as adding extra detail to the basic information captured by topology.

A few early forerunners of topology exist, but it did not really become a branch of mathematics with its own identity and power until the middle of the 19th century, when mathematicians obtained a fairly complete understanding of the topology of surfaces, two-dimensional shapes. The extension to higher dimensions was given a huge boost in the late 19th and early 20th centuries, notably with the investigations of Henri Poincaré. Further advances occurred in the 1920s; the subject really took off in the 1960s, although, ironically, it pretty much lost contact with applied science.

Confounding those critical of the abstraction of 20th century pure mathematics, the resulting theory is now vital to several areas of mathematical physics. Even its most intractable obstacle, the Poincaré conjecture, has now been overcome. In retrospect, the main difficulties in developing topology were internal ones, best solved by abstract means; connections with the real world had to wait until the techniques were sorted out properly.

What topology does for us

In 1956 James Watson and Francis Crick discovered the secret of life the double-helix structure of the DNA molecule, the backbone on which genetic information is stored and manipulated. Today the topology of knots is being used to understand how the two strands of the helix disentangle as the genetic blueprint controls the development of a living creature.

The DNA helix is like a two-stranded rope, with each strand twisted repeatedly around the other. When a cell divides, the genetic information is transferred to the new cells by splitting the strands apart, copying them and joining the new strands to the old in pairs. Anyone who has tried to separate the strands of a long piece of rope knows how tricky this process is: the strands tangle in lumps as you try to pull them apart. In fact DNA is much worse: the helices themselves are supercoiled as if the rope itself has been wound into a coil. Imagine several kilometres of fine thread stuffed into a tennis-ball and you have some idea of how tangled the DNA in a cell must be.

The genetic biochemistry must ravel and unravel this tangled thread, rapidly, repeatedly and faultlessly; the very chain of life depends upon it. How? Biologists tackle the problem by using enzymes to break the DNA chain into pieces, small enough to investigate in detail. A segment of DNA is a complicated molecular knot, and the same knot can look very different after a few tucks and turns have distorted its appearance.

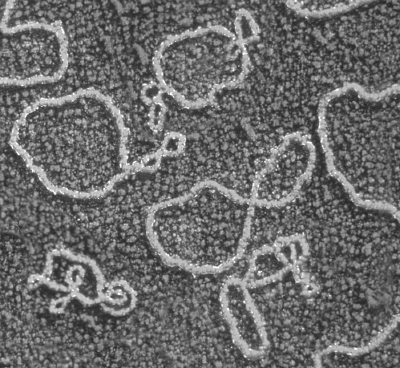
Knotted strands of DNA

The new techniques for studying knots open up new lines of attack on molecular genetics. No longer a plaything of the pure mathematicians, the topology of knots is becoming an important practical issue in biology. A recent discovery is a mathematical connection between the amount of twisting in the DNA helix and the amount of supercoiling.