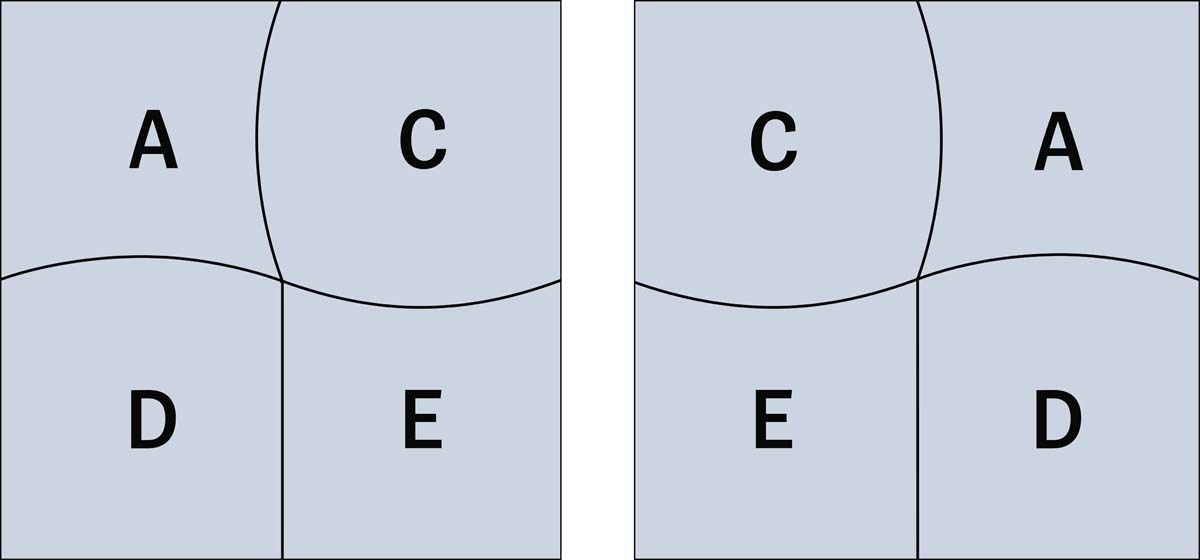
Das Teil B brauchen Sie nicht. Mit A, C, D und E lässt sich leicht ein Quadrat legen. Das kann man durch geschicktes Probieren herausfinden.
Alle Teile haben Wölbungen, manche nach innen, manche nach außen. Es ist offensichtlich, dass bei einem fertig zusammengelegten Puzzle die Anzahl der Wölbungen nach innen exakt der Zahl der Wölbungen nach außen entsprechen muss. Denn Innen- und Außenwölbung passen genau aneinander.
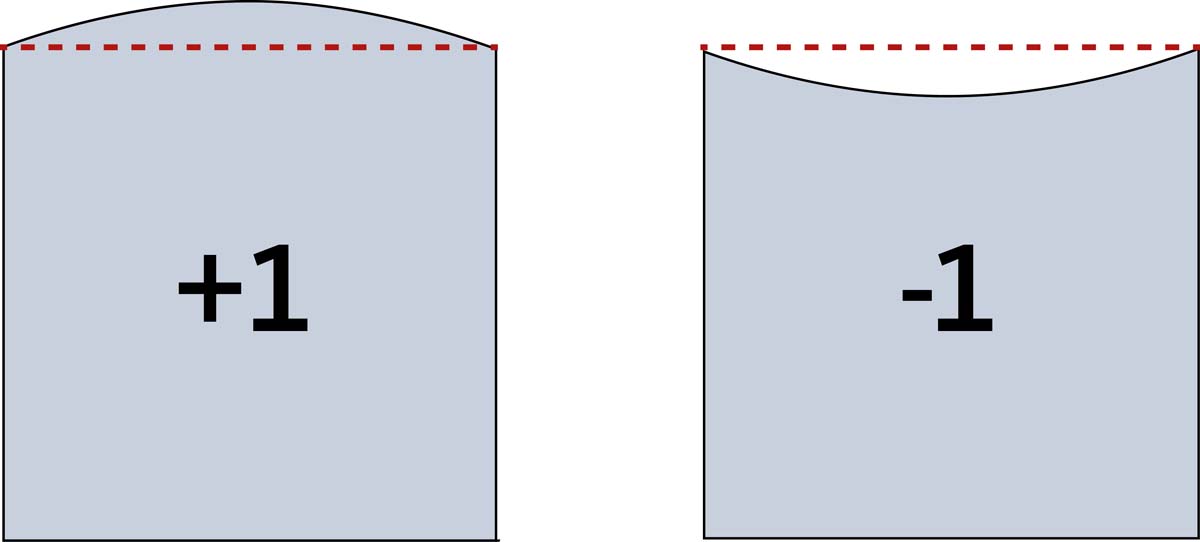
Wir zählen nun bei jedem Puzzleteil die Anzahl der Wölbungen. Diese haben die Form eines Kreissegments. Ist es wie beim linken Puzzleteil (Zeichnung unten) nach außen gewölbt, notieren wir +1. Bei einer Wölbung nach innen wie beim Puzzlestück rechts schreiben wir -1 in das Stück.

Das machen wir so bei allen fünf Puzzlestücken. A hat zwei Einwölbungen – wir notieren -2. Bei B gibt es ein Kreissegment zu viel und eins zu wenig – macht in der Summe 0 – und so weiter und so fort.
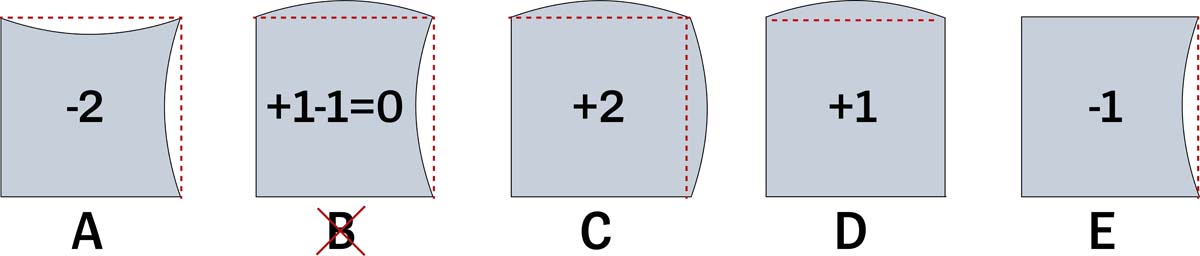
Wenn wir ein Quadrat legen wollen, muss die Summe der Wölbungen aller vier Puzzleteile zusammen null ergeben. Die Summe über alle fünf Segmente ergibt null (-2+0+2+1–1=0).
Damit ist klar, dass B das überflüssige Teil ist. Denn verzichtet man stattdessen auf ein anderes Puzzlestück, ist die Summe der Wölbungen nicht mehr null. Wie viele Lösungen sind möglich?
Weil D und E drei gerade Seiten haben, müssen beide Stücke aneinandergrenzen. Dafür gibt es zwei verschiedene Möglichkeiten (D links und E rechts oder D rechts und E links). A und C können in beiden Fällen nur auf eine Weise angelegt werden – also gibt es exakt zwei verschiedene Lösungen der Aufgabe!