 .
.
Es sind 18,2 Jahre!
Wir berechnen zunächst die Wahrscheinlichkeit dafür, dass die zehn Socken zufällig nach Paaren sortiert sind, wenn wir ein einziges Mal zehn Socken nacheinander aus der Maschine holen.
Nach dem Ziehen der ersten Socke sind noch neun Socken in der Trommel. Aber nur eine davon passt farblich zur bereits gezogenen. Die Wahrscheinlichkeit p1, diese eine Socke zu erwischen, beträgt 1/9.
Mit p1=1/9 hängen nach dem Ziehen von zwei Socken zwei gleichfarbige auf der Leine, acht Socken sind noch in der Maschine. Wir ziehen die dritte Socke und hängen sie auf. Nur eine der verbliebenen sieben Socken hat die gleiche Farbe. Die Wahrscheinlichkeit p2, diese zufällig zu ergreifen, liegt bei 1/7.
Die Wahrscheinlichkeit, dass nach vier herausgenommenen Socken zwei Paare nebeneinander auf der Leine hängen, beträgt deshalb
 .
.
Wir müssen in diesem Fall die einzelnen Wahrscheinlichkeiten miteinander multiplizieren, weil es sich um eine sogenannte bedingte Wahrscheinlichkeit handelt.
Weiter geht es mit der fünften Socke, die wir ziehen und neben die zwei Paare aufhängen. Die Wahrscheinlichkeit p3, dass die sechste Socke zur fünften passt, ist dann 1/5, weil ja nur noch fünf Socken in der Trommel liegen.
Die Wahrscheinlichkeit für drei nebeneinander hängende Sockenpaare beträgt daher
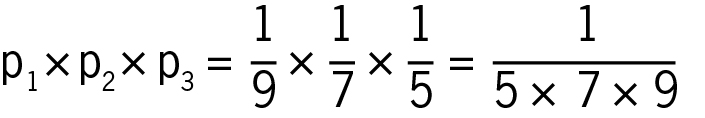 .
.
Auf die gleiche Weise berechnen wir die Wahrscheinlichkeit für vier nebeneinander hängende Sockenpaare:

Diese Zahl entspricht auch der Wahrscheinlichkeit dafür, dass alle zehn Socken nach Paaren sortiert sind, denn wenn dies bereits auf die ersten acht Socken zutrifft, können die letzten beiden in der Trommel verbliebenen Socken nur ein Paar bilden.
Weil die Wahrscheinlichkeit 1/945 beträgt, muss Harald im Durchschnitt 945 Mal seine zehn Socken waschen, damit sie sortiert auf der Leine hängen. Das entspricht 945/52=18,2 Jahren.