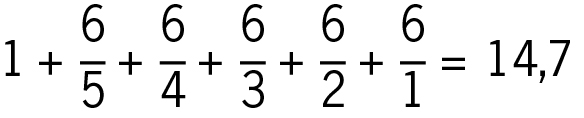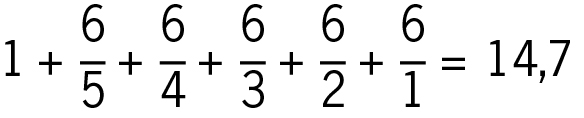
Es sind knapp 15 Würfe. Ist das mehr, als Sie gedacht hatten? Der exakte Wert liegt übrigens bei 14,7.
Die Aufgabe ist verwandt mit dem Sammelbilderproblem. Dabei geht es um die Frage, wie viele Sammelbilder einer Serie mit verschiedenen Motiven man durchschnittlich kaufen muss, bis die Serie vollständig ist.
Das klassische Beispiel dafür sind Sammelalben für große Fußballturniere. Zur EM 2016 gab es 680 verschiedene Motive. Wer auf das Tauschen mit anderen Sammlern verzichtete, musste im Schnitt fast 5000 Sticker kaufen, um jeden Aufkleber dabeizuhaben.
Wir können den Würfel als Serie mit sechs verschiedenen Motiven interpretieren. Jeder Wurf entspricht dem zufälligen Ziehen eines Motivs – und wir möchten jedes Motiv mindestens einmal haben. Mit der Sammelbilder-Formel lässt sich leicht berechnen, wie viele Würfe dafür durchschnittlich nötig sind.
Der erste Wurf ergibt mit einer Wahrscheinlichkeit von 1 eine Augenzahl, die wir noch nicht hatten. Also brauchen wir genau einen Wurf, um eine von sechs Augenzahlen zu haben.
Beim zweiten Wurf ist die Wahrscheinlichkeit p=5/6, eine Zahl zu würfeln, die nicht der zuerst gewürfelten entspricht. Wir brauchen dann im Schnitt 1/p=6/5 Würfe, um zwei verschiedene Augenzahlen zu haben.
Wenn wir zwei verschiedene Augenzahlen haben, beträgt die Wahrscheinlichkeit beim nächsten Wurf p=4/6, eine der vier Zahlen zu würfeln, die noch fehlen. Um eine dieser Zahlen tatsächlich zu würfeln, sind im Mittel 1/p=6/4 Würfe nötig.
So geht es immer weiter: Für die vierte Augenzahl sind im Schnitt 6/3 Würfe erforderlich, für die fünfte 6/2 und für die letzte fehlende Augenzahl schließlich 6/1.
Nun addieren wir diese sechs Zahlen und erhalten so die mittlere Anzahl von Würfen, die man braucht, um alle sechs Augenzahlen mindestens einmal zu haben. Das Ergebnis lautet: