Control Design Considering Mobile Computing

Abstract

In this chapter, an extension of distributed systems considering mobile computing is reviewed. First, A review of some scheduling algorithms is presented to get a good approximation to bounded time delays considering the spend time in all stages of communication and compute. A review of the most important algorithms in terms of consensus and routing is presented. A computer network design is presented from a selection of real-time features, scheduler, task handlers, priorities, precedencies and consensus. Finally, a brief review of control design for mobile conditions is presented with the most representative algorithms in the literature.

5.1 Dynamic Behaviour onto Real Time

Real-time strategies convert the idea of bounded response systems into a dynamic operation, considering the certainty onto time response. To achieve such a goal, the use of scheduling algorithms is preferable. A real-time system is where the interaction amongst elements are with a certainty of time response as global and local through the processing elements. The most common algorithms for real-time are the schedulers, like Earliest Deadline First or Priority Exchange, that manage those tasks in preemptive mode [1].

In particular, one of the most important properties of hard real-time systems is predictability [2]. This means that, based on features of the kernel and the information associated with each task, the system is able to predict the evolution of its tasks and to successively guarantee that all time restrictions are accomplished. However, this is possible only occasionally, due to the high degree of non-determinism of the distributed systems. Several factors introduce scheduling uncertainties, such as the features of the processor and the kernel, the applied scheduling algorithms, the synchronisation mechanisms, the memory management, the communications, the interruption management mechanisms, among others [3].

Distributed systems whose functionality is restricted to accomplishing time deadlines are known as Real-time distributed systems (RTDS), as reviewed in the previous section. These constitute the object study of the present book. Due to the increasing complexity of the interaction of the elements of a RTDS, it is necessary to carry out a more detailed analysis of all real-time aspects that influence the activities of the system.

A real-time application is featured by a set $\varGamma$ of activities, known as tasks, associated with certain time restrictions that have to be accomplished to achieve a wanted behaviour. It is frequent that the n tasks in real-time $\{\tau _{0},\tau _{1},\tau _{2},\ldots , \tau _{n}\}$ execute after some time. From this, a task is understood as a sequence of identical activations $a_{i},i=1,\ldots ,n$ , separated between each other by a time-lapse [3].

The parameters that describe a real-time task are [3, 4]:

1.
Arrival time ( $r_{i}$ ) is the time in which a task is set for execution. It is also referred as release time.
2.
Consumption time ( $c_{i}$ ) is the time that takes to each task to execute its assigned activities without interruption. If it is a hard real-time system, it is considered as the Worst-Case Execution Time (WCET).
3.
Delivery deadline ( $d_{i}$ ) is the limit time in which a task should have finished. If the task is over before or at such an instant, the task is schedulable. If All tasks finish before all their delivery deadlines, the system is schedulable.
4.
Start time ( $s_{i}$ ) is the time in which a task starts its execution.
5.
Finishing time ( $f_{i}$ ) is the time in which a task finishes. It is also known as the response time. A task is schedulable if $f_{i}\le d_{i}$ .
6.
Shifting ( $\varphi _{i}$ ). Occasionally, a task may have a lag or shift since it does not necessarily start exactly at its initial time. Commonly, the start time of the first periodic instance is also known as shift.

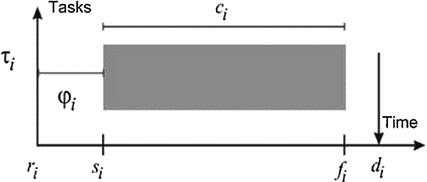
Time parameters of a common task are shown in Fig. 5.1.

../images/321711_1_En_5_Chapter/321711_1_En_5_Fig1_HTML.gif — Fig. 5.1
Time parameters of a common task

Reference [3] considers some further additional time parameters of tasks:

1.
Criticality is a parameter related to the consequences of not accomplishing a deadline.
2.
Value ( $v_{i}$ ) represents the relative importance of a task regarding other tasks. It is not shown in the Fig. 5.1
3.
Delay ( $l_{i}$ ) represents the time delay of a task for achieving its objective regarding its deadline $l_{i}=f_{i}-d_{i}$ .
4.
Laxitude ( $x_{i}$ ) is the maximum time that a task may delay its activation to achieve its deadline.

If all tasks have a shift equal to zero ( $\varphi _{i}=0$ , $\forall i=1,\ldots ,n$ ), this is, all tasks start at the release time, the system is known to be synchronous; otherwise, the system is asynchronous.

There are other classifications for the real-time tasks that depend on the feature taken into consideration [3, 4]:

In terms of the way of execution, tasks may be preemptive or non-preemptive. A preemptive task is that whose execution can be interrupted by other tasks, to be continued later. A non-preemptive task has to be executed until completion of its consumption time, without interruptions.

In terms of the consequences produced by fault, tasks may be critical, if the fault causes catastrophic consequences, or uncritical, if the fault does not cause a serious consequence. Uncritical tasks are commonly used to deal with auxiliary functions, such as system maintenance, non-critical variable monitoring, etc.

In terms of their time characteristics, tasks may be:

1.
Periodical, if their execution should repeat at a constant time interval, known as period ( $p_{i}$ ). A periodical task is a sequence of identical invocations activated at a constant rate. A periodical task is represented as $\tau _{i}$ . Reference [1] describes a periodic task as a sequence of activations with the same parameters. This kind of tasks are characterized by time parameters ( $c_{i},d_{i},p_{i},\varphi _{i}$ ) (Fig. 5.1). The kth activation of a periodic task $\tau _{i}$ is represented as $a_{ik}$ , and it starts at the instant $\varphi _{i}+(k-1)p_{i}$ , and should finish before the instant $\varphi _{i}+(k-1)p_{i}+d_{i}$ .
2.
Aperiodical, if they can be active at non-predictable time instants. For example, aperiodic tasks may be events generated by alarms. Aperiodic tasks can be classified as:
- Without a deadline, which is non-critical, since they have no deadline to accomplish for their finishing. They can arrive at any moment, and they are only defined by their consumption time $c_{i}$ .
- With a hard deadline, they have a non-critical execution deadline. They are characterized by their consumption time and their deadline ( $c_{i},d_{i}$ ).
3.
Sporadical, if a considerable fault is produced when they do not finish before their deadline. They are defined with the same parameters of a periodical task ( $c_{i},d_{i},p_{i}$ ), taking into consideration that the period indicates the minimal time between two consecutive activations.

Scheduling

Basic references about scheduling and scheduling algorithms have been proposed during recent years, regarding their analysis, by [1, 3, 5]. In these, several aspects are used to identify the necessary considerations in the scheduling analysis of the reconfiguration strategies developed later in this book.

A distinctive feature of real-time operating systems is the management of task execution, known as scheduling. For [3], defining the scheduling problem requires to specify three sets: a set of n tasks $\varGamma =\{\tau _{0},\tau _{1},\tau _{2},\ldots ,\tau _{n}\}$ , a set of m processors $\varPi =\{\pi _{1},\pi _{2},\ldots ,\pi _{m}\}$ , and a set of s types of resources $\varPhi =\{\phi _{1},\phi _{2},\ldots ,\phi _{m}\}$ . The precedence between tasks can be specified through an acyclic directed graph, and time restrictions can be associated with each task [3]. In this context, scheduling means to assign processors in $\varPi$ and resources in $\varPhi$ to tasks in $\varGamma$ , aiming to complete all tasks under some imposed restrictions. This problem, in its general form, is NP-complete, and thus, intractable from a computing perspective. Certainly, the complexity of the scheduling algorithms is very relevant in real-time dynamic systems, in which scheduling decisions have to be taken on-line precisely during the execution of tasks.

In particular, when a single processor has to execute a set of concurrent tasks, the processor has to be assigned to different tasks, regarding a predefined criterion, namely the scheduling policy. The set of rules that at any moment determine the order in which tasks execute is known as a scheduling algorithm. The specific operation of the scheduling algorithm of assigning a processor to a particular task is known as dispatch. Hence, a task that could be executed on the processor can be (a) executing, if it has been selected by the scheduling algorithm, or (b) waiting for the processor, if there is another task in execution [1]. Normally, if tasks wait for the processor, they can commonly form a queue for execution. 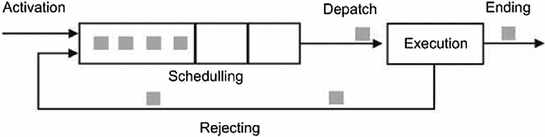Figure 5.2 shows a queue of tasks waiting for execution [3].

../images/321711_1_En_5_Chapter/321711_1_En_5_Fig2_HTML.gif — Fig. 5.2
A queue of tasks waiting for execution

References [3, 6] refer to tasks that potentially can be executed on the processor, independently of its availability, as an active task. A task waiting for the processor is an available task, while a task is currently executed on the processor is a task in execution. All available tasks, waiting for the processor, are kept in a queue known as the available queue. Operating systems that manage several kinds of tasks can have more than an available queue. In many operating systems that allow dynamic activation of tasks, a task in execution can be interrupted at any moment, so a more important task is able to immediately make use of the processor without any waiting in the available queue. In this case, the task in execution is interrupted and placed in the available queue while the processor is assigned to the more important task just at its arrival. The action of suspending a task in execution and place it in the available queue is known as pre-emption. Figure 5.3 shows the states of a process or task [3, 6].

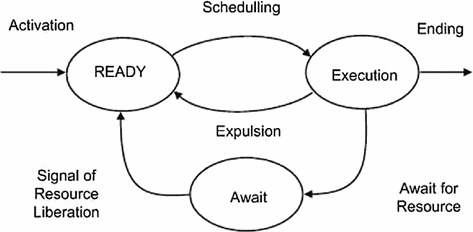
../images/321711_1_En_5_Chapter/321711_1_En_5_Fig3_HTML.gif — Fig. 5.3
States of a process or task

Given a set of tasks $\varGamma =\{\tau _{0},\tau _{1},\ldots ,\tau _{n}\}$ , executing on a single processor, scheduling refers to assigning tasks to the processor, so each task is executed until it finishes. More formally, [3] defines scheduling as a function $\sigma =\mathfrak {R}\rightarrow N$ such that $\forall t\in \mathfrak {R},\exists t_{1},t_{2}$ , and thus, $t\in [t_{1},t_{2})$ and $\forall t\in [t_{1},t_{2}),\sigma (t)=\sigma (t)$ . In other words, $\sigma (t)$ is an integer step function, and $\sigma (t)=k$ , with $$k>0$$ , means that task $\tau _{k}$ is executing at time t, while $\sigma (t)=0$ means that the processor is waiting.

Figure 5.4 shows an example of scheduling when executing a set of tasks $\varGamma =\{\tau _{1},\tau _{2},\tau _{3}\}$ on a processor [3]:

For times $t_{1}$ , $t_{2}$ , $t_{3}$ , and $t_{4}$ , the processor performs a context switch.
Each interval $[t_{i}, t_{i+1})$ in which $\sigma (t)$ is constant, refers to an amount of time in which task $\tau _{i}$ is executing. The interval [x, y) identifies all values of t such that $x\le t<y$ .

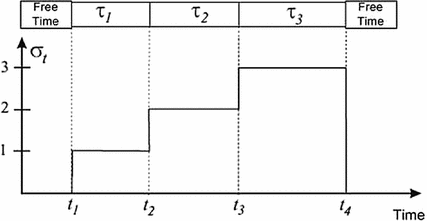
../images/321711_1_En_5_Chapter/321711_1_En_5_Fig4_HTML.gif — Fig. 5.4
An example of scheduling a set of tasks

A preemptive scheduling is that in which executing tasks can be arbitrarily suspended at any moment to assign the processor to another task, regarding a predefined scheduling policy. In this kind of scheduling, tasks can be executed at disjoint time intervals.

A scheduling is called feasible if all tasks can be completed regarding a set of specific restrictions. Thus, a set of tasks is schedulable if there exists at least one algorithm which can produce a feasible scheduling.

A preemptive scheduling of the same example set of tasks $\varGamma$ is shown in Fig. 5.5 [3].

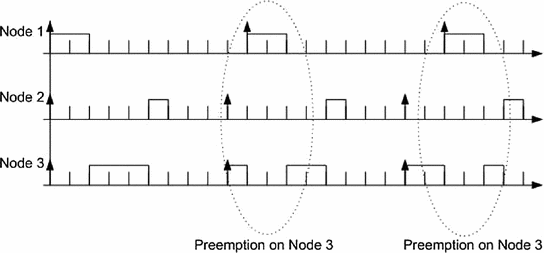
../images/321711_1_En_5_Chapter/321711_1_En_5_Fig5_HTML.gif — Fig. 5.5
A preemptive scheduling of the set of tasks $\varGamma$ between node 3 and node 1

Classification of Scheduling Algorithms

References [1, 3–5] reduce the complexity of implementing a scheduler by simplifying the architecture of the system. They choose a model preemptive or not, using pre-established execution priorities, eliminating precedence and/or limitations of the resources, assuming the activation of simultaneous tasks, sets of homogeneous tasks, this is, exclusively using periodic or aperiodic tasks. All these different features are used to classify several types of scheduling algorithms, proposed by the cited sources.

Among a great variety of scheduling algorithms for real-time tasks, there are the following:

Preemptive. With preemptive algorithms, executing tasks can be interrupted at any moment to assign the processor to another active task, regarding a predefined scheduling policy.
Non-preemptive. With non-preemptive algorithms, a task is executed on the processor until finishing it. In this case, all scheduling decisions are taken when a task finishes its execution.
Static. Static algorithms are those that base their scheduling decisions on fixed parameters, assigned to tasks before their activation.
Dynamic. Dynamic algorithms base their scheduling decisions on dynamic parameters, able to change during the evolution of the system.
Off-line. A scheduling algorithm is used off-line if it is executed over the total set of tasks before their activation. The resulting scheduling is stored in a table and later executed by the dispatcher.
On-line. A scheduling algorithm is said to be used online if the scheduling decisions are taken during the execution time, each time a new task enters the system, or when a task finishes its execution.
Optimal. A scheduling algorithm is named optimal if it minimises some cost function defined over the set of tasks. When there is no such a function, and the only concern is achieving a feasible scheduling, then the algorithm is called feasible (suboptimal) if when using such an algorithm, it always finds the same scheduling.
Heuristic. An algorithm is named heuristic if it tends to find an optimal scheduling, but it does not guarantee it for all cases.

More recent classifications of scheduling algorithms are gathered mainly in [7]:

A static scheduler (off-line) requires the complete information about the scheduling problem at hand (number of tasks, deadlines, priorities, periods, etc.) to be known priori; however, with an online implementation, the configuration changes during execution, and thus, the scheduling problem has to be solved before the scheduler executes it.
A scheduler is dynamic (on-line) if during execution time it is feasible to know the scheduling parameters, as well as performing the proposed configuration changes.

Gambier [7] highlights the advantage of determinism of static schedulers and as a liability their lack of flexibility. On the contrary, dynamic scheduling is very flexible, but it lacks certainty; on-line scheduling may have a poor performance if the system experiments an overload.

Consult [3, 4, 7] for a classification of dynamic schedulers. In this kind of schedulers, there is a family of schedulers called by priorities [3], which for each task, an important value is associated, known as priority. So, always the active task with the highest priority is executed. Priority schedulers can subdivide into the fixed priority schedulers and dynamic schedulers. The fixed priority schedulers, which assign an initial, immutable value of priority to each task, so each task keeps its priority during the whole execution. On the contrary, if the priority of each task changes during execution, then the scheduler is said to be of dynamic priorities.

Within the fixed priorities schedulers, the most common are the Rate Monotonic Scheduler (RMS) [8], which assigns the highest priority to the task with the shortest period, and the Deadline Monotonic Scheduler (DMS), in which the task with the highest priority is that with the closest deadline. Regarding dynamic priorities, the most widely studied algorithms are Earlier Deadline First (EDF) [8], which prioritises according to the absolute deadline, and Least Laxity First (LLF), which assigns the highest priority to the task with the least laxity.

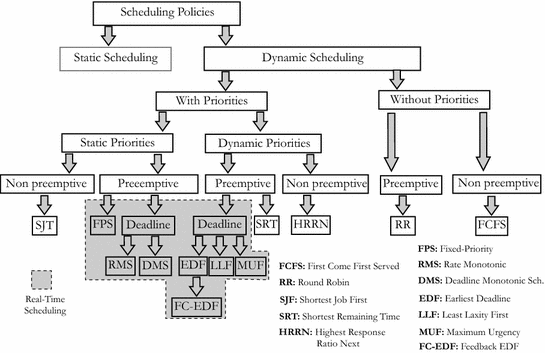
../images/321711_1_En_5_Chapter/321711_1_En_5_Fig6_HTML.gif — Fig. 5.6
Summary of the classification for scheduling algorithms

Figure 5.6 presents a summary of the classification for scheduling algorithms available [7].

Scheduling of Periodic Tasks

In particular, given that in several real-time applications, the activities with the largest demand are constituted by periodic activities, here it is presented a review analysis of schedulability for the most well-known scheduling algorithms of periodic tasks. The schedulability analysis is presented for each algorithm, aiming to derive a guaranteed test for a set of tasks. According to with [1, 3–5], it is important at the beginning to define the used notation and develop the concept of utilisation factor.

The notation to represent the parameters of the task for the schedulability analysis [3] is shown in Table 2.1.

To simplify the schedulability analysis, the following assumptions about the tasks are made [1, 3]:

1.
All instances of a periodic task $\tau _{i}$ are activated with a constant frequency. The interval $p_{i}$ between two consecutive activations is the period of the task.
2.
All the instances of a periodic task $\tau _{i}$ have the same worst execution time $c_{i}$ .
3.
All instances of a periodic task $\tau _{i}$ have the same relative deadline $d_{i}$ , which is equal or less to their period $p_{i}$ .
4.
All tasks in $\varGamma$ are independent, this is, there is no precedence relation or resource restriction among them.

Hence, in the cases of the previous assumptions, a periodic task $\tau _{i}$ can be completely characterized by its shift $\varphi _{i}$ , the period $p_{i}$ (as mentioned before), and the worst execution time $c_{i}$ , and presented as [3]:

$\begin{aligned} \varGamma = \{\tau _i \left( {\varphi _i ,p_i ,c_i } \right) \} \qquad i = 1, \ldots ,n \end{aligned}$

(5.1)

The release time $r_{i,k}$ and the absolute deadline $D_{i,k}$ of the kth instance can be obtained as:

$\begin{aligned} r_{i,k}= & {} \varphi _i + \left( {k - 1} \right) p_i \end{aligned}$

(5.2)

$\begin{aligned} D_{i,k}= & {} r_{i,k} + p_i = \varphi _i + kp_i \end{aligned}$

(5.3)

In such a context, it is considered that a task $\tau _{i}$ is feasible if all its activations finish before their deadlines. A set of tasks $\varGamma$ is schedulable (feasible) if all the tasks within the set are feasible.

Hyperperiod. The concept of hyperperiod is defined as the interval with length $\varLambda$ from which the pattern of activations of the tasks is repeated for a set of periodic tasks $\varGamma$ . It is useful to ensure a scheduling interval as the representation horizon [4]. The maximum number M of activations for n tasks in each hyperperiod is equal to:

$\begin{aligned} M = \sum \limits _{i = 1}^n {\frac{\varLambda }{{p_i }}} \end{aligned}$

(5.4)

The hyperperiod is the minimum common multiple of the periods of all tasks in $\varGamma$ [1].

Utilization Factor. Reference [8] propose a utilization factor of a processor. Given a set $\varGamma$ of n periodic tasks, the utilization factor of the processor is the time fraction that the processor spends in the execution of the set of tasks $\varGamma$ . Given that $c_{i}/p_{i}$ is the time fraction that the processor spends executing a task $\tau _{i}$ , the utilization factor for the n tasks is given as the summation of all the relations of this kind for each task, and bounded as follows:

$\begin{aligned} U = \sum \limits _{i = 1}^n {\frac{{c_i }}{{p_i }}} \le 1 \end{aligned}$

(5.5)

The utilisation factor of the processor provides a measure of the computational load of the processor due to a set of periodic tasks. Although the utilisation of the processor can be improved by incrementing the execution times of the tasks or decreasing their periods, there is a maximum value U under which $\varGamma$ is schedulable, and above which $\varGamma$ is not schedulable. Such a limit depends on the set of tasks, the particular relationships between periods of tasks, and the algorithm used to schedule the tasks.

Let $U_{x}(\varGamma ,A)$ be the superior bound of the utilisation factor of the processor for a set of tasks $\varGamma$ using algorithm A. When $U=U_{x}(\varGamma ,A)$ , it is considered that the set of tasks can be executed by the processor. In such a situation, $\varGamma$ is schedulable by A, but any increment in the execution time of any of the tasks would make the set $\varGamma$ infeasible. For the given algorithm A, the minimal superior bound $U_{mx}(A)$ of the utilisation factor of the processor is the minimum of the utilisation factors of all the sets of tasks that completely make use of the processor:

$\begin{aligned} U_{mx} \left( A \right) = \mathop {\min }\limits _\varGamma U_x \left( {\varGamma ,A} \right) \end{aligned}$

(5.6)

Figure 5.7 shows the meaning of $U_{mx}(A)$ for some scheduling algorithm A. The sets of tasks $\varGamma _{i}$ in the figure differ in the number of tasks and in the value of their periods. When scheduled by algorithm A, each set of tasks $\varGamma _{i}$ totally uses the processor when the utilisation factor $U_{i}$ (changed when modifying the execution times of their tasks) reaches the particular superior bound $U_{x_{i}}$ . If $U_{i}\le U_{x_{i}}$ , then $\varGamma _{i}$ is schedulable; otherwise $\varGamma _{i}$ is not schedulable.

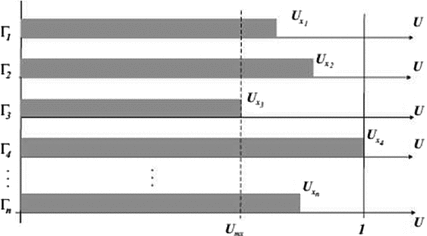
../images/321711_1_En_5_Chapter/321711_1_En_5_Fig7_HTML.gif — Fig. 5.7
$U_{mx}(A)$ for some scheduling algorithm A

Reference [3] points out that each set of tasks is able to have a different maximum bound. Given that $U_{mx}(A)$ is the minimum of all the maximum bounds, any set of tasks that has a utilisation factor of the processor under $U_{mx}(A)$ is schedulable by A.

$U_{x}(A)$ defines an important characteristic of the scheduling algorithms since it allows to easily verify the schedulability if a set of tasks. Certainly, any set of tasks whose utilisation factor is under this bound is schedulable by the algorithm A. In contrast, any utilisation factor above this bound would work if and only if the periods of the tasks are adequately related [1, 3].

If the utilization factor of the processor of a set of tasks is greater than one, the set cannot be schedulable by any algorithm. It is simple to show this, considering standardized periods and consumption times to integer time units. Let P be the product of all periods, $P = p_{1}p_{2}\ldots p_{n}$ ; if $$U > 1$$

, then

, which can be written as:

$\begin{aligned} \sum \limits _{i = 1}^n {\frac{P}{{p_i }}c_i > P} \end{aligned}$

(5.7)

The factor $P/p_{i}$ represents the number of times that $\tau _{i}$ is executed during the interval P, while $Pc_{i}/p_{i}$ is the total computing time required by $\tau _{i}$ in the interval P. Therefore, the sum of the left side of the inequality in Eq. 5.7 represents the total computing time demand required by all tasks in P. Clearly, if such a demand exceeds the available time of the processor, there is no feasible scheduling for the set of tasks [3, 5].

A similar situation is presented in several distributed systems, regardless the communication media, like for example, wireless technology. In this sense, local networks provide an approachable situation like MANET [9].

Related Work. Several technologies have been previously combined to develop a protocol for MANET networks, allowing it to be context-aware. Such a context-aware feature is what allows triggering a distributed task every time an event occurs. In all previous work, the first step to execute a distributed task is to discover which nodes can perform the processes that compose such a distributed task.

This service (or process) discovery, regarding a mobile network, has been an important research topic during the last few years. Examples of these are the SLPManet [10] protocol, which modifies the Service Location Protocol [11] to work in MANET environments. Basically, this protocol establishes that service request packages are broadcasted, while service replies packages are cached by every node. However, due to this protocol is developed at the level of the application layer, it simply cannot access any routeing and scheduling information. Another problem is that cache entries may be false when the network topology changes.

Here, a discovery-less architecture is proposed, similar to [12]. Nevertheless, instead of AODV, DSR [13] is used here. Moreover, the protocols proposed by some related work require that only one service is discovered per message. Here, in order to execute a coordinated task, several processes should be found, and hence, the protocol proposed uses multiple service requests, encapsulated into one DSR route request.

Other approaches have been developed around the study of MANET networks and mobile networks, related to the topic here, such as those presented in [14–16]. These types of study have focused the research on context awareness, instead of process management. Further, the Coordinated Task protocol attempts to keep a low network load by merging all service discovery replies that belong to a particular Coordinated Task. Here, service discovery replies are piggy-backed on DSR route reply packets.

After process discovery, the related Coordinated Task should be executed. However, execute a distributed task on MANET is a challenge because during execution the availability of nodes may change: some mobile nodes become unavailable (they leave the network, or fail). Thus, they have to be replaced by other available nodes.

In [17], a distributed task is modelled as a Task Graph. An on-line algorithm is used to replace the unavailable nodes. However, this does not take into consideration the performance (in terms of execution time) or the network load, which makes this approach not suitable for the problem posed here, as RTDS.

Here, a similar Task Graph approach to [18] is used, but only to represent the data flow among of the processes. However, the network load is considered in order to map processes to nodes. Moreover, local cache information is used for replacing unavailable nodes, instead of performing new service requests.

Coordinated Tasks. A Coordinated Task is specified by using a control-driven coordination model [3, 19]. In this model, every process of the task has two ports: input and output. These ports are the only means of interaction between a process and its environment. Input and output ports from different processes are linked to form a communication flow. This communication model guarantees that the activity of each process is decoupled from the activity of any other process: each process is only in charge of performing a sequence of instructions that consumes and produces data. Data transmission between two nodes is the responsibility of the operating system on those nodes.

Executing a Coordinated Task creates a data flow in the network. This flow, called CT execution flow, is modelled using a Task Graph. The CT execution flow has a root node (represented as p0 in Fig. 5.8). This node contains the process in charge to detect the event that triggers the execution of the Coordinated Task.

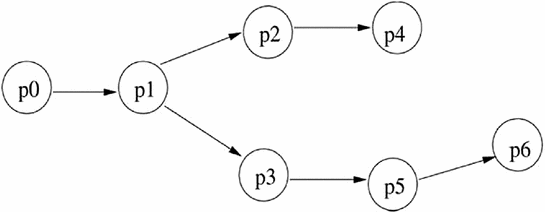
../images/321711_1_En_5_Chapter/321711_1_En_5_Fig8_HTML.gif — Fig. 5.8
Example of a task graph

The CT execution flow is implemented by using an adjacency list. Entries of such a list are tuples, composed of two process ids: one for the source process of the flow, and the other for the destination process. Tuples in the list are ordered according to the flow direction. So, every process may appear as a source or as a destination. For the CT execution flow in Fig. 5.8, the correspondent adjacency list is $$(p_0,p_1),(p_1,p_2),(p_1,p_3),(p_2,p_4),(p_3,p_5),(p_5,p_6)$$ .

Now, the Coordination Task protocol is in charge of mapping processes of the Coordinated Task onto available nodes. This protocol also links the input ports of each process to the corresponding output ports. For the actual purposes, nodes with sensors are specifically used to start a Coordinated Task, and thus, they have a CT execution script per each event. Hence, every Coordinated Task has an associated execution script.

Commonly, the CT execution script includes the following information:

Coordinated Task Name. A unique name that identifies a Coordinated Task.
Trigger Event Identifier. A unique id that represents an event.
Processes Identifiers. A field used to identify a process in a Coordinated Task. Depending on the application, the process id could be represented as simple as integers, or as complex as full XML descriptions, like WSDL.
Processes Adjacency List. The adjacency list, describing the CT execution flow.
Coordinated Task Soft Deadline. Every Coordinated Task should be completed before a deadline, and thus, this field represents such a deadline as a timeout value.
Coordinated Task Maximum Communication Requirement. A list indicating how many data is transmitted by every process for each node. If a node does not produce data, its entry is the size of a CT Message.

Coordinated Task Execution Algorithm. Figure 5.9 shows the algorithm used to execute a Coordinated Task. Step E1 uses a reactive process discovery algorithm, based on encapsulating a discovery message into the DSR routeing protocol [20].

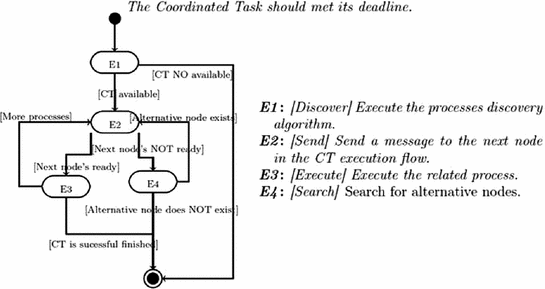
../images/321711_1_En_5_Chapter/321711_1_En_5_Fig9_HTML.gif — Fig. 5.9
Algorithm for executing a coordinated task

Responses to the discovery messages include the process worst execution time and the amount of data produced. These values are used in Eq. 5.8 to obtain the coordinated task execution time $E_{CT}$ .

$\begin{aligned} E_{CT} = T_D + T_T + T_E \end{aligned}$

(5.8)

where $T_{D}$ is the time used by the process discovery procedure, and it is obtained by the node which detects the event. This node is also in charge of starting the process discovery algorithm.

On the other hand, $T_{T}$ is the time needed to transmit the data. To determine $T_{T}$ , it is required to find out the actual network capacity. However, how to do this is still an open issue. Here, an approach similar to that in [9] is followed. So, using the results, the transmission time ( $T_{T}$ ) is calculated by using Eq. 5.9. Notice that, Eq. 5.9 considers that no message is sent in parallel.

$\begin{aligned} T_T = \sum \limits _{i = 1}^k {\left( {\frac{{\sqrt{n} }}{W}L_i } \right) } \end{aligned}$

(5.9)

where k are the processes in the coordinated task, n is the number of nodes available in the network, W is the nominal network bandwidth, in kbytes/second, and $L_{i}$ is the message length in kbytes. This value is obtained from the response to the discovery message.

Finally, $T_{E}$ is the time used by the nodes to execute its assigned processes. It is calculated by simply adding all the worst execution time of each process. These worst execution values are transmitted as a field of the response to the discovery message. Each node obtains these values as presented in [9].

A Coordinated Task is considered feasible if its execution time ( $E_{CT}$ ) satisfies Eq. 5.10, where $D_{CT}$ represents the CT deadline.

$\begin{aligned} E_{CT} \le D_{CT} \end{aligned}$

(5.10)

The following step in the execution flow is started by sending a message to the node (step E2). If there is no MAC ACK message from this node, it is considered that the node is not available, and a search for an alternative node is started (step E4). On the contrary, if the node is available, it executes its processes (step E3). This procedure repeats until the Coordinated Task finishes, or until it is stopped due to the unavailability of any of the nodes required to perform the processes of this particular Coordinated Task. The scenario presented here is the worst case scenario, and therefore, time values are the extreme limits of this bounded process.

Scheduling Analysis

As stated before, commonly, periodic tasks represent the major demand for real-time systems. The need for periodic tasks arises from data acquisition by sensors, control loops, and monitoring systems, among others. Such activities need to be executed cyclically, at specific rates, derived from the requirements of the application. When the application consists of several concurrent tasks with individual time restrictions, the operating system must ensure that each periodic instance is regularly activated at its own rate and be completed before its deadline. For making a schedulable activation, it has to accomplish that the runtime of the task is less or equal to its deadline. In general, if all activations finish before or at the deadline, it is said that the real-time system is schedulable [3].

Feasibility and Optimality. As mentioned before, a valid scheduling is schedulable if each of its tasks is complete before its deadline. It is said that a set of tasks is schedulable regarding a scheduling algorithm if it uses such an algorithm, always producing a feasible scheduling [1]. The most used criterion to measure the performance of a scheduling algorithm is its ability to find a feasible scheduling for a set of tasks, always if such a scheduling exists. A scheduling algorithm is optimal if it always produces a feasible scheduling or what is the same if the set of tasks is feasible to be scheduled. On the contrary, if the optimal algorithm fails to find a feasible scheduling, it can be concluded that the set of tasks cannot be scheduled by another algorithm. Additionally to the criteria based on feasibility, other performance measures include the average value and the maximum finalisation value of a task regarding its deadline (lateness), how much it takes (tardiness), the response time, and the miss rate [1].

Most preemptive scheduling algorithms are priority driven. In this kind of scheduling, each task has associated a priority value, so the active task with the highest priority is always executed. These schedulers are sub-divided into schedulers with fixed priority and schedulers with dynamic priority. Fixed priority schedulers assign an initial priority value to each task, which is kept constant during the whole execution. On the contrary, if the priority of the task changes during execution, then the scheduler is said to be dynamic [4]. To carry out such a kind of scheduling, it is assumed that the time taken by the system to change context is negligible [21].

In particular, four basic algorithms for managing periodic tasks have been developed and extensively used: Rate Monotonic (RM) [8], Deadline Monotonic (DM) [22], Earliest Deadline First (EDF) [8], Least Laxity First (LLF) [2]; the first two make use of fixed priorities, while the other two use dynamic priorities.

In theory, schedulability is developed in two phases: the first phase, analysis, obtains as a result whether the set of tasks is schedulable or not by the selected algorithm; and the second phase, in which the tasks are scheduled. In the case of a dynamic algorithm, scheduling is carried out during execution time [4].

5.2 Consensus and Routing Algorithms

Here several approaches for selecting rates or taking decisions are presented since this definition is basic in order to configure proper mobile distributed systems.

Consensus Algorithms.

The consensus is one of the most widely studied problems in distributed systems. There are several proposals of algorithms for solving the consensus problem, which has been classified into regular, hierarchical, and random. They share some common characteristics, such as they are mainly composed of two operations: proposal and decision, as well as rounds. Each round is composed of both proposal and decision operations. In the proposal operation, a value is postulated to be broadcasted. In the decision operation, a function is applied each round to determine what value is chosen among all those proposals to be the result of that round. The result of the round may be a general consensus, or simply, a previous stage for another round [23].

Considering the notation previously used, a graph $$G = (V;E)$$ represents the network, in which V is the set of all nodes in the network, and E is the set of all edges. Let A be the set of all nodes that participate in the consensus, such that $A \subset V$ . Each node proposes a link from itself to any of its neighbours at one hop. This is described using the notation as $\left. {propose\left( {v,y,c} \right) } \right| v \in A$ , in which y is a neighbor at one hop, and c is the cost associated to that link. For simplicity, this is expressed just as P(c) [23].

Regular Consensus. This is also known as “flooding consensus”. In this kind of consensus algorithm, each node proposes a value, representing which neighbour node y to communicate, in order to reach a certain destiny. The actual node broadcasts this information, so it is evaluated by the other nodes with which it has a connection. If any node disconnects at any moment, its information is still taken into consideration by the other nodes [23].

Hierarchical Consensus. In the hierarchical consensus, all nodes are ordered regarding certain priority. The node with the highest priority imposes its value to all the others, as rounds pass. No node can broadcast its value if its superior has not done so. If the highest priority node disconnects before broadcasting its value, then the value of the following node in the hierarchy is broadcasted. If this node does not fail, then its value is imposed on the rest of the nodes [23].

Random Consensus. This variant of consensus algorithms assures an integrity in the agreement. Each node has an initial value, which the node proposes through the primitive P(c). This algorithm is carried out in rounds, each one composed of two phases. In the first phase, each node proposes a value. If when receiving the proposal of the neighbouring nodes it is detected a predominant value, this value is decided as the result, and it is proposed in the next phase of the round. However, if the node does not find a predominant value, then randomly selects a value among the initial values, and proposes it as the result of the next round.

Average Consensus. This variant of the consensus algorithms ensures convergence in the agreement. Each node proposes an initial value, using the primitive P(c). The algorithm makes use of two rounds, in which (a) an initial value is proposed, and (b) a value is proposed as result, which is the average of the received values.

Routing Algorithms

In a wireless network, nodes may act as routers, allowing the communication of a source node with a destiny node by a series of point-to-point communications or hops from one routing node to the next. Hence, when a communication is requested, it has to be determined if a route exists that may connect the source node with the destiny node. Also, if a route is found, it has to be decided whether to use it or not. If there is no available route, it has to be decided what to do with the communication request.

Each one of these steps represents aspects of the routing problem. The selection of an available route constitutes such a routing problem, requiring that the available routes be defined. Such a definition may be the set of all the allowed routes given the structure of the network, or a convenient subset. This should include a description of the procedure to find routes and to select which route to use if there are more than one available routes. The decision to perform or not a communication through an available route is known as flow control [24].

An important feature of the communication network is that it should allow a route from a source node to a destiny node. If such a route does not change through time, it is called a static route, whereas if it does tend to change, it is called a dynamic route. In general, a routing algorithm is used to determine such a route [25]. There are two well-known routing algorithms for this, proposed by Bellman-Ford and by Dijkstra.

Types of Routing Algorithms. Routing algorithms indicate the route that a message has to take in order to reach its destiny. This is achieved in a wireless network by selecting the adequate output channel, which is selected from a set of possible options. routing algorithms can be classified into three types:

Deterministic.
Completely adaptive.
Partially adaptive.

Routing Table. A routing table is the representation of the available routes within a communication network, from the perspective of a single node. The routing table of a node can be statically constructed, so the resulting routing table does not change through time, or it can be periodically (dynamically) updated, using information of the neighbouring nodes [26].

Adaptive Routing Algorithm. Dynamic routing algorithms allow to adapt to the traffic or topology changes of a network. A dynamic algorithm can be periodically executed, or directly as a response to the changes in the network. Nevertheless, adaptive routing algorithms are prone to route oscillations and loops.

5.3 Computer Network Design

Real-Time Design

A real-time (computing) system is that whose behaviour is fixed by the characteristics of its application [27]. Several characteristics have been identified for analysing and implementing real-time systems. Some of them are listed as follows:

1.
Identify all the tasks that compose an application, as well as their time restrictions, such as deadline, period, activation time, etc., which have to be accomplished.
2.
Specify the way in which to perform interruption management and context change.
3.
Establish the way in which priorities are assigned to tasks.
4.
Specify the way in which tasks are manipulated so they present certain kind of relation.
5.
Perform the correspondent scheduling analysis.
6.
Implement the proposed model.

In general, the design of real-time distributed systems covers the following characteristics [28]:

1.
Clock synchronisation. Synchronisation is a more complex issue in distributed systems than it is in centralised systems since synchronisation in distributed systems requires the use of distributed algorithms. In practice, when there is a computer system or network with n nodes, the corresponding n clocks tend to oscillate at different rates, which implies an asynchronous execution. The difference between the time values is known as clock distortion $\delta$ .
2.
Event-driven systems and time-driven systems. A real-time system is driven by events when the system is able to sense a significative event (using a sensor) and generates an interruption. On the other hand, a real-time system is time-driven when it is handled by a clock interruption each $\varDelta T$ time units. This is known as clock mark. Detecting an event in this kind of real-time systems happens in the clock mark just next to the occurrence of the event. Thus, the selection of a value for $\varDelta T$ should be carefully carried out: if it is too small, the real-time system would have a lot of clock interruptions, wasting time during the revision of the interruptions; if it is too large, crucial events could pass unnoticed.
3.
Predictability. This is an inherent feature of real-time systems. It should be clear that the system accomplishes all its time limits, even during peak loads. The statistical analysis of behaviour, assuming independent events, show the frequent existence of errors, since there are common unexpected correlations between events. Random behaviour seldom occurs in a real-time system.

Desirable Properties of a Real-time System

Timelines. This means that results not only have to be correct but also have to occur within time restrictions.
Design for maximum load.
Predictability.
Fault tolerance.
Maintenance.
Continuous operation.

Basic Concepts

In computing, a process can be defined as the change of the state in the memory due to the action of the processor. As such, a process has an execution thread and can be composed of a finite set of tasks. A task is the sequential execution of code that does not suspend itself. Normally, tasks can be subdivided into smaller units of work, namely, jobs, execution instances, or subtasks. In general, the processor executes tasks in a certain order determined by a set of rules, known as a scheduling algorithm. This algorithm establishes that a task can exist in several states. A task is executing if the task has been chosen for execution or waiting to be assigned to the processor by the scheduling algorithm. A task waiting to be assigned is also known as a ready to execute task. An active task is that has been allocated on a ready to execute queue.

Several operating systems allow the dynamic activation of tasks. An executing task can be temporarily suspended at any moment, and hence, if a more important task requires execution, it can make use of the processor immediately. In this case, the executing task is interrupted and placed on the ready to execute queue, while the processor is assigned to the most important task in the ready to execute queue.

Restrictions

There are basically four types of restrictions to consider:

1.
Restrictions imposed by the operating systems.
2.
Time restrictions.
3.
Precedence restrictions.
4.
Mutual exclusion restrictions, due to shared resources.

Time Restrictions. This kind of restrictions refer to the constraints due to the very application at precise times. A typical time restriction of a real-time task is its deadline, which represents the time in which such a task has to complete its execution without provoking a damage to the system. If a deadline is specified regarding its activation time, then it is known as a relative deadline, while if it is defined regarding the initial time of the system (time zero), it is known as an absolute deadline.

A time restriction is strict if the user requires validation that the system always satisfies its time restrictions. In contrast, a time restriction is flexible if there is no need for such a constant validation, but only that the system statistically satisfies some time restrictions.

In general, a subtask $$J_i$$

executing in real-time can be characterized by a subset of the following parameters (Fig. 5.10):

Activation time . It is the time in which a task is ready for execution; it is also referred as release time.
Consumption time .
Period .
Absolut deadline .
Relative deadline .
Start time
Final time
Response time
Latency :
Laxitud o excedente :
Phase $\phi _i$ :

Precedence Restrictions. Certain computing application require that activities are executed following a specified order, and thus, computing activities cannot be arbitrarily executed, but they have to respect some precedence relations defined during the design stage of the application. Such precedence relations are usually represented as an acyclic directed graph, in which tasks are represented as nodes and precedence relations by edges. The precedence in the graph induces a partial order of execution in the set of tasks.

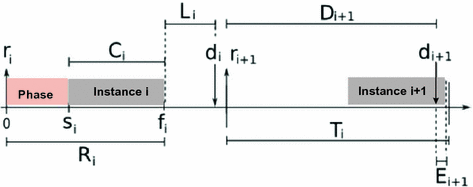
../images/321711_1_En_5_Chapter/321711_1_En_5_Fig10_HTML.gif — Fig. 5.10
Parameters of a subtask executing in real-time

Figure 5.11 shows an acyclic directed graph describing the relations of five tasks ( $J_i \mid i = 1,\ldots ,5$ ). From the graph structure, it can be noticed that task $$J_1$$

is the only task that can start execution since it has no predecessor. Finishing the execution of $$J_1$$

, both

and

are able to start execution. Task $$J_4$$

can start execution only when $$J_2$$

has finished, while $$J_5$$

has to wait until both $$J_2$$

and

finish their respective executions.

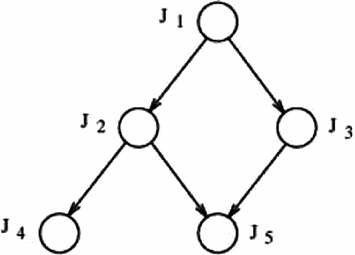
../images/321711_1_En_5_Chapter/321711_1_En_5_Fig11_HTML.gif — Fig. 5.11
An acyclic directed graph describing the relations of five tasks

Mutual Exclusion Restrictions. This kind of restrictions is commonly due to concurrent execution of tasks, which share resources. Consistency problems may arise if two or more tasks make use of shared resources. To secure the consistency, concurrent tasks have to use access protocols, that commonly guarantee mutual exclusion when race conditions arise among concurrent tasks. Hence, these protocols assure a (mutually exclusive) sequential access to the shared resources. In general, most operating systems provide with synchronisation mechanisms that can be used for developing the access protocols.

The Scheduling Problem

In order to define the scheduling problem, it is necessary to define three sets:

1.
A set of n tasks $\varGamma = \{J_1,\ldots ,J_n\}$ ,
2.
a set of m processors $P = \{P_1,\ldots ,P_m\}$ , and
3.
a set of r kinds of resources $R = \{R_1,\ldots ,R_r\}$ .

Besides, there can be some specifications about precedence relations among tasks, as well as time restrictions associated with each task. Thus, scheduling means to assign resources R and processors P to the tasks in $\varGamma$ , aiming to complete all the tasks under the imposed restrictions.

Off-line Scheduling Algorithms

Usually, the feasibility of scheduling is defined in terms of accomplishing time restrictions (deadlines, task dependencies, and so on). For the off-line scheduling algorithms, the solution search space can be represented as a search tree, in which each node represents the assignation of a task to a processor. Any branch to a leaf represents a schedule, although it is not necessarily feasible. A partial scheduling is a route between any pair of nodes in the tree.

Once assignation has been done by each node in the tree, the algorithm traverses the tree by means of a deep search, running all those branches that do not offer a feasible scheduling, i.e., do not accomplish with the specified restrictions. When the search finishes, each possible route represents a possible schedule. In case of which there is more than one feasible schedule, the objective is to find the optimal schedule, in which optimality is defined as a function that has to be maximised or minimised. Examples of these functions are the average load, the maximum workload, reducing execution time, reducing execution latency, etc.

On-line Scheduling Algorithms

Periodic Tasks Scheduling. The existence of periodic tasks in a computing system is due to the need to produce a response, acquire, and process data with certain regularity. Basically, the scheduling strategies distribute processor time so the temporal restrictions are satisfied.

Here, three periodic tasks scheduling techniques are reviewed: rate monotonic (RM), earliest deadline first (EDF), and deadline monotonic (DM). These algorithms are based on priority, which requires that the processor remains idle only when no executing task requires such resources. Algorithms based on priority can be static or dynamic. In a static algorithm, all tasks are divided into subsets. In contrast, in a dynamic algorithm, ready for execution tasks are placed on a queue, and are dispatched to processors for their execution as soon as a processor is made available.

These techniques are widely used in real-time systems, since using these algorithms it is possible to specify a criterion for the use of the available resources in a system. Scheduling algorithms allow the rational utilisation of resources, and occasionally, with the adequate conditions, they can reach optimal solutions. Unfortunately, it is simply not possible to establish rules that define when there are optimal conditions for implementing a specific approach, and totally take advantage of the resources.

Rate Monotonic. The RM algorithm [8] executes under the following assumptions:

1.
Tasks are totally preemptive and, besides, the exchange between tasks has a negligible cost.
2.
Only processing requirements are significative. Memory and I/O are negligible.
3.
All tasks are independent, this is, there is no precedence relationship.
4.
All tasks are periodic.
5.
Relative deadlines of tasks are equal to their periods.

In this scheduling algorithm, priorities are fixed, since they are assigned based on the period: the task with the shortest period is the one with the highest priority. In other words, for a finite set of periodic tasks $\varGamma = {\tau _i : i = 1,\ldots ,N}$ , whose periods $$T_i$$ accomplish that $T_1< T_2< \ldots < T_N$ , the task with the identifier $$i = 1$$ is the one with the highest priority.

To verify if a set of tasks is schedulable using this algorithm, there is a schedulability test, which consists of verifying that the total utilization of tasks is not greater than $N\left( {2^{{1/N}} - 1} \right)$ :

$\begin{aligned} U = \sum \limits _{i = 1}^N {\frac{{C_i }}{{T_i }}} < N\left( {2^{{1/N}} - 1} \right) \le 1 \end{aligned}$

(5.11)

Deadline Monotonic. The DM algorithm [8] executes under the following assumptions:

1.
Tasks are totally preemptive, and the cost of such a property is negligible.
2.
Only processing requirements are significative. Memory, I/O, and other requirements are negligible.
3.
All tasks are independent. There is no precedence relationship.
4.
All tasks are periodic.
5.
Periodic tasks do not have the same relative deadline.

Earliest Deadline First. The EDF algorithm [8] executes under the following assumptions:

1.
All tasks $\tau _i$ have the same worst execution time .
2.
Tasks are totally preemptive, and the cost of this is negligible.
3.
All tasks are independent. There is no precedence relationship.

Scheduling Tasks in Multiple Processors and Distributed Systems

Multiple processor systems require a communication media for the information exchange. Depending on characteristics of the memory architecture, there are two types of multiprocessor systems: shared memory, which implies the existence of a physical memory, shared among the processors of the system, and distributed memory, in which processors do not have a common memory, but communicate using I/O operations.

Shared memory multiprocessor systems are commonly tightly coupled systems, this is, the communication time between processor is very small when compared with the processing time of a task, and thus, can be ignored. Hence, communication is reduced to read and write operations over the shared memory. Distributed memory multiprocessor systems, in contrast, are loosely coupled, since the communication time between processors tends to be comparable to the processing time of tasks.

Real-time scheduling of distributed systems with multiple processors poses two subproblems: assigning tasks to processors, and scheduling of tasks on individual processors. The problem of assigning tasks refers to how to divide the set of tasks, and then, how to assign them to processors. The assigning tasks problem can be static or dynamic.

Static Assingning

Balancing Algorithm. This algorithm consists of a centralised data structure, i.e., a queue, which maintains tasks in incremental order, according to their utilisation. So, tasks are removed one by one from the data structure, each time sending them to the node with the least utility [29].

The objective function to minimize in this algorithm is $\sum \nolimits _{i = 1}^n {\left| {u - u_i } \right| }$ , where u is the average utilization of the processors in the system, and $$u_i$$ is the utilization value of processor i. This algorithm is factible when the number of processors in the system is odd.

Algorithm Next-Fit for Rate Monotonic. In this algorithm [8], a set of tasks is divided, so each subset of tasks is assigned to a processor that makes use of Rate Monotonic for scheduling. This algorithm attempts to use the least number of possible processors. This algorithm, when compared with the balancing algorithm, does not require that the set of processors be given beforehand or predetermined. This algorithm classifies different tasks depending on their utilisation. One or more processors are assigned to a certain kind of task. The essence of this algorithm is grouping tasks with a similar utilisation for their execution.

Tasks are classified regarding their utilization through the following policy: if tasks are to be divided into m classes, a task $\tau _i$ belongs to class k, such that $0 \le k < m$ , if and only if:

$\begin{aligned} \left( {2^{\frac{1}{{k + 1}}} - 1} \right) < \frac{{C_i }}{{T_i }} \le \left( {2^{\frac{1}{k}} - 1} \right) \end{aligned}$

(5.12)

Buddy algorithm. This algorithm aims to overcome the high amount of communications of the auction algorithm [8]. In this algorithm, a processor can be in two states: overload or underload. A processor ( $$P_i$$

) has the status of underloaded if its utilization is not larger than a pre-established value Th, ( $$u_i < Th$$

). A processor is overloaded if this value is over such a pre-established value ( $u_i \ge Th$ ). In this algorithm, a processor sends its information only when its status changes from overloaded to underloaded, or vice versa.

Scheduling of Coordinated Tasks

The Coordination Triggered Protocol (CTP) enables nodes of the system with the capacity to coordinate among themselves, aiming to carry out a coordinated task. Such a coordinated task is composed of several processes, distributed throughout the network. CTP performs the following main functions [19]:

1.
Mapping processes to nodes.
2.
Provide mechanisms that nodes require to perform the coordinated task.
3.
Provide a communication infrastructure.
4.
Monitor the execution status of a coordinated task.
5.
Guarantee that at the end nodes release their used resources.

Consensus

Consensus is a procedure, this is, a finite number of steps whose purpose is reaching an agreement about some value. An important aspect of achieving consensus, applied for many practical situations, is that consensus should be achieved in the presence of faults. Achieving consensus in a distributed system without faults seems not to be a real challenge. It is enough to exchange messages with the needed information to achieve an agreement [30]. In contrast, when a decision is taken even in the presence of faults, or if the consensus interacts with a scheduling algorithm, the problem seems more interesting.

Agreements in the consensus not only allow establishing the value of some important variables in distributed systems. In practice, a consensus is very important to maintain consistency in some systems. Consensus has been studied based on different types of system models: for time models, as synchronous and asynchronous models; for fault models, under byzantine, crash, or due to communication faults. Regarding asynchronous systems, the consensus is restricted by the result produced by Fischer, Lynch, and Patterson (FLP), which assures that it is impossible to reach a deterministic consensus in an asynchronous system [31].

5.4 Control Design Using Local Mobile Conditions

Energy consumption for mobile nodes is an interesting and important issue in order to determine how confident is a node in the network and how stable maybe the system, however, a deep exploration in the issue is out of the scope of this book, interesting references have studied this issue as follows.

Routing Information Protocol (RIP)

Each node builds a unidimensional array (a vector) that contains the distances (costs) to all nodes and distributes such a vector to their immediate neighbours. Initially, it is assumed that each node is aware of the link cost to each one of its immediate neighbours. A fallen link is considered to have an infinite cost [32].

The routing protocols are different from the graph model previously described. In a group of networks, the aim of routers is to learn how to re-send packets to several networks. Thus, instead of considering the cost of reaching other routers, routers broadcast the costs for reaching a particular network.

RIP is the most direct implementation of routing by distance vector. A router that makes use of RIP sends calls every 30 s. It also sends calls when there is a change in its routing table. In practice, the protocol attempts to reach the target in less than 16 hops. In fact, 16 hops are equivalent to an infinite distance [32].

Open Shortest Path First (OSPF)

routing by link state is the second more used routing protocol. The initial considerations are the same as RIP. It is assumed that each node is able to detect the state of the links which communicate with immediate neighbours (connected or disconnected) and the cost of each link [32].

In practice, each router independently obtains its own routing table from the state packet of link 5. This is used to perform Dijkstra’s Search Forward algorithm.

Optimized Link State Routing (OLSR)

OLSR is a proactive routing protocol that distributes jobs to establish connections between nodes in an ad-hoc wireless network. Flooding (direct broadcast of information throughout all the network) is inefficient and very costly for a mobile wireless network, due to bandwidth limitations and scarce channel quality. OLSR provides an efficient mechanism for information broadcast, based on Multipoint Relays (MPR) [33]. Using MPR, instead of allowing each node to re-transmit any received message (as stated in classic flooding), all nodes in the network select among their neighbours a set of multipoint relays. These are in charge of retransmitting the messages sent by the actual node. The other neighbours cannot re-transmit. This reduces the traffic generated by a flooding [33].

Independently of the way for electing them, the set of MPRs of a node should verify that they are able to reach all the neighbours at a distance of two hops from the actual node. This is a covering criterion of the MPR [33].

Topology Control (TC) messages are periodically and asynchronously sent. Through these, nodes inform about the close network topology. In contrast with HELLO, TC messages are global and should reach to all nodes in the network.

Temporally-Ordered Routing Algorithm (TORA)

TORA is a distributed routing protocol for mobile wireless networks. This protocol aims for a high degree of scalability using a flat algorithm, this is a non-hierarchical routing algorithm. This algorithm attempts to suppress the propagation of control messages to the most far away levels of the network. TORA builds up and maintains a directed acyclic graph, with root in its destiny [34].

TORA is a reactive protocol, characterised by providing to the sender node, not only one, but multiple trajectories to arrive at its destination. The procedure is as follows: each node performs a copy of TORA for each destiny, and the protocol creates, maintains, and cancels the routing trajectories. TORA associates a weight to each node of the network, depending on its destiny. Thus, messages move from a node with larger weight to a node with less weight, while routes discovered by QRY (query) packets are updated with those of type UPD (Update) [34].

The node that responds makes use of the UPD packet, adding its weight. UPD packets are broadcasted, so this allows to all nodes in the middle to conveniently update their weights. From this, all nodes aiming to a far or unreachable destiny increase their local weight up until reaching an allowed maximum value, while a node that finds a close neighbour with a weight tending to infinity will change trajectory [34].

The TORA protocol supports the Internet MANET Encapsulation Protocol (IMEP), which provides a trustworthy expedition service for routing protocols. Adding into a unique block IMEP and TORA messages reduce the network overhead and test the state of neighbouring nodes. To obtain such an addition, it is periodically used the exchange of two messages, known as BEACON and HELLO [34].

Related Work

In an ad-hoc network, all nodes send a HELLO message to check their connectivity with their neighbouring nodes. In this scheme, each node keeps an information table about its neighbouring nodes. The agent node broadcasts a request to all neighbouring nodes, and these resend this request to their neighbours, and so on. When all neighbours are covered, a convercast message is sent with the node address, and its adjacency matrix considering all its neighbours. When this message is received, the agent node obtains the adjacency matrix of one hop for each node in all the network. It may be the case that a node receives more than two messages. In this case, the node checks the sequence number of the message, and stores it or updates the adjacency matrix with the larger sequence number [35].

Another important related work in this area refers to the routing algorithms that attempt to avoid or diminish the use of broadcast. This is the case of the Bypass Routing algorithm [36], which behaves as a recovery mechanism for routes and local errors. Essentially, this algorithm recovers from a failed route. First, the node searches for an alternative route in its route cache memory. If the route exists, the node patches the broken route with an alternative route.

In the context of consensus algorithms, one of the most outstanding related work regarding our case study is the voting algorithm using a weight average [37]. This algorithm proposes a novel way to incorporate consensus using the average of the received votes as initial values.

5.5 Concluding Remarks

the mobile computing is studied considering consensus and routing algorithms as the respective strategies for local agreements in order to provide a coherence in particular movements. This sort of strategy and integrated to scheduling approximation lead us to a more complex time delay behaviour that modifies the relationship of local sensor-controller and controller-actuator time delays as presented in the last part of this chapter.

References