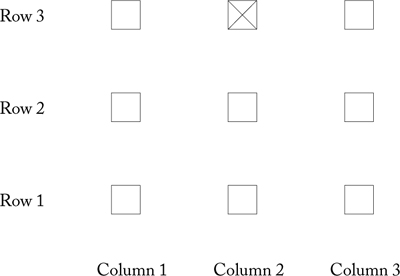
To illustrate the idea of a coordinate system, you can start with the following card trick. Deal out nine cards, face up, in the arrangement shown in the picture.

Tell your student that to perform the trick they must be able to identify the rows and columns of the array: the columns run vertically and the rows run horizontally. In mathematical applications, the columns of an array are often numbered in increasing order from right to left and the rows are numbered in increasing order from bottom to top (as shown in the picture).
Positions in the array are identified by a column number, followed by a row number. For instance, the position marked with an X in the diagram is in column 2, row 3. Give your student a column number and a row number and ask them to identify the card in that position in your array. Repeat this until your student can quickly find any position (you might use larger arrays, too). Then point to a card and ask your student to tell you its column number and row number. Repeat this until your student can name any position. (Make sure your student knows that they should always name the column first, then the row, and that the rows are numbered in increasing order from the bottom up, as in the figure above.)
Tell your student that positions in an array can be represented by dots, and that as a short form the column number and row number can be represented by an ordered pair of numbers in a bracket. For instance, column 1, row 3 can be written (1,3). The first number in the bracket always represents the column and the second, the row. (For practice, see worksheet CO-1A, exercise 1.)
Your student should understand that different ways of identifying positions might be used: letters might be used instead of numbers, the numbering might start with 0 rather than 1 (as in exercise 2 on worksheet CO-1A), or the rows might be numbered in increasing order from the top down. Your student should be aware, however, that in all of the applications in this unit, rows are numbered in increasing order from the bottom up.
Finally, your student should understand that a set of positions needn’t always be represented by an array of dots or rectangles. The most useful way to indicate position is to use a grid of vertical and horizontal lines, or a graph (see exercise 3 on worksheet CO-1A). On a graph, the positions are the points where the vertical lines (the columns) meet the horizontal lines (the rows).

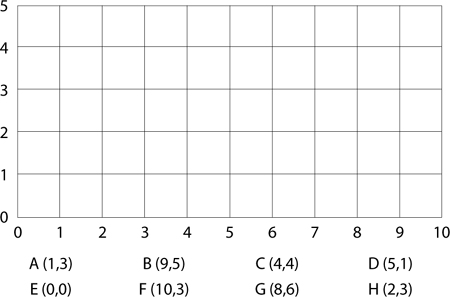
The ordered pairs A (1,3), B (4,2), and C (0,0) represent points located at the positions shown on the graph below:

Sample questions for graphing are given in exercise 3 of worksheet CO-1A. If your student wonders why the numbers on the graph start at 0 rather than 1, tell them that graphs are normally used to represent the position of things relative to a particular starting point. For example, in the map on page 153, the house is placed in the lower left corner of the graph. If you assign this point coordinates (0,0), then the ordered pair associated with the school (3,1) tells you exactly how many blocks you need to travel from the house to get to the school (3 blocks east and 1 block north). That is why it is convenient to give the starting point coordinates (0,0). This point is called the “origin” of the graph.
Your student should also be able to tell you how many rows and how many columns there are in an array. For instance, the following array has two columns and three rows.

When your student has finished worksheet CO-1A, tell them that they are now prepared to understand and perform the card trick.
Ask your student to select a card in the array, then tell you what column it’s in, but not the card. Gather up the cards, with the three cards in the column your student selected on the top of the deck. Deal the cards face up in another 3 x 3 array making sure the top three cards of the deck end up in the top row of the array. Ask your student to tell you what column their card is in. The top card in that column is their card, which you can now identify. Repeat the trick several times and ask your student to try to figure out how it works. You might give them hints by telling them to watch how you place the cards, or even by repeating the trick with a 2 x 2 array.
When your student understands how the trick works, you can ask the following questions:
1. Would there be any point to the trick if the subject told the person performing the trick both the row and the column number of the card they had selected?
Clearly there would be no trick if the performer knew both numbers. Two pieces of information are enough to identify unambiguously a position in an array or graph. This is why graphs are such an efficient means of representation: two numbers can identify any location in two-dimensional space (in other words, on a flat sheet of paper). This discovery, made over 300 years ago by the French mathematician René Descartes, was one of the simplest and most revolutionary steps in the history of mathematics and science. His idea of representing position using numbers underlies a great deal of modern mathematics, science, and technology.
You might ask your student how many numbers would be required to represent the position of an object relative to an origin in three-dimensional space. (The answer is three. Think of the origin as being situated on a plane or flat piece of paper that has a grid or graph on it. You need two numbers to tell you how to travel from the origin along the grid lines on the plane to situate yourself directly above or below the object, and one more number to tell you how far you have to travel up or down from the plane to reach the object.)
2. Would the trick work with a larger array?
Have them try the trick with a 4 x 4 array. They should see that as long as the array is square (with an equal number of rows and columns), the trick works for any number of cards. Ask your student to explain why this is so and why the trick doesn’t work if the array isn’t square (for instance, try it with 2 columns and 6 rows).
The trick can be modified for non-square arrays if you allow one extra rearrangement. Deal out an array of 3 columns, 9 rows. Have your student select a card and tell you what column it’s in. Re-deal the cards so that the nine cards from the chosen column land in the top three rows of the new array. Ask your student to tell you what column their card is in, and re-deal the top three cards in that column into the top row of a new array. Once your student tells you what column their card is in, you can identify the top card in that column as the one they selected.
This version of the trick illustrates a powerful general principle in science and mathematics: when you are looking for a solution to a problem, it is often possible to eliminate a great many possibilities by asking a well-formulated question. In the card trick above, one is able to single out one of 27 possibilities by asking only three questions. Repeat the trick, asking your student how many possibilities were eliminated by the first question (18), by the second question (6), and by the third (2).
3. Ask your student if the original trick (i.e., with a square array) would work if the subject told the performer which row the card was in rather than which column.
Have your student show you how the new trick would be performed. The fact that the trick works equally well in both cases illustrates a very deep principle of invariance in mathematics. In a square array, there is no real difference between the rows and columns. In fact, if you rotate the array by a quarter turn, the rows become columns and vice versa. More generally, once you fix an origin in space, it doesn’t matter how you set up your grid (the lines representing the rows and columns). In all cases, you need only two numbers to identify a position.
More sample questions for graphing are given on worksheet CO-2A. Before your student tries question 2, make sure they can define and draw a square, a rectangle, a triangle, a parallelogram (a figure with opposite sides equal in length, or equivalently, parallel), and a polygon (a figure with any number of straight sides, not necessarily the same length; a square, a rectangle, a triangle, a parallelogram, a pentagon, and a hexagon are all examples of polygons).
On worksheet CO-3A, you’ll find exercises that will help your student learn how to describe the position of one point in relation to another.
Your student should be aware that in question 3 of worksheet CO-3A, the letters and numbers have been placed along the edges of the grid (rather than at points of the grid as in previous excercises) and hence identify entire squares (rather than points).
1. Circle the points in the following positions:
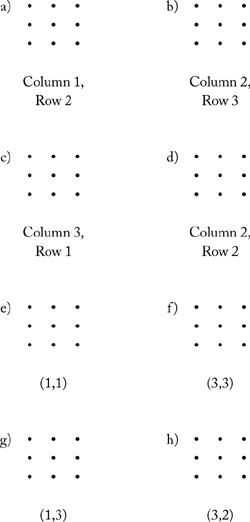
2. Circle the points in the following positions:

3. Put points at the following positions. Label each point with the letter written beside the ordered pair.
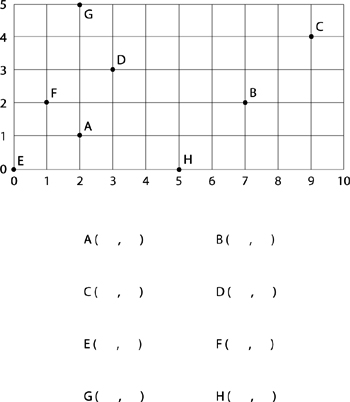
1. Write the coordinates of the following points:
2. Graph each set of ordered pairs and join the dots to form polygons. Identify each polygon.
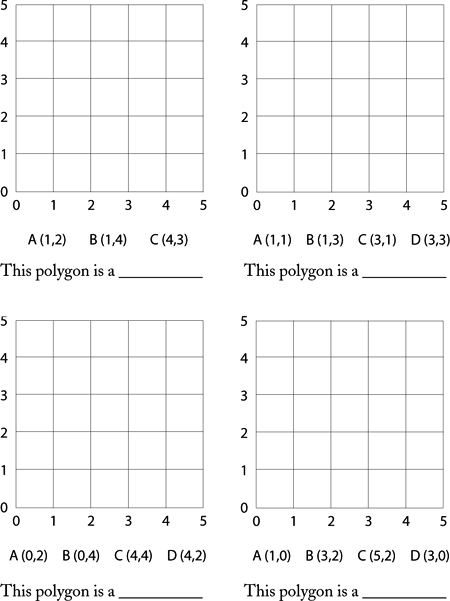
1.
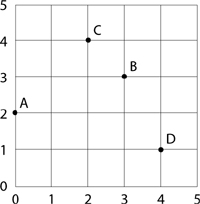
a) What point is 2 right and 2 up from A? __________________
b) What point is 4 left and 1 up from D? ___________________
c) What point is 1 down and 1 right of C? _________________
d) Describe how to get from point B to point D: _________________________________________________
e) Describe how to go to point B from point A: _________________________________________________
f) Describe how to get to point A from point C: _________________________________________________
2.
a) What building is 1 block east and 3 blocks north of the house? _______________________
b) What building is 2 blocks west and 2 blocks north of the school? _______________________
c) What building is 1 block south and 3 blocks west of the school? _______________________
d) Describe how to get from the park to the school: _________________________________________________
e) Describe how to go to the library from the school: _________________________________________________
f) Describe how to go to the park from the library: _________________________________________________
3.
a) What would you find in square (A,3)? ___________________
b) What would you find if you travelled 2 km west of the swamp? ______________________
c) Give the coordinates of the city: ( , )
d) Describe how to get from the city to the lake: _________________________________________________
e) Describe how to get from the mountain to the city: _________________________________________________
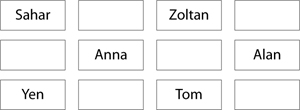
Use the clues to find where the following children sit:
a) Walk 2 desks down and 1 desk right from Zoltan to find John’s seat.
b) Samir is one desk left of Alan.
c) Sally is between Sahar and Zoltan.
d) Walk 2 desks left and 1 desk up from Tom to find Mary’s desk.
e) Tara is one desk right of Zoltan.
f) Noor is between Yen and Tom.