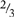).A ratio is a comparison of two numbers.
In the picture, the ratio of circles to squares is 2 to 3. A ratio may be written in ratio form (2 : 3) or in fraction form ().
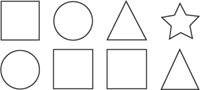
For the diagram above, have your student write, in the ratio form:
a) The ratio of squares to circles (3 : 2)
b) The ratio of stars to triangles (1 : 2)
c) The ratio of circles to stars (2 : 1)
d) The ratio of triangles to figures (2 : 8)
If your student’s reading level is high enough, have them read and answer the following questions (in ratio form):
1. Write the ratio of the number of days in a weekend to the number of days in an entire week.
2. Write the ratio of vowels to consonants in each name:
a) Toronto
b) Montreal
c) London
d) Paris
3. Write the ratio for the value of a penny to the value of:
a) a nickel
b) a dime
c) a quarter
d) a dollar
4. Eleven students tried a swimming test. Five passed on the first try. What was the ratio of those passing to those failing?
5. Using this diagram, write the ratios of the lengths:
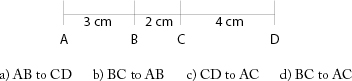
Note: If your student can’t read the questions, you might read them aloud and help your student answer the easier ones.
Ratios, like fractions, may be written in lowest terms. If there are 4 apples in a bowl and 2 oranges, one may say the ratio of apples to oranges is 4 to 2 or, equivalently, that there are 2 apples to every 1 orange. You could illustrate this for your student with a picture:
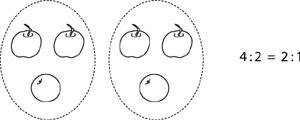
Have your student reduce the ratios as follows:
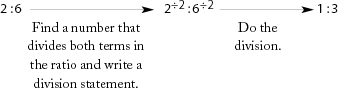
Other examples:
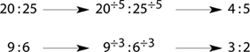
Ask your student to reduce these ratios to the lowest terms:
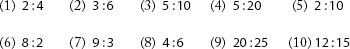
If your student knows other times tables, make up ratios divisible by numbers other than 2, 3, or 5.
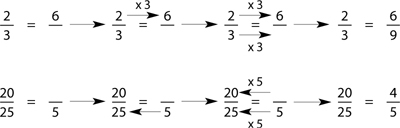
If there are 4 apples for every 2 oranges in a bowl, then there are 2 apples for every 1 orange. The ratios 4 : 2 and 2 : 1 are equivalent. To tell whether a pair of ratios is equivalent, you must first reduce each ratio to lowest terms.
Example: Are 6 : 9 and 10 : 15 equivalent ratios?
The ratios reduce to the same ratio, hence they are equivalent.
Example: Are 3 : 1 and 12 : 9 equivalent ratios?
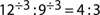
3 : 1 is already reduced to lowest terms and does not equal 4 : 3, hence the ratios are not equivalent.
Have your student reduce the following pairs of ratios to lowest terms and decide whether they are equivalent:
You can make up other examples involving times tables other than 2, 3, and 5. (Note: Order matters in ratios — for example, 1 :3 is not the same ratio as 3 : 1).
In this section, your student will learn how to find the missing number in ratios like:
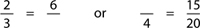
If you give them lots of practice at the steps below, they should find these questions easy.
Step 1: Find the missing number (multiplication).
Have your student fill in the missing numbers for these questions:
(In this section and all subsequent sections, you should make up extra questions involving the times tables your student knows.)
Step 2: Find the missing number (division).
Have your student fill in the missing numbers for these questions:
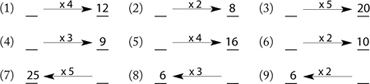
Step 3: Distinguish between the two cases.
Make sure your student knows that if they are given the number at the tail of the arrow they multiply, and if at the tip, they divide. (You might have them say out loud, in each case, “tail,” or “tip” — make sure they know the tip is the pointed end, and that they can distinguish between the tip and the tail no matter which way the arrow is pointing.)
Find the missing numbers:
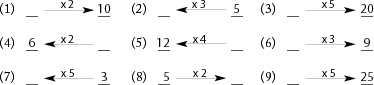
Also make sure your student knows how to check their answer by multiplying the number at the tail of the arrow by the one on top of the arrow to see if they get the number at the tip. You might make up questions in which you have filled in the wrong answer and have your student find your errors. Your student should be able to solve these arrow problems without any difficulty before you proceed.
Step 4: Filling in the arrows.
Make sure you have your student practise each of these steps individually, if necessary.
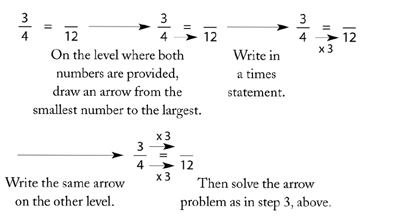
Here are some other examples:
Now, have your student solve these ratios:
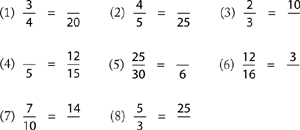
To make up a ratio question, start with a pair of equivalent fractions (e.g.,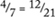 
) then leave one number out (
).
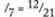Not all ratios can be solved by the arrow method. You can only use the arrow method when the smaller number given divides into the larger. To solve ratios that can’t be solved by the arrow method, you must cross-multiply.
Here is an example of cross-multiplication:
If your student is learning ratios for the first time, stick to questions that can be solved by the arrow method.
If your student is good at long division, you might give them harder questions, such as:
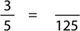
Example: There are 3 cats in a pet shop for every 2 dogs. If there are 12 cats in the shop, how many dogs are there?
Step 1: Write, as a fraction, the ratio of the two things being compared:
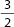
Step 2: Write, in words, what each number stands for:
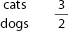
Step 3: On the other side of an equal sign, write the same words, on the same levels:
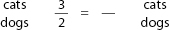
Step 4: Re-read the question to determine which quantity ( i.e., cats or dogs) has been given (in this case, cats) — then place that quantity on the proper level:
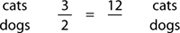
Step 5: Solve the ratio using the method described in section RP-4.
Here are some questions your student can solve:
1. There are 2 apples in a bowl for every 3 oranges. If there are 9 oranges, how many apples are there?
2. There are 3 boys in a class for every 4 girls. If there are 12 girls in the class, how many boys are there?
3. Five bus tickets cost $3. How many bus tickets can you buy with $9?
4. A basketball team won 2 out of every 3 games they played. They played a total of 15 games. How many games did they win? (Note: the quantities are “games won” and “games played.”)
5. To make fruit punch, you mix 1 litre of orange juice with 2 litres of pineapple juice. If you have 3 litres of orange juice, how many litres of pineapple juice do you need?
6. Nora can run 3 laps in 4 minutes. At that rate, how many laps could she run in 12 minutes?
7. The ratio of boys to girls in a class is 4 : 5. If there are 20 boys, how many girls are there?
8. The ratio of the top speed of a lion to the top speed of a hyena is 5 :4. A hyena’s top speed is 64 km/hr. What is a lion’s top speed?
9. Neptune orbits the sun 3 times in the same time it takes Pluto to orbit the sun 2 times. How many orbits does Pluto complete while Neptune orbits 12 times?
10. 2 cm on a map represents 5 km in real life. If a lake is 6 cm long on the map, what is its actual size? (Note: Here the quantities compared are cm and km.)
A percent is a ratio that compares a number to 100. The term “percent” means “out of 100” or “for every 100.” For instance, 84% on a test means 84 out of 100. Tell your student that they can think of percent as a short form for a fraction with 100 in the denominator. For example,
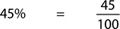
Have your student write the following percents as fractions:
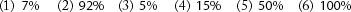
Have your student write the following fractions as percents:
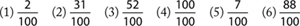
Have your student memorize the following times tables (they should know them really well):
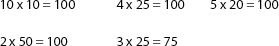
Also make sure that they can multiply numbers with zeroes on the end, for example,
Do not proceed until your student can solve the following arrow problems with ease:
Teach your student to check their answers. Your student can now convert fractions with denominators 2, 4, 5, 10, 20, 25, and 50 to percents using the arrow method (for other denominators they must use cross-multiplication).
Example: Change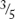 
to a percent.
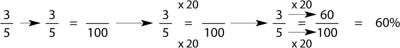
Have your student convert the following decimals to percents (by first converting to a fraction):
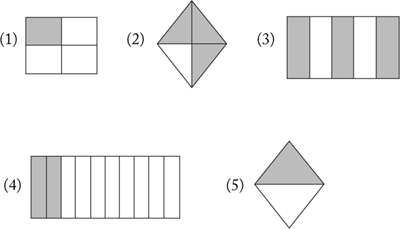
Have your student write the percent of the following diagrams that is shaded:
(This section is for second-year JUMP students)
The sentence “6 is 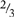of 9” is equivalent to the mathematical expression 
.
Example: Rewrite “8 is 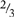of 12” as an equality.
Step 1: Write the fraction given beside an equal sign:
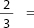
Step 2: Write the number that follows the word “of” on the bottom:
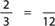
Step 3: Fill in the other number:
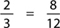
Make sure your student knows that the number that follows the word “of” always goes on the bottom — 12 is the whole that you are taking two-thirds of.
Have your student rewrite the following statements as equalities:
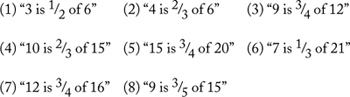
Your student can also write percent statements as equalities.
Example: Write “3 is 75% of 4” as an equality.
First change 75% to a fraction (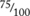
), then use the method above:
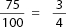
Have your student rewrite the following as equalities:
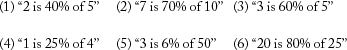
Your student can now find missing numbers in ratios and percent statements.
Type 1: What number is ¾ of 20?
Write the fraction beside an equal sign:
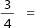
Fill in the number after “of” and solve by the arrow method:
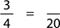
Ask your student to solve the following:
(1) What number is 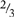of 12?
(2) What number is ¾ of 8?
(3) What number is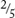 
of 20?
(4) What number is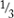 
of 12?
(5) What number is 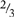of 21?
(6) What number is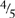 
of 25?
Type 2: 8 is 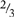of what number?
This time, the number following the “of” is missing (we don’t know the whole of which 8 is two-thirds). Hence the blank goes on the bottom:
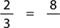
Ask your student to solve the following:
(1) 6 is 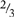of what number?
(2) 15 is ¾ of what number?
(3) 6 is 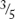of what number?
(4) 10 is 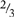of what number?
(5) 7 is 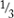of what number?
(6) 9 is ¾ of what number?
Type 3: 4 is how many thirds of 6?
This time we don’t know the fraction:
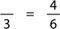
Have your student solve the following:
(1) 8 is how many fifths of 10?
(2) 4 is how many quarters of 12?
(3) 15 is how many quarters of 20?
(4) 6 is how many thirds of 9?
Your student should be able to solve the three types of questions even if they are mixed together:
(1) What number is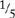 
of 20?
(2) 5 is 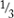of what number?
(3) 9 is how many quarters of 12?
(4) 14 is how many thirds of 21?
(5) What number is 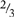of 15?
(6) 6 is 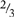of what number?
(7) 10 is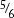 
of what number?
(8) 2 is how many thirds of 6?
Make up other questions of this sort by starting with a pair of equivalent fractions, and then leaving one number out. Make sure your student can articulate, as soon as they have read the question, what is missing — for instance, in the first question above, the part is missing:
In the second question, the whole is missing:
In the third question, the fraction is missing:
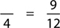
This method also works for percents.
Example: What number is 20% of 5?
Rewrite the percent as a fraction:
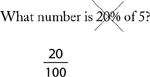
Then solve by arrows:
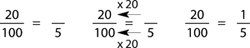
Example: 4 is what percent of 5?
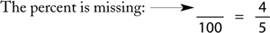
Have your student solve the following:
(1) 3 is 60% of what number?
(2) 4 is what percent of 5?
(3) 7 is what percent of 10?
(4) 1 is 25% of what number?
Make up similar problems by starting with equivalent fractions:
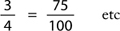
Sometimes your student will encounter slightly different wording:
“Find 20% of 5.”
The word “of” always signals the number that goes on the bottom, for example,
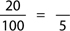
Example: “What percent of 60 is 40?”
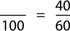
Example: “How many thirds of 9 is 6?”
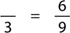
Make up problems with more difficult wording only after your student has mastered the standard wording.