IN MATHEMATICS TEXTS USED IN ELEMENTARY SCHOOLS, STUDENTS are frequently required to solve problems of the following sort: Find all shapes that can be made using five squares (assuming that each square has at least one edge in common with another square). While there are only 12 distinct (non-congruent) shapes that can be made from five squares, there are over 100 ways of drawing or placing the squares without violating the conditions of the question. As teachers are not adequately trained to show a student how to sort through this many possible configurations (and a typical textbook will offer little or no guidance in organizing such a search), an elementary student is unlikely to find all 12 of the shapes that can be made with five squares. They are even less likely to know how to verify whether their set of solutions is complete.
Many discoveries in mathematics are made by the process of elimination: a mathematician lists all of the possible answers to a question (or, more often, the most promising answers), checking to see if any are valid. A knack for solving problems by systematic search is essential in mathematics, but I have never seen a book that isolates this skill. In this unit, your student will learn how to solve problems by listing potential solutions in an organized way.
Note: You needn’t teach this unit all at once — the exercises can be interspersed with other units.
To find a number that satisfies several conditions simultaneously, you can start by making a list of numbers that satisfy one of the conditions, then check to see which numbers on the list satisfy the other conditions. Make sure your student is aware of this rule: you might point out, for instance, that the lists they make in parts g to l of question 2 can be used to solve parts m to u.
Your student should know that the multiples of any number include 0 (e.g., the multiples of 2 are 0, 2, 4, 6, etc.) and that the even numbers also include 0.
1. Write the numbers from 0 to 9 in order.
2. Write all the numbers from 0 to 9 that are
a) greater than 7
b) less than 2
c) greater than 5
d) less than 8
e) greater than 5 and less than 8
f) less than 5 and greater than 0
g) odd numbers
h) even numbers
i) multiples of 2
j) multiples of 3
k) multiples of 4
l) multiples of 5
n) even numbers greater than 7
o) odd numbers less than 5
p) even numbers less than 4
q) even numbers that are multiples of 4
r) odd numbers that are multiples of 3
s) even numbers that are greater than 2 and less than 8
t) odd numbers that are greater than 1 and less than 7
u) odd numbers that are multiples of 3 and greater than 5
3. Write the numbers from 0 to 9 in order, then:
a) Circle the number that is greater than 8
b) Underline the number that is less than 1
c) Cross out the number that is less than 8 and greater than 6
d) Put a check mark over the odd number that is greater than 3 and less than 7
4. Use the clues to find the answers: “I am a one-digit number. I am ...”
a) greater than 8
b) less than 1
c) greater than 6 and less than 8
d) an odd number greater than 7
e) an odd number less than 3
f) an even number greater than 6
g) an even number less than 1
h) an odd number greater than 3, and less than 6
i) an even number greater than 2, and less than 6
k) the second odd number
l) a multiple of 3 greater than 6
m) a multiple of 5 greater than 1
5. Use the clues to find the answers: “I am a two-digit number . ..”
a) My tens digit is 9 and my units digit is 1.
b) My units digit is 5 and my tens digit is 7.
c) My units digit is 0 and my tens digit is 4.
d) My units digit is 5. Both of my digits are the same.
e) My tens digit is 7. My units digit is 2 less than my tens digit.
f) My units digit is 2. My tens digit is 3 more than my units digit.
g) My tens digit is 6. My units digit is 5 less than my tens digit.
h) My tens digit is 7. The sum of my digits is 9.
6. All of these questions have more than one answer. List all of the solutions: “I am a two-digit number ...”
a) The sum of my digits is 2.
b) The sum of my digits is 3.
c) The sum of my digits is 4.
d) The sum of my digits is 5.
e) The sum of my digits is 6.
f) Both of my digits are the same.
g) My units digit is 5. I am less than 40.
h) My tens digit is twice my units digit.
i) My tens digit is 3 times my units digit.
7. All of these questions have only one answer. Read the first sentence and list all possible answers. Then read the second sentence and circle the correct answer: “I am a two-digit number ...”
a) The sum of my digits is 2. Both of my digits are the same.
b) The sum of my digits is 3. My units digit is twice my tens digit.
c) The sum of my digits is 3. My tens digit is greater than 2.
d) The sum of my digits is 4. Both of my digits are the same.
e) The sum of my digits is 5. My tens digit is one more than my units digit.
f) The sum of my digits is 5. My tens digit is 3 less than my units digit.
g) Both of my digits are the same. I am greater than 50 and less than 60.
h) Both of my digits are the same. I am greater than 90.
i) Both of my digits are the same. If you multiply my digits you get 9.
j) Both of my digits are the same. The sum of my digits is 12.
8. All of these questions have more than one answer. In each question there is a sentence that tells you what one of the digits of the answer must be. Underline this sentence. Then write all of the answers. “I am a two-digit number ...”
a) My units digit is 7. My tens digit is even.
b) My units digit is odd. My tens digit is 5.
c) I am between 40 and 50. My units digit is odd.
d) My units digit is a multiple of 3. I am between 70 and 80.
e) I am between 20 and 30. My units digit is a multiple of 3.
f) I am greater than 90. My units digit is a multiple of 4.
g) My tens digit is even. My units digit is greater than 6 and less than 8.
h) My ones digit is odd. My tens digit is greater than 4 and less than 6.
9. What is the hundreds digit of a three-digit number:
a) between 400 and 500?
b) between 200 and 300?
c) greater than 900?
d) less than 200?
10. All of these questions have more than one answer. List all of the answers. “I am a three-digit number .. .”
a) I am greater than 900. My tens digit is 2 times my units digit.
b) I am between 400 and 500. My units digit is 5 more than my tens digit.
c) I am between 200 and 300. My tens digit is 3 more than my units digit.
d) I am less than 200. My tens digit is 4 less than my units digit.
11. All of these questions have one answer. “I am a three-digit number . . .”
a) I am between 500 and 600. All of my digits are the same.
b) I am between 200 and 300. My units digit is 3 times my hundreds digit. The sum of my digits is 10.
c) My hundreds digit, 9, is 3 times my units digit. The sum of my digits is 14.
d) My units digit, 8, is 2 times my tens digit and 4 times my hundreds digit.
e) I am between 800 and 900. My hundreds digit is 2 times my ones digit. The sum of my digits is 15.
f) I am between 800 and 900. My hundreds digit is 4 times my tens digit. The sum of my digits is 14.
g) I am between 300 and 400. My tens digit and my units digit are the same. The sum of my digits is 9.
h) I am between 400 and 500. The digit in each place is one greater than the digit on its left.
i) All of my digits are the same. The sum of my digits is 15.
Advanced
The following questions are more advanced. You might wait until your student is in the second year of JUMP before you cover this material.
In questions 12 and 13, you should tell your student to draw as many lines as there are digits in the number; they can then fill in the blanks using the clues. (Teach your students to put a comma after every three blanks; it will help them see the places.) Your student should know that the units digit of a number is also called “the first digit,” the tens digit is “the second digit,” and so on. The first three digits are “the units period,” and the next three digits are “the thousands period.”
12. The following questions have one answer. “I am a four-digit number . ..”
a) I am less than 2,000. The digits in my units period are all the same. The sum of my digits is 7.
b) All of my digits are the same. The sum of my digits is 20.
d) I am less than 4,000. All of my digits are multiples of 3. My second and fourth digit are the same. My units digit and my hundreds digit are 6 more than the others.
e) My thousands digit is greater than 6 and is 2 times my hundreds digit. My other digits are odd numbers greater than 7.
Before you assign question 13, make sure your student knows the names of the places up to the hundred millions. Point out to your student that when a number has five digits and is less than, say, 40,000, there are several possibilities for the leading digit (i.e., it might be 3, 2 or 1).
13. Answer the following questions:
a) I am a five-digit number less than 30,000. The digit in each place is one greater than the digit on its left. The sum of my digits is 15.
b) I am a number between 400,000 and 500,000. The digits in my thousands period are all the same. The digits in my units period are all the same. The sum of my digits is 18.
c) I am a six-digit number. The digits in my thousands period are all 2s. The digits in my units period are all the same. The sum of my digits is 15.
d) I am a seven-digit number. My millions digit 4, is 2 times my units digit. My thousands digit is three times my units digit. The sum of my digits is 12.
e) I am an eight-digit number between 34 million and 35 million. The digits in my thousands period are all 0s. The digits in my units period are all the same. The sum of my digits is 13.
f) I am a nine-digit, odd number. The sum of my digits is 2.
A mathematician will sometimes gain insight into a challenging problem by inventing a “toy” model of the problem, a version of the problem that has all of the essential features of the original, but fewer elements or parameters. In teaching mathematics, it helps to employ a similar strategy. If my student is struggling with a problem, I will look for a model or sequence of models in which the concepts underlying the problem are isolated or introduced in steps. In this section I present some examples of how I would make toy models to teach more difficult problems.
I recently came across the following exercise in a Grade 8 book: “You have six boxes numbered 1 to 6. Show all the ways you can build two towers three blocks high so that a block with a lower number never appears above a block with a higher number.” If you think your student would have trouble finding (or verifying that they have found) all the solutions to this problem, you could start with the following sequence of questions.
Ask your student to imagine that they have three boxes numbered 1, 2, and 3. Have them draw a picture showing all the ways they could make a stack of two boxes in which a box with a lower number never appears above a box with a higher number. Their answer should have three stacks:

If your student needs help, ask them whether the box with label 3 could ever appear on the bottom of a stack. Point out that they won’t miss any solutions if they proceed in a systematic way. They could put box 1 on the bottom, placing the other boxes on top, one at a time, in order, from least to greatest. Then they could put box 2 on the bottom (and so on, if there are more boxes). Ask your student to use this method to show all the ways they could make a stack that is two boxes high using four boxes (with the rule that a lower number can never appear above a higher number). Then have them list all the ways they can make:
a) a stack two boxes high using five boxes
b) a stack three boxes high using four boxes
c) a stack three boxes high using six boxes
In each of the examples above, I used the numbers on the boxes to help organize my search for solutions. This simple trick (using the order of the natural numbers to list all possibilities) can be employed to solve a wide variety of problems. A student asked to find all pairs of whole numbers that add to 18 might start their list with the number 1 (1 +17 = 18), then the number 2 (2 + 16 = 18), and so on. As long as the student doesn’t skip any numbers in counting, they can be certain they have found all pairs. Similarly, a student asked to find the dimensions of all rectangles with perimeter 18 units (sides are assumed to have lengths that are whole numbers) could begin by calculating the length of a rectangle with width 1 unit, then the length of a rectangle with width 2 units, and so on.
On provincial math tests in Ontario, a great many elementary students fail to find complete solutions to questions of the sort I have mentioned above. I find it surprising that textbooks don’t teach students how to order their search for solutions by counting: once this method is learned it becomes automatic.
Here are several types of questions that can be solved using the ordering method I have described. (All sides of geometric figures have lengths that are whole numbers.)
1. Find the dimensions of all rectangles with perimeter 24 units.
2. Find the dimensions of all rectangles with area 12 units.
3. List the factors of 12. (Ask your student why this question and the previous question have the same set of solutions.)
4. Find the dimensions of all triangles with perimeter 13. (Remember, three numbers can only be the lengths of sides of a proper triangle if the sum of any pair of the numbers is greater than the third number. Hence, 1,1 and 11 cannot be the lengths of the sides of a triangle, as 1 + 1 is less than 11.)
The fourth question is more difficult than the other three. It may be broken into a series of simpler questions. For instance, you might ask: Suppose one of the sides of the triangle has length 3 units. Find all possible lengths for the other two sides.
In elementary schools, students are expected to solve problems of the following type: Find all the ways you can make $1.14 using pennies, dimes, and dollars. If you think your student would have trouble verifying that they have found all solutions to this problem, start with a problem that involves only two types of coins, such as: How many ways can you make 25 cents using pennies and dimes? Tell your student to list their answers in a chart. Your student may discover on their own that the best way to list answers is to start with none of the largest coin (in this case dimes), then one of the largest coin, and so on. Point out that when the number of dimes is fixed, the number of pennies is also determined.
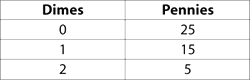
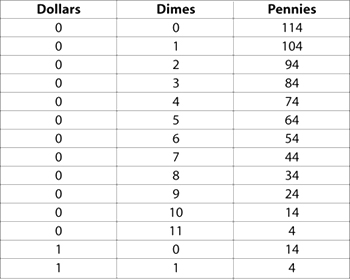
When your student is able to solve any problem involving two coins, they can move on the problem of making $1.14 with pennies, dimes, and dollars. As with problems involving only two coins, it helps to assume that you have none of the larger coin first (so that the problem is reduced to the problem of making $1.14 using pennies and dimes), then one of the larger coin (now the problem is reduced to the problem of making 14 cents using pennies and dimes). As with the previous example, your student can keep track of their answers in a chart:
Problems involving systematic search turn up in every branch of mathematics, including geometry. Here are some simple problems that teach the concepts of perimeter and congruence (two figures are congruent if they have exactly the same shape and size).
1. Write the perimeter of each figure in the sequence (assume each edge is 1 unit).

How does the perimeter change each time a square is added?
If the sequence were continued, what would the perimeter of the seventh figure be?
2. Write the perimeter of each figure in the sequence below:

How does the perimeter change each time a hexagon is added?
If the sequence were continued, what would the perimeter of the sixth figure be?
3. a) Add a square so that the number of exterior edges increases by 2:
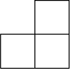
b) Add a square so that the number of exterior edges stays the same:
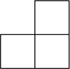
4. Is it possible to add a square to the figure in question 5a so that the number of exterior edges increases by 3 (assuming whole edges must fit together exactly)?
5. Find the perimeter of each figure. Then add one square to the figure so that the perimeter of the new figure is 10 units. (In questions 5 to 8 below, assume all edges are 1 unit.)
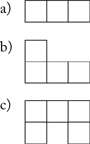
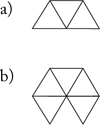
6. Find the perimeter of each figure. Then add one more triangle to the figure so that the perimeter of the new figure is 6 units.
7. Add squares to this figure so that the perimeter is 18
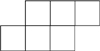
8. Add two squares to the figure so that .
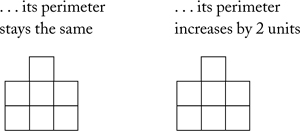
9. Show how many different (non-congruent) shapes you can make by adding one square to the figure. (The square you add must share an edge with a square in the original figure.)
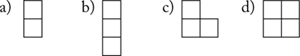
10. Show how many different (non-congruent) shapes you can make by adding two squares.
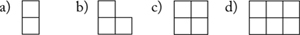
11. How many different shapes can you make using
a) three squares?
b) four squares?
Once your student has successfully completed the exercises above, they should be ready to tackle the problem I mentioned at the beginning of this chapter, namely: Find all shapes you can make using five squares. (Your student should look for solutions to this problem by adding a single square, in various positions, to the figures they made in question 11b.)
As your student becomes more adept at systematic search, you can introduce them to more challenging mathematical puzzles. Here are several examples of puzzles that require a good deal of search by trial and error.
1. Place the numbers 1, 2, 3, 4, 5, and 6 in the boxes and circles so that the number in each circle is equal to the sum of the two numbers in the boxes nearest to the circle.
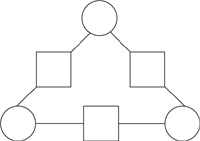
In this question, you can teach your student how to eliminate possibilities before they start: for instance, you might ask, “Are there any numbers that can’t be placed in the circles?” Your student should see that neither 1 nor 2 can be placed in the circles, as no pair of numbers will add to 1 or 2. This means 1 and 2 must be placed in a pair of boxes, and that 3, therefore, must be placed in the adjacent circle.
If you think your student is ready for more challenging work, you could give them the following questions:
2. Place the numbers 1, 2, 3, 4, 5, and 6 so that the three numbers along each edge add to:
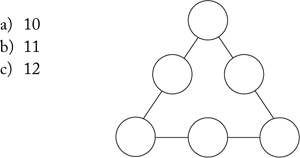
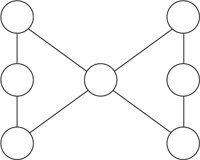
3. Place the numbers 1, 2, 3, 4, 5, 6, and 7 so that the three numbers along each line, including the diagonals, add to the same number.
1. With coins or a picture, show all the ways you can make the following amounts using nickels and dimes:
a) 10 cents
b) 15 cents
c) 20 cents
d) 25 cents
2. With coins or a picture, show four ways you can make the following amounts using nickels, dimes, and quarters:
a) 25 cents
b) 30 cents
c) 60 cents
3. Crayons come in boxes of 4 or 5. For each of the following numbers, can you buy a combination of boxes that will give you the number exactly? (For some of these questions, you needn’t buy boxes of both types.)
a) 8 crayons
b) 10 crayons
c) 11 crayons
d) 14 crayons
e) 17 crayons
f) 18 crayons
g) 19 crayons
h) 21 crayons
i) 25 crayons
4. In each of the following questions, your student should fill in the blanks with the digits from 0 to 9 (in each question, they can only use each digit once). Make:
a) The greatest number____
b) The least number__
c) The least odd number___
d) The greatest number with 9 in the tens place___
e) The greatest even number with 4 in the thousands place
f) The greatest odd number with 7 in the thousands place
g) The least even number greater than 30,000 _____
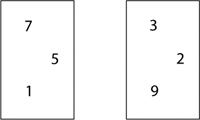
5. Pick two numbers, one from each of the boxes so that:
a) the product of the two numbers is smallest
b) the product is the greatest
c) the product is closest to 20
d) the difference between the two numbers is smallest