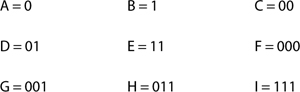
IN THIS UNIT, YOUR STUDENT WILL LEARN HOW TO MAKE A FINITE state automaton, a simple model of a computer, which can be played like a board game. Though the model has no wires or circuits (your student will have to supply the “electricity”), it can perform several of the same functions as a real computer. By feeding code words into the automaton, your student will learn how a computer performs basic tasks, such as identifying patterns in numbers and codes.
Computers follow instructions that are encoded in strings of letters or numbers called “words.” The words that tell a computer what to do are generally written using only two symbols. This is because the presence of an electrical current in a wire or circuit can represent the occurrence of one of the symbols, and the absence of current, the other. The symbols most commonly used in computer science are “0” and “1.”
To give your student an idea of how instructions may be encoded in strings of zeroes and ones, you should write down the following code:
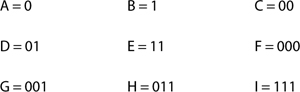
Ask your student to continue the pattern in the code. They should notice that each new “word” in the code is generated either by replacing the rightmost zero of the previous word with a one, or, if the previous word consists entirely of ones, by creating a string of zeroes one longer than the string of ones. Hence, the pattern continues as follows:
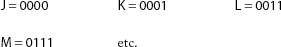
Show your student how to translate a code word into English by writing the corresponding letter of the alphabet under each block of code. For instance,
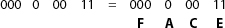
Ask your student to decode the following words:

(If your student enjoys working with codes, have them translate a word that contains letters that occur near the end of the alphabet. This will require extending the code further than what is provided above.)
A binary code is one that uses only two symbols. The code given above is not, strictly speaking, binary, since it allows for a space between blocks of symbols. (From the point of view of a computer, a space is a third symbol.) You might ask your student to think about how they would design a code that does not require a space. Here is an example of such a code:
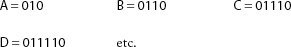
It is easy to spot the letters of the alphabet in words written in binary code, as each letter is represented by a block of ones, flanked by a pair of zeroes. For instance, in “0110010011110” the letters b, a, and d stand out.
Ask your student to simplify the code I have just given. (One way to simplify the code is to drop the final zero in each word: the code still works if A is written 01, B is written 011, etc.)
In the code given above, the word “000000” is meaningless, as it does not correspond to any letter or series of letters in the English alphabet. A computer can only follow instructions that are correctly written in the specific code the computer uses. In order to process and execute instructions, a computer must be able to recognize various kinds of patterns in strings of symbols.
In this section, your student will learn how to design an automaton that can “read” and recognize patterns in binary words. Such automata are important components of most computers.
A finite state automaton consists of a set of circles labelled with numbers, and a set of arrows labelled with the letters “a” and “b.” (Automata with more than two types of labels on their arrows are equivalent in computing power to those with only two types of label, so we will only consider automata of the latter sort.) A circle is called a “state,” while a pair of concentric circles is called an “accept state.” The automaton below has three states. The state labelled with a “0” is an accept state.
In an automaton, exactly two arrows must originate from each state. One of the two arrows must be labelled with an “a” and the other with a “b.” An arrow from a state must either point to another state or to the state where it originated. In the diagram above, the “b” arrow originating at state 0 points to state 2, while the “a” arrow loops back and points to state 0 itself.
Ask your student to copy the finite state automaton given above onto a piece of paper. Place a penny or marker on the zero state of their picture. Then give your student a word written in the letters “a” and “b.” (The states of an automaton are normally labelled with numbers, but I have chosen to write words using the letters “a” and “b,” rather than zeroes and ones: students find this less confusing.) Tell your student to read the word you gave them from left to right, one letter at a time. Each time they read a letter, they should move the penny along the arrow labelled by the letter they have just read. For instance, if you were to give your student the word “baa,” they would move the penny from state 0 to 2, from state 2 to 1, and then from state 1 to state 1 (i.e., on the final move, the penny remains in the same state, because the arrow labelled “a” loops back to that state).
A finite state automaton can either accept or reject a word. Normally, finite state automata are designed to accept only those words that are meaningful or “well formed” in whatever code the computer uses. In our penny model of a finite state automaton, words are accepted or rejected as follows: if, when the final letter of the word is read, the penny lands in an accept state of the automaton, the word is accepted. Otherwise, it is rejected. In the example given above, the word “baa” is rejected, as state 1 is not an accept state.
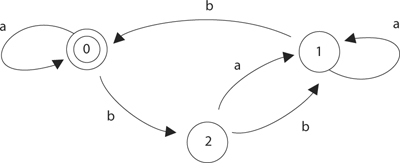
Have your student try other words on the automaton until they get used to moving the penny around as they read a word. You should give them a list and have them check which words the computer accepts. Then show them the following automaton and ask them to try to figure out what kind of words it accepts:
You might give them some hints: for instance, you might point out that an occurrence of “b” in a word always leaves the penny in the same state, since all of the “b” arrows are loops. You might give your student a word with three a’s, then one with six a’s. They should see that the automata accepts any word in which the number of a’s is a multiple of 3 (the number of b’s doesn’t matter). Ask your student to draw an automaton that will accept any word in which the number of a’s is a multiple of 5. Then ask them to figure out what kinds of words each of the following automata will accept.
1.

This automaton accepts words that have an even number of a’s.
2.
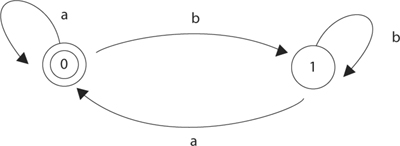
This automaton accepts words that end in one or more a’s.

This automaton accepts words that start with at least two a’s.
The following questions are more advanced:
4.
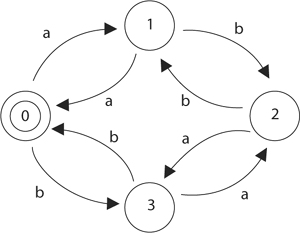
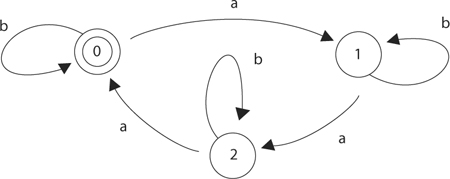
This automaton accepts words that have an even number of a’s and also an even number of b’s.
Automata may also have more than one accept state, as in the following:
5.
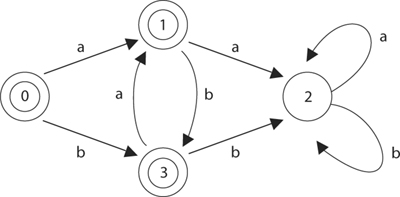
This automaton accepts words that don’t have two a’s or two b’s in a row.
You might ask your student to design their own automaton and, if possible, determine what kinds of words it accepts. The question of what kinds of words automata can recognize is a very deep and important question in computer science.
A finite state automaton may be represented by a set of brackets containing letters and numbers. The brackets and symbols are a code that tells you how to construct a particular automaton. In each bracket, there are three positions. The first position contains a state number, the second a letter (either “a” or “b”), and the third, another state number. For instance, the bracket (1,a,2) means that in the automaton, there is an arrow labelled “a” from state 1 to state 2 (or, interpreted as an instruction, the bracket means that if the penny is in state 1 and you read an “a,” you should move the penny to state 2). A description of an automaton should also specify which of the states of the automaton are “accept” states.
The following “code” gives the program for the automaton on page 197:
(0,a,0) (0,b,2) (1,a,1) (1,b,0) (2,a,1) (2,b,1)
where 0 is the accept state.
Write a code for one of the automata above and ask your student to draw a picture of the automaton from the code. Then have your student write the code for an automaton from its diagram.
Note: Several months ago, after a lesson on finite state automata, my daughter Chloe decided she would make her own model of a computer. She found a shallow box with a Cellophane lid and put a drawing of an automaton inside. Then, rather than using a penny as a marker, she placed a round fridge magnet on the zero state of her automaton and used a second magnet on the back of the box to pull the other magnet around like a cursor. She drew a keyboard for her computer, along with several Web pages and games (mazes and so on). When Chloe demonstrated her model to a Grade 3 class in the JUMP program, all of the kids wanted to make their own computers. I gave them cardboard folders instead of boxes, and they used paper clips to hold their drawings in place while they moved the magnets around. Many of the children mentioned this lesson in their thank-you letters to JUMP: in their minds, they had made real computers.