Analogical Mapping in Numerical Development
Elisabeth Marchand; David Barner University of California, San Diego, CA, United States
Abstract
This chapter outlines the contribution of analogical thinking in numerical cognition and specifically to number-word learning and numerical estimation. We begin with an overview of number-word learning, followed by a description of analogical mapping as defined by Gentner (1983, 2010), and discuss how children might acquire the meaning of counting based on analogical mapping. Next, we review the claim that very similar processes of analogical mapping may support numerical estimation, based on findings from studies of dot-array and number-line estimation. These studies suggest that children's knowledge of how the count list is structured and in particular the ordering and distance between numbers affects their ability to make accurate estimates. Finally, we discuss extensions of this idea to other cases where analogy has been proposed as a source of representational change. We conclude that analogical mappings enrich how humans transcend core numerical abilities to represent abstract content.
Keywords
Analogy; Number acquisition; Successor function; Numerical estimation; Structure mapping
Introduction
Mathematical thinking relies on a wide range of abstract representations that are unique to human cognition. The ability to create abstract numerical representations such as variables, matrices, and infinite magnitudes is related to learning a symbolic number system, beginning with a count list. Humans have created a host of different counting systems, including nonlinguistic systems such as the abacus, tallies, and body-count systems and linguistic systems, like verbal count lists (Ifrah, 2000; Menninger, 1969). Over the past several decades, there has been increasing evidence that language provides an especially powerful tool for representing number, beginning early in a child's life. Studies have shown that the acquisition of a verbal counting system allows children and adults to precisely quantify large sets of objects and that verbal working memory is essential to carry out arithmetic operations (Ashcraft & Stazyk, 1981; Barner, Chow, & Yang, 2009; Dehaene, Spelke, Pinel, Stanescu, & Tsivkin, 1999; Frank, Everett, Fedorenko, & Gibson, 2008; Gordon, 2004; Pica, Lemer, Izard, & Dehaene, 2004). However, the precise role of language and the mechanisms by which it is related to nonverbal numerical representations remains controversial.
In this chapter, we argue that a key component to the human ability to represent number with natural language is what Gentner and colleagues (Forbus, Gentner, & Law, 1995; Gentner, 1983; Gentner & Markman, 1997) have called “analogical mapping,” defined as the construction of correspondences between two representations that share similar structures. Specifically, we review evidence that both the acquisition of number words and their use when estimating large sets depend fundamentally on the construction of analogical mappings between language and nonverbal representations. To support the claim that number-word learning relies on analogical mapping, we analyze Carey's (2004, 2009) account of number learning, address the problems with this account, and offer alternatives for how children acquire the meaning of counting based on analogical mapping. Second, we argue that very similar processes of analogical mapping support numerical estimation—for example, the labeling of large sets of rapidly presented objects. To make this claim, we review evidence from calibration effects during estimation and from the role of ordinality in the representation of symbolic numbers. We conclude that analogy is key to understanding how perception and language become related in development and how this allows humans to acquire fundamental mathematical knowledge.
Analogical Mapping in Integer Learning
The central aim of this chapter is to understand how language becomes related to nonverbal numerical knowledge and whether mapping numerical content to language fundamentally changes the types of numerical thoughts humans can entertain. Our proposal is that learning the meanings of number words and learning how to rapidly assign labels to large arrays of objects when estimating both rely on the so-called analogical mapping. In this first section, we explore the role of language and analogical mapping in the acquisition of counting logic and the concept of natural numbers.
Acquisition of Natural Numbers
A central challenge when children learn how to count is the problem of discovering how counting represents cardinality. Studies of number-word learning have found that it is indeed a difficult process that takes place over the course of many years. In the United States, English-speaking children typically begin by learning the count list at around the age of 2 as though it were a single expression, much like the alphabet (one two three four…), and at this point attach no meaning to the individual words (Carey, 2001; Carey & Sarnecka, 2006; Le Corre & Carey, 2007; Wynn, 1990, 1992). For example, if a child is asked, “how many objects are there?”, they may be able to point at the objects while reciting the count list but nevertheless fail to recognize that the last number word in the count sequence represents the total amount of objects in the set (Fuson, 1988). Also, if asked to give a particular number of objects—even a small number like one or two—children at this stage often give random amounts. When children do begin to associate number words with meanings, they do so in sequence, learning the meanings of one, two, three, and four in order over many months (Le Corre, Van de Walle, Brannon, & Carey, 2006; Sarnecka & Carey, 2008; Sarnecka & Lee, 2009; Wynn, 1990, 1992).
This sequence has been demonstrated using the give-a-number task, in which children are asked to provide N number of objects (e.g., “can you give me four marbles?”; Fuson, 1988; Wynn, 1992). Sometime, after beginning to recite the count list, children who are asked to give one object are able to give one, and do not give one for larger numbers. However, they are unable to reliably give appropriate amounts for larger numbers like two, three, and so on. These children are often called “one-knowers.” Around 6–9 months later, children learn an exact meaning for two and can give one and two objects when asked for one and two but give incorrect responses for larger numbers. These children are generally called “two-knowers.” Next, children become “three-knowers” and sometimes “four-knowers.” Finally, after learning three (and sometimes four), children appear to make a remarkable breakthrough: they seem to realize that the last number word used when counting objects refers to the cardinality of the set and can use their counting routine to generate and give sets larger than three or four. At this stage, children are referred to as “cardinal-principle knowers” (CP-knowers).
By some accounts, becoming a CP-knower involves learning the logic of counting and in particular the successor function. The Peano-Dedekind axioms, which describe the core logical foundation for natural number and arithmetic, define the successor function as including a combination of (1)–(3):
- 1. One is a natural number.
- 2. For every natural number n, the successor of n is a natural number.
- 3. Every natural number has a successor.
The successor function sits at the core of natural number because it defines all possible numbers. For children, acquiring it requires learning that, for any number, no matter how large, a larger number can be created by adding “one” and, following this logic, that numbers are infinite (for discussion, see Cheung, Rubenson, & Barner, 2017).
As we discuss in the following section, a number of researchers, including Carey (2009), have proposed that children become CP-knowers when they notice that the successor function describes the relations between the numbers one, two, and three. On Carey's account, this conceptual change is the product of a type of analogical mapping between relations among number words and relations among cardinalities.
Analogical Mapping in Acquiring Natural Numbers
In the present section, we begin by defining what we mean by analogical mapping, describe Carey's account of how analogy might guide the acquisition of the successor function (e.g., as per Carey, 2009), and argue that, while Carey is right to invoke analogy in this case, she is likely incorrect about when children learn the successor function and thus which information they use to do so.
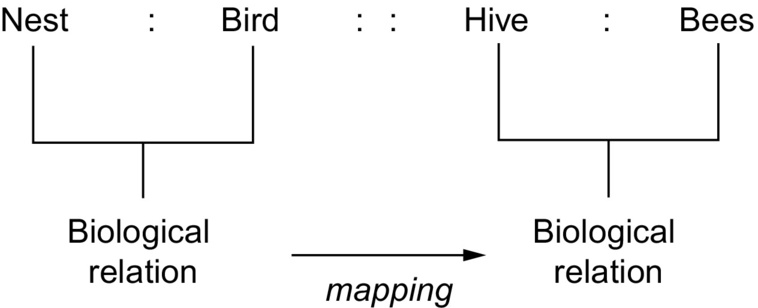
According to Gentner's (1983) “structure-mapping” theory, learning abstract concepts like number words often involves a process of establishing a structural alignment between two representations—a base and a target—and then projecting inferences from the base to the target (and vice versa). To illustrate how structural alignment is deployed and how children can learn from analogical mapping, we present here an example similar to the stimuli used by Goswami and Brown (1990): nest:bird::hive:bee or in common language “a nest is to a bird what a hive is to bees.” In this example, the analogical mapping aligns two distinct instances of a biological relation—that between an animal and its corresponding habitat. Since the child is more likely to be familiar with birds and nests, they are also more likely to discover the relation between the two elements: that nests are the habitats of birds where they lay eggs. The relation nest:bird can therefore constitute the base of the structural alignment. In contrast, the relation between bees and hives, which the child is less familiar with, constitutes the target.
The structural alignment takes place as the child notices that the two biological relations share an isomorphic structure: the two elements of the base and the target—animal and habitat—can be put into correspondence such that the two animals go with their two habitats (Fig. 1). Spontaneously, the child can compare the two biological relations and find the similarities and differences between them. For instance, whereas hives contain the bee's food source (honey), nests do not contain the chick's food source. This comparison process allows the child to make inferences about the target (hive) from what he knows about the base (nest), for example, that the hive houses bee eggs. From this analogical mapping, the child can also discover abstract, less obvious commonalities between many animal species (e.g., that most animals build habitats that are adapted to their needs in order to raise their offspring). This example illustrates how analogical mapping can promote learning: it supports abstraction, highlights differences and common underlying relational structures, and facilitates inferential thinking and the transfer of information between two representations.
According to Wynn (1992) and Carey (2004, 2009), analogy plays a similar role in children's discovery of the successor function. On this view, children begin by learning small number words via item-based associative mappings between the words one, two, three, and four and representations of small sets. For Carey, these small sets are represented by what she calls “parallel individuation” (PI) system, which allows human to keep track of three to four individual objects in parallel and to compare sets via one-to-one correspondence.1 Once children store associations between the number words one, two, and three and the sets that they represent in long-term memory, they are in a position to “make a wild analogy—that between the order of a particular quantity within an ordered list and that between this quantity's order in a series of sets related by additional individuals” (Carey, 2004, p. 67)—or what Wynn (1992) described as “the analogy between the magnitudinal relationships of their own representations of numerosities and the positional relationships of the number words” (p. 250).
In other words, children notice that the labels for small numbers (1, 2, and 3) comprise an ordered sequence and that this sequence is isomorphic to the ordered sequence of quantities that the words denote; specifically, each step forward in the count list corresponds to the addition of exactly one to the cardinality of the set (Fig. 2). According to Carey, “if the child recognizes this analogy, she is in the position to make the crucial induction: for any word on the list whose quantificational meaning is known, the next word on the list refers to a set with another individual added” (Carey, 2001, p. 67). Based on this, Carey argues that children next infer that this parallel increase of one holds for all numbers in the count list, an inductive generalization that is confirmed with experience counting larger numbers. Hence, according to Wynn (1992) and Carey (2001, 2004), analogical mapping allows children to acquire the logic that governs number words (successor function), which not only determines the cardinalities of all number words but also provides the logical foundations on which to build other mathematical knowledge.

Problems With the Current Account of Analogical Mapping in Integer Learning
According to Carey's (2004, 2009) account, children form an analogy between the count list and representations of small sets, which allows them to discover the successor function. On this account, children who have made this analogy understand the cardinal principle—that is, the last word in a count labels the cardinality of the counted set—and are thus referred to as CP-knowers. One problem with this theory is that, according to recent studies, many children classified as CP-knowers do not appear to have knowledge of the successor function (Cheung et al., 2017; Davidson, Eng, & Barner, 2012). Below, we review the original evidence that supported Carey's account and describe in more detail the problems with this account.
As evidence for the hypothesis that becoming a CP-knower is driven by acquiring the successor function, Sarnecka and Carey (2008) tested 2- to 4-year-old children with what they called the “unit task.” In this task, an experimenter places a set of objects into a box and labels it with a number word—for example, “OK, I'm putting FOUR frogs in here.” Next, they add either one or two more objects to the box and ask children how many there are in a two-alternative forced choice task—for example, “now, is it FIVE or SIX?”. Overall, Sarnecka and Carey (2008) found that, whereas subset knowers (one-, two-, three-, and four-knowers) performed at chance and chose randomly between the two options, CP-knowers selected the correct number 67% of the time, on average. Based on these results, they concluded that CP-knowers, but not subset knowers, have knowledge of the successor function, and therefore, learning the successor function is what causes children to become CP-knowers.
However, there are several problems with this conclusion. First, most of the CP-knowers in Sarnecka and Carey's (2008) study (16 out of 29) did not perform better than chance on the unit task. If mastery of the successor function were really what caused children to become CP-knowers, then we should expect them to be able to identify successors relatively systematically either before or at the moment they become CP-knowers. The fact that most children failed suggests that children may not learn the successor function until after they become CP-knowers. Second, whereas Sarnecka and Carey (2008) claimed that children had made an inductive inference—that is, an inference that applies to all numbers—they only tested very small, familiar numbers, making it possible that the small group of CP-knowers who did succeed at the task only did so because they had learned item-specific knowledge regarding the difference between, for example, four and five. To demonstrate that children have made an inductive inference over all numbers, much stronger evidence is required and at the least evidence that children can perform the task for more than one or two small numbers.
To explore these issues, Davidson et al. (2012) presented CP-knowers with different tasks measuring their knowledge of the order of numbers in the count list, the successor function (via the unit task used by Sarnecka & Carey, 2008) and the count list. Overall, the authors found that most CP-knowers didn't know which of two numbers in their count list denotes the greater quantity and most importantly failed to understand the + 1 rule for even very small numbers such as 5 or 6 (well within their counting range). Interestingly, performance on the unit task (which probed the successor function) was related to children's knowledge of the count list—a proxy for experience counting: children who could count up to 19 or less performed at chance for small numbers like 4 and 5, while children who could count up to 30 showed a better understanding of the relation between small numbers but were nevertheless at chance for numbers in the teens. Only the highest counters, who could count to 30 or more, performed well for small numbers, though these children continued to struggle with numbers greater than 10, even though these numbers were well within their familiar counting range. Together, these findings suggest that CP-knowers have difficulty generalizing the successor principle to all numbers within their productive counting range, as an inductive inference account would predict. In other words, knowledge of the successor function does not arise when children become CP-knowers. Instead, according to Davidson et al. (2012), becoming a CP-knower appears to involve learning simple procedures for counting and constructing sets but with very little insight into how or why this works.
While Davidson et al. (2012) showed that young CP-knowers have not yet learned the successor function, their study did not describe when children learn this knowledge nor how. In fact, as noted by Cheung et al. (2017), the unit task is not an appropriate measure of this knowledge when used in isolation, because the task does not measure the successor function as it is typically defined. In past studies, the successor function is generally defined as a relation between numbers—for example, that the successor of a particular number n is defined as n + 1. Critically, however, the successor function as defined in the Peano axioms states that for any number, n, this number has a unique successor whose value is n + 1, such that there is no highest number. This means that in order to have a complete understanding of the integer concept, children must learn that all numbers have a successor and thus that numbers never end. Thus, Sarnecka and Carey's (2008) study was limited not only by the relatively small range of numbers that they tested but also by the fact that the unit task is limited to probing a finite set of numbers—that is, whichever numbers children happen to be familiar with.
In an effort to address this problem, Cheung et al. (2017) presented 4- to 6-year-old children with the unit task of Sarnecka and Carey (2008) and an infinity task—a set of open-ended questions that tested whether children thought all possible numbers have a successor (adapted from Evans, 1983; Hartnett & Gelman, 1998). In this task, children were asked, for example, “What is the biggest number you can think about?”, “If I keep counting, will I ever get to the end of numbers, or do numbers go on forever?”, and “If we thought of a really big number, could we always add to it and make it even bigger, or is there a number so big, we couldn't add any more?”. Cheung et al. (2017) found that CP-knowers' ability to identify successors was highly variable and depended upon their age and their counting skills, such that experienced counters, who are also older, are more likely to find a successor for a presented number and know that every number n has a successor n + 1. In the infinity task, only 24 out of 100 CP-knowers judged that it is possible to always add 1 to a number and that there is no largest number. In light of these results, the experimenters concluded that it is only after becoming CP-knowers and mastering numbers up to around 80 that children develop a complete understanding of the successor function, which occurs sometime between 5½ and 6 years of age. These findings also suggest that children only have item-based knowledge of the successor function when they become CP-knowers and that experience counting to large numbers may contribute to learning the successor function.
How can these findings be reconciled with the account proposed by Carey (2004, 2009)? As explained by Cheung et al. (2017), their data pose a problem to Carey's analogical mapping account only if we assume, as Carey does, that the successor function is acquired from an induction over mappings between small sets and their labels. However, it is also possible that the same mechanism operates over different input available to children after they become CP-knowers. As described in Cheung et al., after becoming CP-knowers, children continue to be exposed to large numbers and are placed in various situations where they have to count large quantities. At this point, CP-knowers have access to a counting procedure (i.e., the ability to generate sets of any sizes), which provides them with the opportunity to place numbers in an isomorphic relation with many different cardinalities, thus allowing them to notice that larger numbers, like small ones, are related by a difference of 1. This broader range of experience may allow children to infer that the successor function holds across their productive count list. Furthermore, as children acquire new sequences of the count list, they may become more likely to notice the recursive structure of the count list (e.g., that the same units from one to nine are repeated within every decade). Given such an observation, children would then be in the position of knowing (1) that the successor function applies to all words in their known count list and (2) that the count list has a recursive structure and thus can be extended indefinitely. Together, these observations may allow them to infer that an infinite number of numbers are related by the successor function.
An alternative possibility is that children do not discover the successor function themselves but instead acquire it chiefly through explicit instruction, when they begin to learn arithmetic in school. At around 5½ to 6 years old—around the time that Cheung et al. (2017) argued that children learn the successor function—children begin to receive exposure to explicit arithmetic facts, like 4 + 1 = 5 and 5 + 1 = 6. These facts, which are directly relevant to acquiring the successor function, might alone serve as the inputs to acquiring the broader generalization that the successor function applies to all numbers, without direct appeal to the representations of perceptual magnitudes. For example, having learned that 1 + 1 = 2, 2 + 1 = 3, 3 + 1 = 4, etc., children might form the generalization that for all n, n + 1 = S(n)—i.e., that adding 1 to a set labeled by the word four produces a set labeled by the successor of four in the count list. Whereas the first alternative is based on an analogical mapping, this second alternative for how children acquire the successor function does not.
A third possibility is that a complete understanding of the successor function might be supported by a combination of different types of information. It is possible, for example, that counting experience enables children to learn, via analogical mapping, that the successor function applies to all possible sets that they can count (since a count of 9 and a count of 10 differ by exactly 1, just as all counts that differ by one numeral). This might allow the child to extend the successor function to the largest number or set that they can think of, which, assuming the child cannot imagine infinite magnitudes, might be limited to a hypothesis space of finite sets and finite number words. To transcend this, children might need to learn a set of rules that consider numbers as distinct abstract entities, disconnected from perception or the count list, which might support the intuition that numbers can be added endlessly—for example, as is the case with arithmetic. Counting experience and memorizing arithmetic facts are two situations that have similar structure: They rely on learning procedures and constructing isomorphisms between these procedures and cardinalities in the world—for example, that the equation 2 + 2 = 4 is isomorphic to a situation in which two sets of 2 are combined to create a set of 4. By noticing this isomorphism and thereby making an analogical mapping between symbols and sets, children might learn the successor function directly from arithmetic. On this hypothesis, the successor function might be learned from a combination of analogical mapping and experience with formal mathematics.
In summary, while several alternative accounts remain viable regarding how children learn the logic of counting, most have one aspect in common: they rely, at least in part, on analogical mapping. Future studies should test the predictions made by these three accounts to determine the specific experience and knowledge needed for this analogical mapping: counting with large numbers, recursive count list, and/or memorizing arithmetic facts. In the next section, we argue that analogical mapping plays an additional crucial role in numerical cognition: allowing children to build relations between verbal and nonverbal systems of approximate numerical representation.
Analogical Mapping in Magnitude Estimation
As children learn to count, they also begin to associate number words with large sets in parallel, allowing them to make rapid estimates without counting. For example, without counting, 5-year-old children can give nonrandom verbal estimates for large sets, though these estimates follow a logarithmic pattern early on, and become more linear at ages 6 and 7 (Barth & Paladino, 2011; Lipton & Spelke, 2005; Mundy & Gilmore, 2009). How do children construct this mapping between the verbal and nonverbal number systems? One possibility is that these systems become related to each other via associative learning (i.e., item-based association between number words and their magnitude). However, in this section, we propose that the same analogical mapping mechanism that is involved in acquiring the logic of counting also supports children's developing ability to make estimates of large sets. Specifically, in this section, we provide two pieces of evidence in support of the idea that the count list and nonverbal representations are related via an analogical mapping during estimation. First, we present findings revealing the considerable flexibility and interdependence of participants' responses when estimating. This evidence suggests that number words are not rigidly associated to numerical magnitudes in an associative, item-based way but instead that children construct a holistic, analogical mapping between the list as a whole and the ordered set of nonverbal magnitudes. Second, again consistent with the idea that there are no item-based associations between the linguistic and nonlinguistic number systems, we discuss evidence that ordinality is essential to the representation of symbolic numbers. Finally, we relate facts regarding two different types of estimation tasks—number-line estimation in addition to dot-array estimation—which provide converging evidence of the role of analogical mapping in estimation processes.
Analogical Mapping in Estimation: Evidence From the Flexibility and Interdependence of Estimates
The approximate number system allows us to represent numbers in a nonsymbolic format (see Feigenson, Dehaene, & Spelke, 2004, for a review), and major accounts agree that the approximate number system is involved in the process of estimation (Booth & Siegler, 2006; Dehaene, Piazza, Pinel, & Cohen, 2003; Le Corre & Carey, 2007), though the exact role of the ANS in the computation often remains disputed. Here, we propose that verbal estimation is based on an analogical mapping between the count list and the ordered set of nonverbal numerical magnitudes encoded by the approximate number system.
The linguistic and nonlinguistic number systems share an isomorphic structure, which is favorable to the elaboration of a holistic, broad, analogical mapping. For instance, both the count list and the nonverbal number system represent increasing ordinal magnitude; the number word 50 comes after 25 just as a set of 50 objects is more numerous than a set containing 25 items. Moreover, both representations encode relative distance and proportions between symbols and approximate magnitudes. For example, the number word 50 is twice the distance from 25 in the count list, just as a set of 50 objects is twice as large as a set of 25.
According to the analogical mapping hypothesis, mappings between the constituents of the two systems are holistic. In the case of estimation, this means that there are no individual associations between specific words but instead one single mapping between the entire count system as a whole and the magnitude system as a whole. Critically, this idea makes strong predictions about estimation behavior: if estimation is driven by a global analogical mapping where one system is associated to another, then learning about one number word would be expected to influence all other number words. In contrast, if number words were individually associated with magnitudes, we would expect feedback about one number word to be relatively independent of feedback for another number—that is, we would not expect the structure of either the count list or the magnitude system to play a role in calibrating these associations. To tease apart these two accounts, Sullivan and Barner (2013, 2014) used a method developed by Izard and Dehaene (2008), whereby adults were presented with rapidly flashed arrays of dots and were asked to produce a verbal estimate of the total number of dots. In the absence of feedback, participants' estimates were largely inaccurate, underestimating the actual numerosity, but their estimates nevertheless increased with numerosity. Interestingly, when feedback (whether correct or misleading) was provided to the participants for a single dot array—for example, telling them that an array of 25 dots contained 50 items—estimates shifted considerably not only for the trained dot array but also for a wide range of numbers. The fact that all estimates were shifted as a group supports the idea of a broad mapping between the entire count list and perceived magnitudes and speaks to the major role that analogical thinking plays in the representation of large quantities.
Several recent studies suggest that, across development, both adults and children rely on an analogical mapping between the count list and the nonverbal representations of number while also building associative item-based mappings for a handful of small numbers. Sullivan and Barner (2013) asked adult participants to estimate flashed arrays of dots but told them before the experiment that there would be an upper limit on the number of dots they would see. Critically, although this limit was actually always 350 dots, different groups were told that they would see up to 75, 375, or 750 dots. Participants were also presented with a number-matching task in which they heard a number word and then saw two arrays of dots presented sequentially and had to judge which array best matched the word. Sullivan and Barner (2013) showed that for small magnitudes (up to about 12), participants matched number words to arrays very accurately and were highly resistant to calibration, whereas for larger sets they were highly influenced by misleading calibration and struggled to correctly match number words to arrays despite the fact that the quantities always exhibited a highly discriminable 2:1 ratio. From these findings, the authors argued that estimation depends on a combination of associative mappings—individual words mapped to their specific magnitudes, which support small numbers—and analogical mapping (or “structure mapping”), which support estimation for larger numbers. In a similar study with children, Sullivan and Barner (2014) found a similar pattern of results: children exhibited strong item-based associative mappings for small numbers (up to around six) but relied primarily on structure mapping when making estimates for larger numbers.
Besides, making predictions about malleability, the structure-mapping hypothesis also makes a second prediction: because of the interdependency of the number-word mappings, the magnitudes and verbal estimates of previous trials should influence the responses for successive trials. Two different studies tested this prediction (Cicchini, Anobile, & Burr, 2014; Vul, Barner, & Sullivan, 2013). In the first study, Vul et al. (2013) presented adults with a calibrated dot-array estimation task and a noncalibrated task and showed that even if participants are not given explicitly misleading feedback, their estimates are mutually constraining, such that estimation error carries forward from trial to trial. From these findings, the authors claimed that the variability found in estimation arises from the variability in the mapping function that connects the verbal and nonverbal number systems. Using a similar logic, Cicchini et al. (2014) measured intertrial dependency and demonstrated that any particular current response was influenced by up to 15% by the immediately preceding response. Again, this suggests that participants' estimates are based on a dynamic process that is more consistent with an analogical account than with associative mappings.
Studies using the number-line paradigm also provide evidence for the analogical mapping hypothesis. In a typical number-line task, participants are presented with a black horizontal line, most frequently marked at the beginning and the end by two numerals (e.g., 1 and 100), and are asked to mark the proper position of a given number. Early studies using this technique found that young children (e.g., 5 years of age) have nonlinear representations, spacing out estimates for small numbers on the line in a relatively linear way but making logarithmic estimates for larger numbers. In contrast, older children (e.g., 7-year olds) make more linear estimates (Booth & Siegler, 2006; Opfer & Siegler, 2007; Siegler & Booth, 2004; Siegler & Opfer, 2003). Recently, additional studies have argued that in these tasks, children estimate using a form of proportional reasoning that resembles analogical mapping, rather than reliance on linear versus logarithmic number representations as previously believed (Barth & Paladino, 2011; Barth et al., 2016; Cohen & Blanc-Goldhammer, 2011). Using the number-line paradigm with children aged 6–8, Barth and Paladino (2011) showed that patterns of estimation were better explained by a proportion-judgment model than a linear model. In a more recent study, Rouder and Geary (2014) developed a set of hierarchical statistical models to contrast the pattern of variability in number-line placements predicted by different theories of number-line representation. Most first graders' placements suggested the use of end points, compatible with the proportional reasoning view. Also, as children got older (fifth grade), their pattern of estimates reflected the incorporation of a midpoint anchor and thus a modified proportional reasoning strategy. Like analogical mapping, proportional reasoning is based on an understanding of the order and the distance between the number words of the count list: for example, if a child knows that 50 is between 1 and 100 and that 100 is twice as far as 50, he can infer quite easily the position of 50 on the number line.
Analogical Mapping in Estimation: The Role of Ordinality
Thus far, we have argued that analogical mapping links the verbal and nonverbal number systems during estimation. This account makes one additional prediction that we explore here. Specifically, it predicts that familiarity with the count list and in particular familiarity with how the list is structured should affect children's estimation performance, since analogical mapping is fundamentally a process of aligning structures from different domains of knowledge.
Previous studies suggest that estimation abilities are strongly related to children's knowledge of the symbolic system and how it is structured (Ebersbach, 2016; Ebersbach, Luwel, Frick, Onghena, & Verschaffel, 2008; Le Corre & Carey, 2007; Lipton & Spelke, 2005). For example, Lipton and Spelke (2005) presented 5-year-old children with three tasks that tested their knowledge of the count list. In a free estimation task, children who were classified as skilled counters produced estimates that were linearly related to numerosity, unlike children classified as unskilled counters. In the number-word comprehension task, where children had to choose which set corresponded to a given number word, only skilled counters were able to perform the task above chance level for small and large numbers. Finally, in the number ordering task, children had to estimate an array of dots based on the cardinal value of one array presented simultaneously. As expected, skilled counters were able to produce ordinal responses—response in the right direction—unlike unskilled counters.
Consistent with the analogical mapping hypothesis, these results suggest that knowledge of the count list is fundamental to estimation. However, this is of course compatible with any alternative accounts, including associative mapping. A unique prediction made by an analogical mapping account is that structural knowledge of the count list should be especially important. Consistent with this, previous studies have found that ordinality is key to understanding how numbers are represented symbolically (Lyons & Ansari, 2015; Lyons, Ansari, & Beilock, 2011; Lyons & Beilock, 2009, 2011, 2013; Roggeman, Verguts, & Fias, 2007; Turconi, Campbell, & Seron, 2006). For example, Lyons et al. (2011) asked participants to compare magnitudes expressed in different formats—that is, arrays of dots, Arabic digits, and verbal numbers. The authors showed that mixing representational formats (such as arrays of dots and Arabic digits) increased reaction times, suggesting that symbolic representations do not automatically trigger representations of quantity. These results are compatible with the analogical mapping view in which the mappings between the linguistic and nonlinguistic number systems are dynamic and rooted in an understanding of the structure of the count list, rather than being driven by automatic, item-based associations between number words and approximate magnitudes. As noted by Lyons et al. (2011), “a crucial facet of numerical symbols is how they relate to other symbols; indeed it may even be the case that with repeated exposure to numerical symbols, symbol-symbol relations in literate adults come to usurp symbol-quantity relations” (p. 1515).
Relatedly, as part of their investigation of analogical mapping in estimation, Sullivan and Barner (2014) explored the relation between ordinal knowledge and estimation abilities in 5- and 7-year-old children. The authors presented children with an ordinality task (e.g., which is more, 20 or 40?) and an estimation task (dot arrays). In the estimation task, children's responses tended to be ordinal (i.e., in the correct direction relative to previous estimates) regardless of estimation accuracy, suggesting that knowledge of ordinality is a precursor to accurate estimation. Moreover, accuracy at the ordinality improved substantially with age. Interestingly, the authors did not find a relation between accuracy in the verbal ordering task and the likelihood that a participant would provide an ordinal response on the estimation task. The authors suggested that “although possessing ordinal number-word representations is a prerequisite for forming structure mappings (or analogical mappings), the presence of relatively good verbal ordering does not ensure that estimates will be ordinal” (Sullivan & Barner, 2014, p. 1751). However, this study used only one task of ordinal knowledge, and further work is needed to shed light on the relation between ordinal knowledge and estimation accuracy.
Other Evidence of Analogy as a Source of Representational Changes
In addition to linking number words to approximate magnitudes, analogy may also play additional roles in the creation of adult-like estimation abilities. For example, Thompson and Opfer (2010) propose an interesting case in which children might analogically extend knowledge of small numbers to inform estimates for much larger numbers. They first evaluated second graders' number-line estimation with lines of identical physical length but that represented the scales of either 0–100, 0–1000, or 0–10,000. On this first task, children's estimates exhibited a linear pattern of estimates on the 1–100 scale but a logarithmic pattern on both of the larger scales. Next, they asked whether explaining the similarities between the more familiar, smaller scale (0–100) and the less familiar scales (0–1000 and 0–10,000) might invite children to form an analogy between the two types of scale and thereby improve their estimates for the larger scales. Consistent with this, they found that after training, children's pattern of estimates on the larger number lines became linear. This suggests that, besides creating an initial link between number words and magnitudes, analogy may also play an important role in gradually extending knowledge of small numbers to larger ones, as children come to understand how the count list is structured.
General Conclusion
In the current chapter, we explored the role of analogical mapping, as defined by Gentner (1983, 2010), in numerical development. We argued, following past accounts (Carey, 2009; Wynn, 1990, 1992), that analogical mapping contributes considerably to the acquisition of the logic of counting but that this learning takes place much later than generally assumed and using different inputs than proposed in previous studies. Also, based on arguments provided by Sullivan and Barner (2013, 2014), we argued that the same mechanism of analogical mapping is also involved in mapping number words to nonverbal approximate number representations in the service of estimation. Based on this, we conclude that analogical mapping provides a key mechanism to acquiring both the logic of counting and its association to perceptual representations, like those provided by the approximate number system.