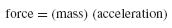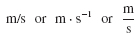Appendix A
Units
Problems in structural dynamics are based on Newton’s Second Law:
and these quantities, plus others directly related to them, must be expressed in a consistent system of units. At the present time, engineering practice is in the process of a conversion from English engineering units (United States Customary System) to the International System of Units (SI).[A.1] In English engineering units dimensional homogeneity is obtained in Eq. A.l when the force is given in lbf, the mass in slugs, and the acceleration in ft/sec2. This is the English ft-lbf-sec system of units. The slug is a derived unit, and from Eq. Al, 1 slug = 1 lbf-sec2/ft.
The units of force and mass frequently lead to confusion because of the use of the term weight as a quantity to mean either force or mass. On the one hand, when one speaks of an object’s “weight,” it is usually the mass, that is, the quantity of matter, that is referred to. On the other hand, in scientific and technological usage the term weight of a body has usually meant the force that if applied to the body would give it an acceleration equal to the local acceleration of free fall. This is the “weight” that would be measured by a spring scale. If the “mass” of a body is given in pounds (lbm), it must be divided by the acceleration of gravity g ≈ 32.2 ft/sec2 to obtain the mass as referred to in Newton’s Second Law, that is, a force of 1 lbf is exerted on a mass of 1 lbm by the gravitational pull of the Earth.
In structural dynamics and vibrations the in.-lbf-sec system is frequently used. In this system g = (32.2 ft/sec2) (12 in./ft) = 386 in./sec2 is used.
The International System of Units (SI) is a modern version of the metric system.[A.1] It is a coherent system1 with seven base units, for which names, symbols, and precise definitions have been established. Many derived units are defined in terms of the base units (Table A.1). Symbols have been assigned to each, and in some cases, they have been given names. In addition, there are supplementary units.
Table A.1 Some Derived SI Units and Supplementary SI Units

The base units are regarded as dimensionally independent. The ones of interest in structural dynamics are the meter (m), kilogram (kg),2 and second (s). One great advantage of SI is that there is one and only one unit for each physical quantity: the meter for length, the kilogram for mass, the second for time, and so on.
The unit of length, the meter, “is the length equal to 1 650 763.73 wavelengths in vacuum of the radiation corresponding to the transition between levels 2p10 and 5d5 of the krypton-86 atom. The kilogram is the unit of mass; it is equal to the mass of the international prototype of the kilogram.”[A.1] This prototype kilogram is preserved by the International Bureau of Weights and Measures near Paris, France. The second is the unit of time. It “is the duration of 9 192 631 770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the cesium-133 atom.”[A.1]
Reference A.l gives extensive tables of conversion factors and a number of rules to be followed in writing numbers and their units in correct SI form, Table A.2 gives the prefixes for the multiples and submultiples of SI units, and Table A.3 provides conversion factors for conversion from English units to SI units.
Table A.2 Prefixes for Multiples and Submultiples of SI Units
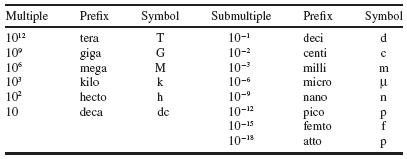
Table A.3 Examples of Conversionsa from English Units to SI Units
| To convert from: | To: | Multiply by: |
| foot (ft) | meter (m) | 3.048 000 E−01 |
| horsepower (550 ft-lbf/sec) | watt (W) | 7.456 999 E+02 |
| inch (in.) | meter (m) | 2.540 000 E−02 |
| kip (1000 lbf) | newton (N) | 4.448 222 E+03 |
| pound-force (lbf) | newton (N) | 4.448 222 E+00 |
| pound-force-inch (lbf-in.) | newton meter (N·m) | 1.129 848 E−01 |
| pound-force/inch (lbf /in.) | newton per meter (N/m) | 1.751 268 E+02 |
| pound-force/inch2 (psi) | pascal (Pa) | 6.894 757 E+03 |
| pound-mass (lbm) | kilogram (kg) | 4.535 924 E−01 |
| pound-mass/inch3 (lbm/in3) | kilogram per meter3 (kg/m3) | 2.767 990 E+04 |
| slug | kilogram (kg) | 1.459 390 E+01 |
aConversions should be handled with careful regard to the implied correspondence between the accuracy of the data and the number of digits.
A number of recommendations have been made in order to standardize the writing of numbers, symbols, and so on, in SI.[A.1] The following recommendations apply to situations encountered frequently.
a. When expressing a quantity by a numerical value and a unit, prefixes should preferably be chosen so that the numerical value lies between 0.1 and 1000.
b. Normally, the prefix should be attached to a unit in the numerator. One exception to this is when the kilogram is one of the units.
c. No space is used between the prefix and the unit symbol.
a. Unit symbols should be printed in roman (upright) type regardless of the type style used in the surrounding text.
b. Unit symbols are not followed by a period except when used at the end of a sentence.
c. In the complete expression for a quantity, a space should be left between the numerical value and the unit symbol.
A.3 UNITS FORMED BY MULTIPLICATION AND DIVISION
With unit names:
a. Product. Use a space (newton meter) or a hyphen (newton-meter).
b. Quotient. Use the word per and not the solidus (/).
c. Powers. Use the modifier squared or cubed placed after the unit name (meter per second squared).
With unit symbols:
a. Product. Use a centered dot (Nm).
b. Quotient. Use one of the following forms:
Outside the United States the comma is sometimes used as a decimal marker. To avoid this potential source of confusion, recommended international practice calls for separating the digits into groups of three, counting from the decimal point toward the left and the right, and using a small space to separate the groups.
REFERENCE
[A.1] An American National Standard, ASTM/IEEE, Standard Metric Practice, ASTM E 380-76, IEEE Std. 268-1976, ANSI Z210.1-1976, Institute of Electrical and Electronics Engineers, New York, 1976.
1A coherent system of units is one in which there are no numerical factors that must enter into an equation employing numerical values; for example, Eq. A.1 is valid whether it is written in symbols or in numerical values—there is an implied multiplicative factor of 1 on the right-hand side.
2In SI units the kilogram is a unit of mass. The kilogram-force (from which the suffix “force” is often omitted) should not be used.