Back to Kernel trick

So, now we have got a fair understanding of kernel and its importance. And, as discussed in the last section, the kernel function is:

K(x_i,x_j)= x_i . x_j

So, now the margin problem becomes the following:

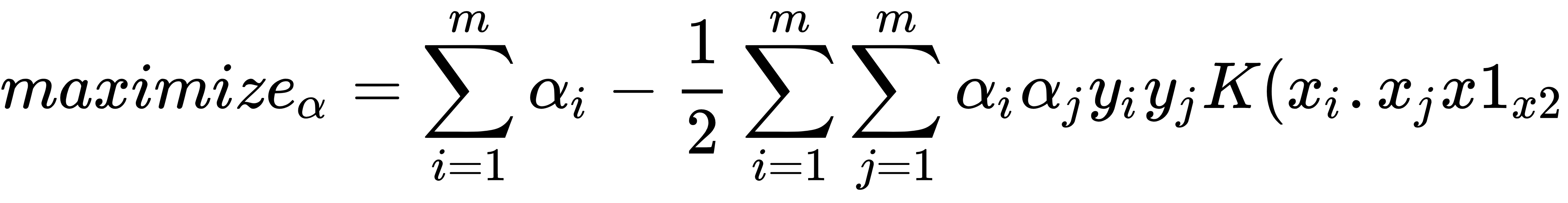
This is subject to 0 ≤ α_i ≤ C, for any i = 1, ..., m:

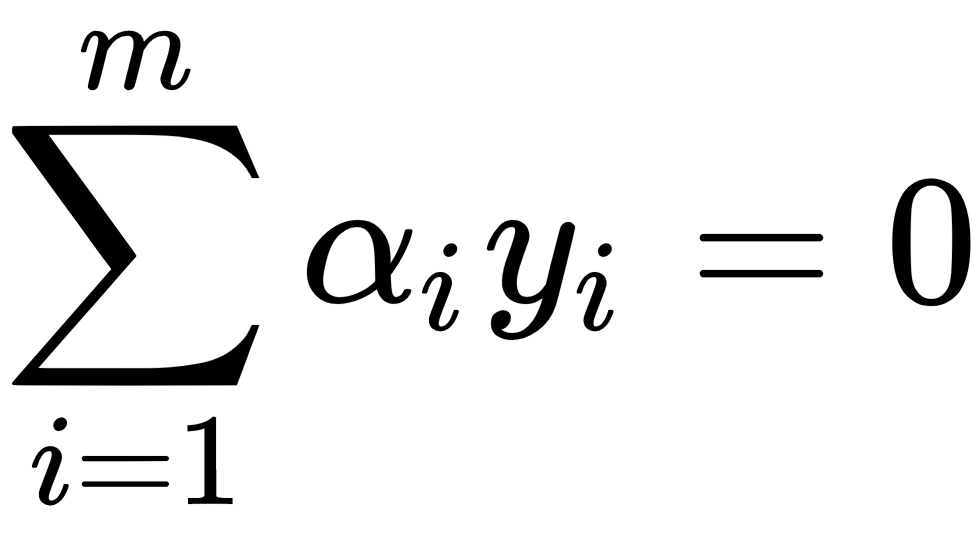
Applying the kernel trick simply means replacing the dot product of two examples with a kernel function.

Now even the hypothesis function will change as well:

This function will be able to decide on and classify the categories. Also, since S denotes the set of support vectors, it implies that we need to compute the kernel function only on support vectors.