Neural networks have been a revelation in extracting complex features out of the data. Be it images or texts, they are able to find the combinations that result in better predictions. The deeper the network, the higher the chances of picking those complex features. If we keep on adding more hidden layers, the learning speed of the added hidden layers get faster.
However, when we get down to backpropagation, which is moving backwards in the network to find out gradients of the loss with respect to weights, the gradient tends to get smaller and smaller as we head towards the first layer. It that initial layers of the deep network become slower learners and later layers tend to learn faster. This is called the vanishing gradient problem.
Initial layers in the network are important because they are responsible to learn and detect the simple patterns and are actually the building blocks of our network. Obviously, if they give improper and inaccurate results, then how can we expect the next layers and the complete network to perform effectively and produce accurate results? The following diagram shows the figure of a ball that rolls on a steeper slope:
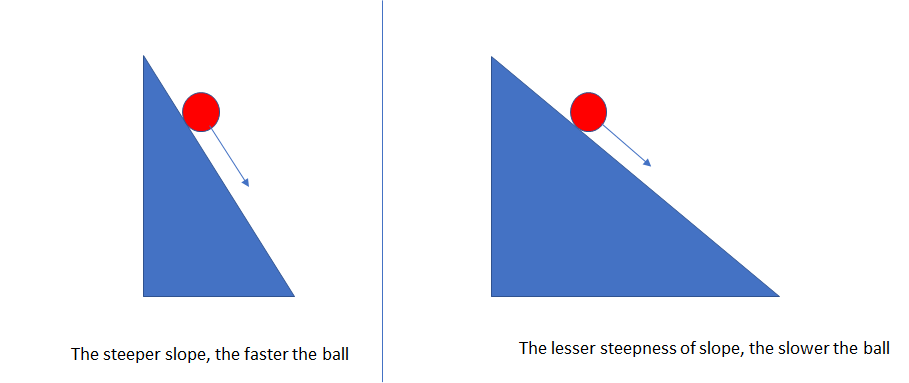
Just to make it a little simpler for us all, let's say that there are two slopes: one being steeper and the other being less steep. Both slopes have got balls rolling down them and it is a no brainer that the ball will roll down the steeper slope faster than the one that is not as steep. Similar to that, if the gradient is large, the learning and training gets faster; otherwise, training gets too slow if the gradient is less steep.
From backpropagation intuition, we are aware of the fact that the optimization algorithms such as gradient descent slowly seeko attain the local optima by regulating weights such that the cost function's output is decreased. The gradient descent algorithm updates the weights by the negative of the gradient multiplied by the learning rate (α) (which is small):

It says that we have to repeat until it attains convergence. However, there are two scenarios here. The first is that, if there are fewer iterations, then the accuracy of the result will take a hit; the second is that more iterations result in training taking too much time. This happens because weight does not change enough at each iteration as the gradient is small (and we know α is already very small). Hence, weight does not move to the lowest point in the assigned iterations.
Let's talk about that activation function, which might have an impact on the vanishing gradient problem. Here, we talk about the sigmoid function, which is typically used as an activation function:


It translates all input values into a range of values between (0,1). If we have to find out the derivative of the sigmoid function then:

Let's plot it now:

It is quite evident that the derivative has got the maximum value as 0.25. Hence, the range of values under which it would lie is (0,1/4).
A typical neural network looks like the following diagram:

Once the weight parameters are initialized, the input gets multiplied by weights and gets passed on through an activation function and, finally, we get a cost function (J). Subsequently, backpropagation takes place to modify the weights through gradient descent in order to minimize J.
In order to calculate the derivative with respect to first weight, we are using the chain rule. It will turn out to be like the following:

If we just try to study the derivatives in the middle of the preceding expression, we get the following:

Part 1—from the output to hidden2.
Since the output is the activation of the 2nd hidden unit, the expression turns out to be like the following:


Similarly for part 2, from hidden 2 to hidden 1, the expression turns out to be like the following:


On putting everything together, we get the following:

We know that the maximum value of the derivative of the sigmoid function is 1/4 and the weights can typically take the values between -1 and 1 if weights have been initialized with standard deviation 1 and mean 0. It will lead to the whole expression being smaller. If there is a deep network to be trained, then this expression will keep on getting even smaller and, as a result of that, the training time will become slow-paced.