Random walk is a time series model where the current observation is equal to the previous observations with a random modification. It can be described in the following manner:
xt= xt-1 + wt
In the preceding formula, wt is a white noise series.
Sometimes, we might come across a series that reflects irregular growth. In these cases, the strategy to predict the next level won't be the correct one. Rather, it might be better to try to predict the change that occurs from one period to the next—that is, it may be better to look at the first difference of the series in order to find out a significant pattern. The following figure shows a random walk pattern:
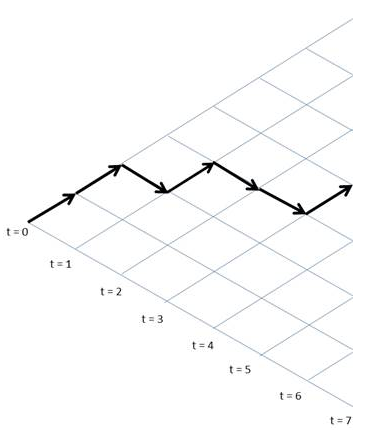
In each time period, going from left to right, the value of the variable takes an independent random step up or down, which is called a random walk.
It can also be described in the following way:
y(t)= bo + b1*xt-1 + wt
The following list explains the preceding formula:
- y(t): Next value in the series
- bo: Coefficient, which, if set to a number other than zero, means that the random walk comes along with a drift
- b1: Coefficient, which is set to 1
- wt: White noise