In the previous chapter, we understood what principal component analysis (PCA) is, how it works, and when we should be deploying it. However, as a dimensionality reduction technique, do you think that you can put this to use in every scenario? Can you recall the roadblock or the underlying assumption behind it that we discussed?
Yes, the most important assumption behind PCA is that it works for datasets that are linearly separable. However, in the real world, you don't get this kind of dataset very often. We need a method to capture non-linear data patterns.
On the left-hand side, we have got a dataset in which there are two classes. We can see that once we arrive at the projections and establish the components, PCA doesn't have an effect on it and that it is not able to separate it by a line in a 2D dimension. That is, PCA can only function well when we have got low-level dimensions and linearly separable data. The following plot shows the dataset of two classes:
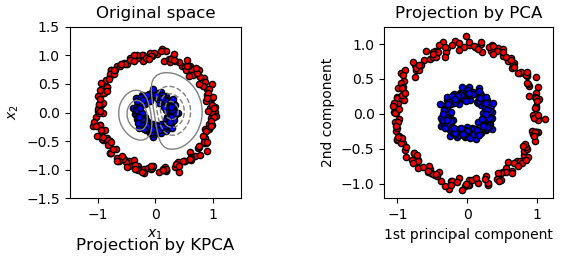
This is why we bring in the kernel method: so that we can merge it with PCA to achieve it.
Just to recap what you learned about the kernel method, we will discuss it and its importance in brief:
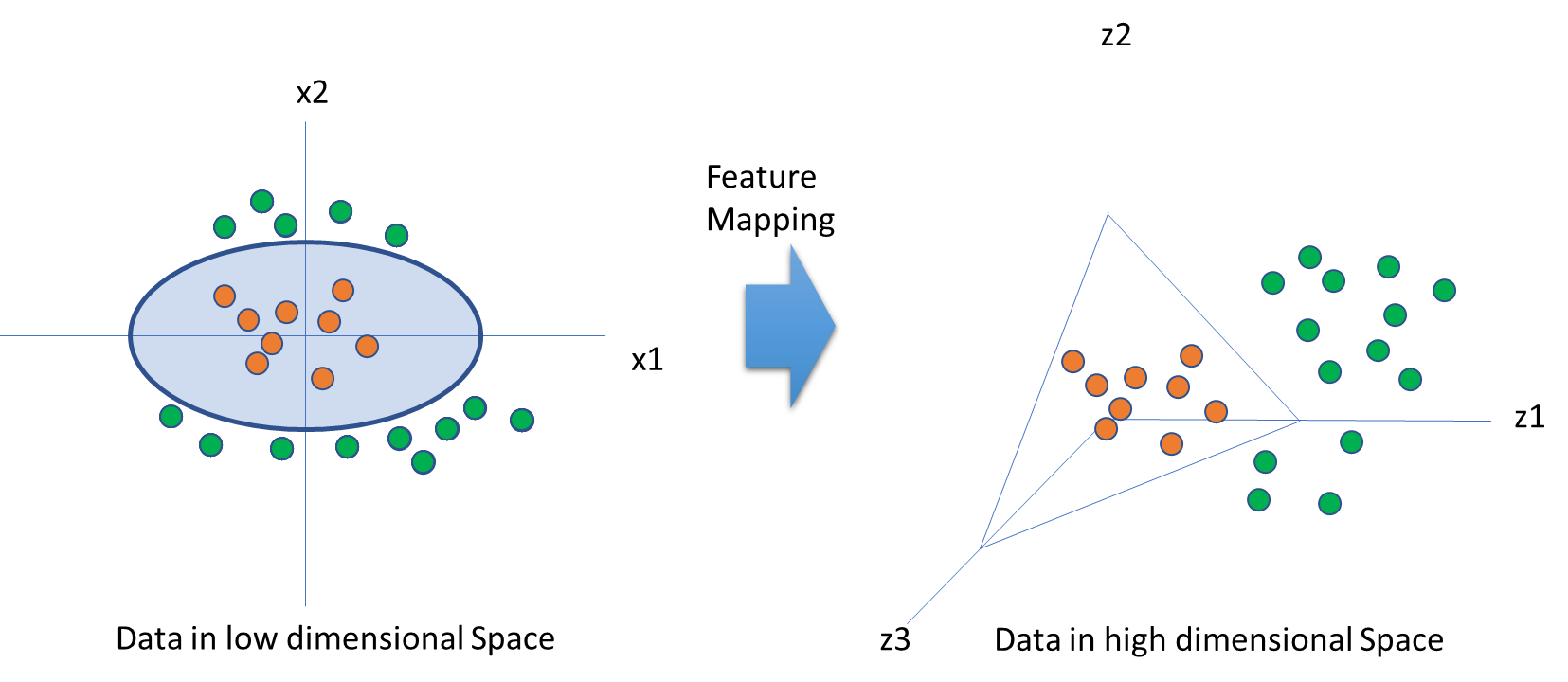
- We have got data in a low dimensional space. However, at times, it's difficult to achieve classification (green and red) when we have got non-linear data (as shown in the following diagram). This being said, we do have a clear understanding that having a tool that can map the data from a lower to a higher dimension will result in a proper classification. This tool is called the kernel method.
- The same dataset turns out to be linearly separable in the new feature space.
The following diagram shows data in low and high dimensional spaces:
To classify the green and red points in the preceding diagram, the feature mapping function has to take the data and change is from being 2D to 3D, that is, Φ = R2 → R3. The equation for this is as follows:
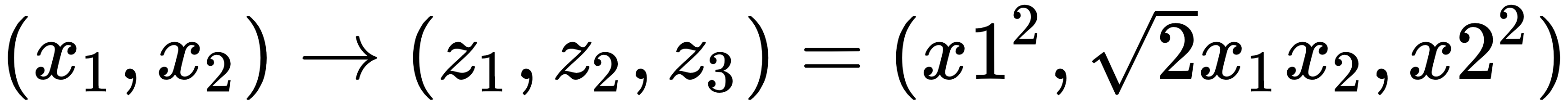
The goal of the kernel method is to figure out and choose kernel function K. This is so that we can find the geometry feature in the new dimension and classify data patterns. Let's see how this is done:

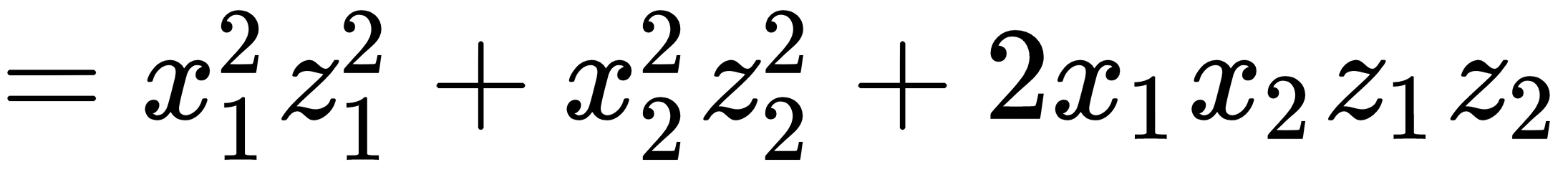
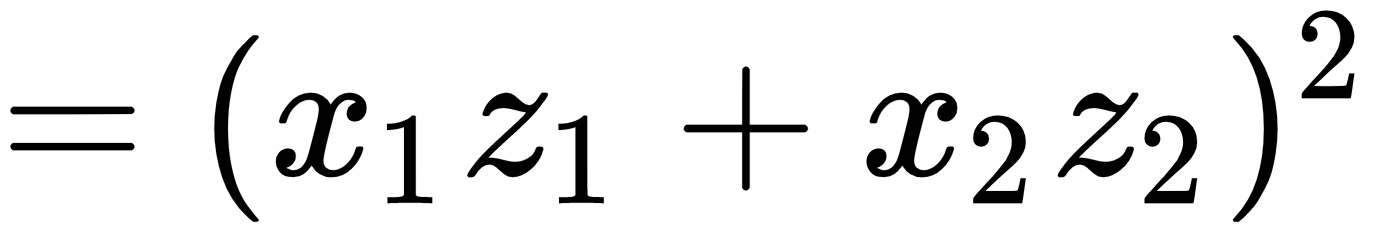


Here, Phi is a feature mapping function. But do we always need to know the feature mapping function? Not really. Kernel function K does the trick. With a given kernel function, K, we can come up with a feature space, H. Two of the popular kernel functions are Gaussian and polynomial kernel functions.
Picking an apt kernel function will enable us to figure out the characteristics of the data in the new feature space quite well.
Now that we have made ourselves familiar with the kernel trick, let's move on to the Kernel PCA.