Compressed sensing is one of the easiest problems to solve in the area of information theory and signal processing. It is a signal acquisition and reconstruction technique where the signal is compressible. The signal must be sparse. Compressed sensing tries to fit samples of a signal to functions, and it has a preference to use as few basic functions as possible to match the samples. This is described in the following diagram:
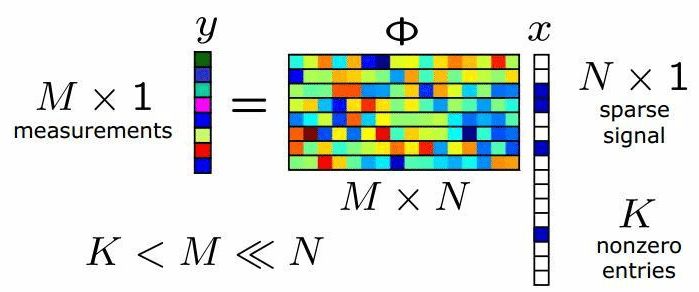
This is one of the prime equations that we see in linear algebra, where y is a M x 1 matrix, phi is a M x N matrix that has got a number of columns that is higher than the number of rows, and x is a N x 1 matrix comprising k non-zero entries. There are so many unknowns, which is expressed as an N length vector and M measurements, wherein M << N. In this type of equation, we know that many solutions are possible since the null space of this matrix is non-trivial. Hence, this equation can accommodate many solutions.