CPT

Let's do the CPT for connector 1:

	The dog barks	The dog doesn't bark	Aggregate
It rains	10	4	14
It doesn't rain	8	5	13
Aggregate	18	9	27

 

Here, we are talking about the following scenarios:

• Probability (Dog barks|It rains) = 10/14
• Probability (Dog doesn't bark | It rain) = 4/14
• Probability (Dog barks | It doesn't rain) = 8/13
• Probability (Dog doesn't bark | It doesn't rain) = 5/13

	The dog barks	The dog doesn't bark
It rains	10/14	4/14
It doesn't rain	8/13	5/13

 

The following diagram shows the probabilities in detail:

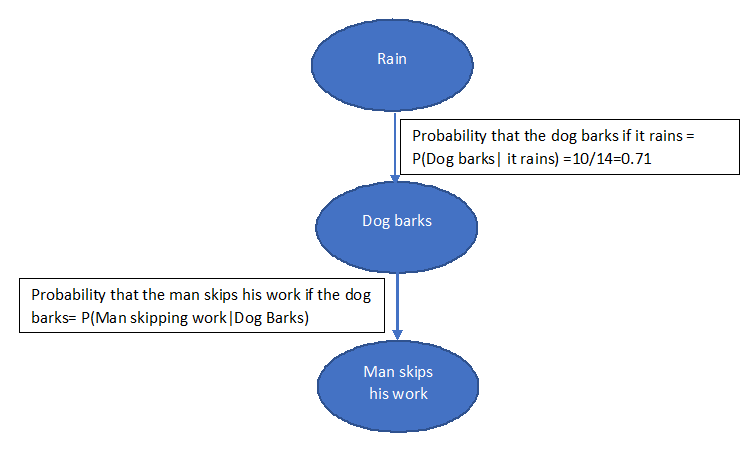
Let's say if the probability of rain = P(rain) =0.6 then the probability of no rain = P(no rain) = 0.4.

Let's say that the CPT for the man skipping work is as follows:

	The man skips work	The man doesn't skip work
The dog barks	0.8	0.2
The dog doesn't bark	0.3	0.7

The probability of every event has to be calculated with respect to the parent node.

And now, we are supposed to find out the probability of the man skipping work and the dog barks but it doesn't rain = P (Man skips work, the dog barks, it doesn't rain):

= P (Man skips work|the dog barks) *P (the dog barks|it doesn't rain) *P(it doesn't rain)

=0.8 * (8/13) *0.4

=0.1969