Gaussian kernel

The polynomial kernel has given us a good boundary line. But can we work with polynomial kernels all the time? Not in the following scenario:

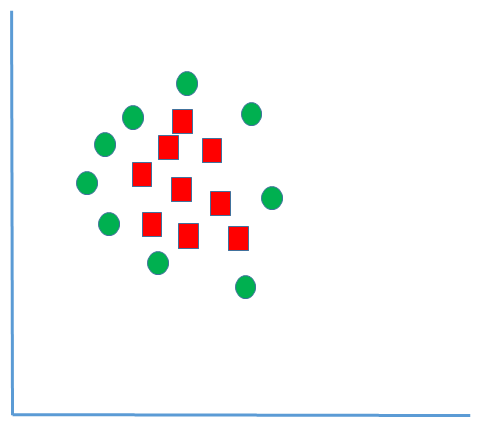
The solution is a radial basis function or Gaussian kernel. It's nothing but the similarity function of the vectors to translate them into a high dimensional space or infinite dimensional space. Its value depends on the distance from the Gaussian kernel function, as follows:

K(x,x^') = exp(-γ ||x-x'||²)

 

Without loss of generality, let :

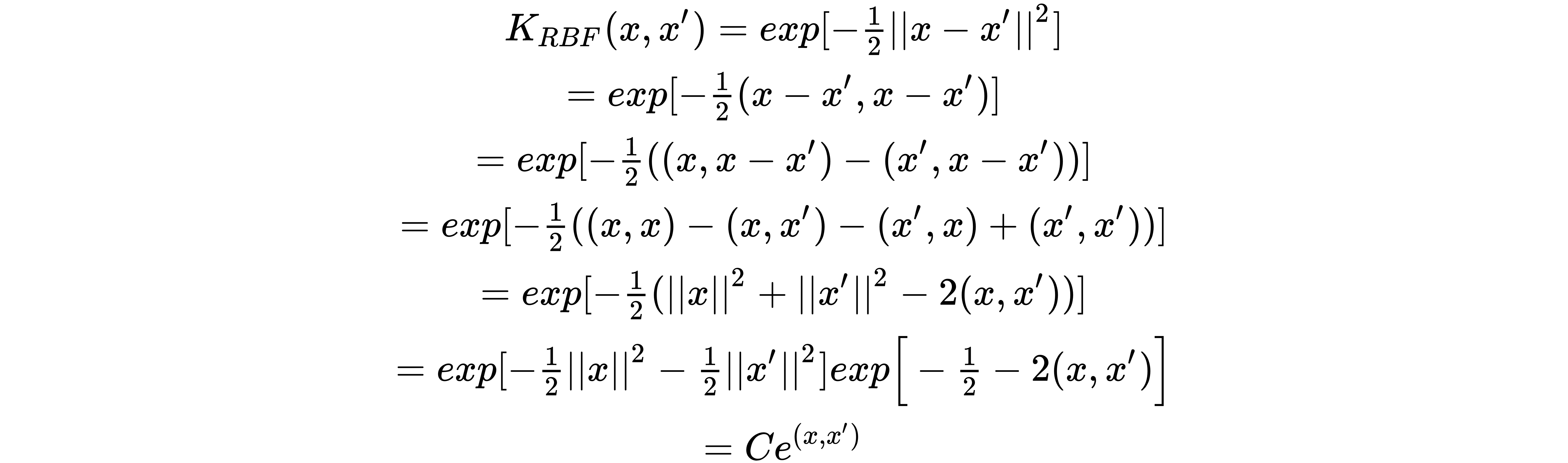
With the help of this RBF as a similarity function, all the feature vectors get calculated.