To explain gradient boosting, we will take the route of Ben Gorman, a great data scientist. He has been able to explain it in a mathematical yet simple way. Let's say that we have got nine training examples wherein we are required to predict the age of a person based on three features, such as whether they like gardening, playing video games, or surfing the internet. The data for this is as follows:

To build this model, the objective is to minimize the mean squared error.
Now, we will build the model with a regression tree. To start with, if we want to have at least three samples at the training nodes, the first split of the tree might look like this:

This seems to be fine, but it's not including information such as whether they play video games or browse the internet. What if we plan to have two samples at the training nodes?
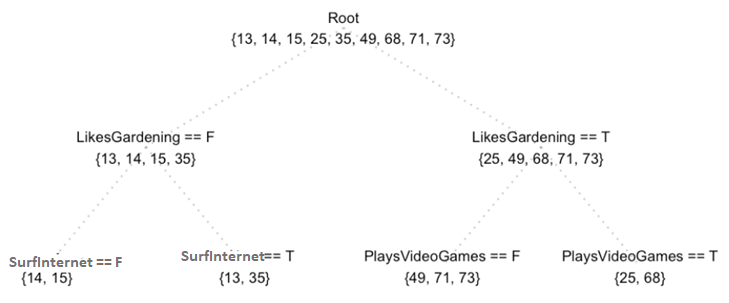
Through the preceding tree, we are able to get certain information from features, such as SurfInternet and PlaysVideoGames. Let's figure out how residuals/errors come along:

Now, we will work on the residuals of the first model:

Once we have built the model on residuals, we have to combine the previous model with the current one, as shown in the following table:

We can see that the residuals have come down and that the model is getting better.
Let's try to formulate what we have done up until this point:
- First, we built a model on the data f1(x) = y.
- The next thing we did was calculate the residuals and build the model on residuals:
h 1(x)=y- f1(x)
- The next step is to combine the model, that is, f2(x)= f1(x) + h 1(x).
Adding more models can correct the errors of the previous models. The preceding equation will turn out to be as follows:
f3(x)= f2(x) + h2(x)
The equation will finally look as follows:
fm(x)= fm-1(x) + hm-1(x)
Alternatively, we can write the following:
hm(x)= y- fm(x)
- Since our task is to minimize the squared error, f will be initialized with the mean of the training target values:

- Then, we can find out fm+1, just like before:
fm(x)= fm-1(x) + hm-1(x)
Now, we can use gradient descent for our gradient boosting model. The objective function we want to minimize is L. Our starting point is fo(x). For iteration m=1, we compute the gradient of L with respect to fo(x). Then, we fit a weak learner to the gradient components. In the case of a regression tree, leaf nodes produce an average gradient among samples with similar features. For each leaf, we step in the direction of the average gradient. The result is f1 and this can be repeated until we have fm.
We modified our gradient boosting algorithm so that it works with any differentiable loss function. Let's clean up the preceding ideas and reformulate our gradient boosting model once again.