We will study the different frequent pattern tree growth from the following rows:
- Row 1: Every FP-Tree starts with a null node as a root node. Let's draw the first row of the tree order along with their frequency:
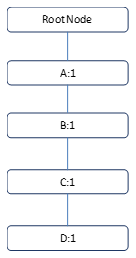
- Row 2: It has got {B,C,D}. A is missing, so we can not merge it with the earlier node. Hence, we will have to create another node, altogether as shown here:

- Row 3: It has got {A,D}. B and C are missing, but we can tie it with the earlier node. A encounters a repetition, so frequency will change. It becomes 2 now:

- Row 4: It has got {A,B}. We can tie it with the earlier node and will traverse on the previous node. A and B encounters a repetition, so frequency will change for it. It becomes 3 and 2 respectively:

- Row 5: It has got {A,B,C}. Again, it can be tied with the earlier node and A, B, and C see a repetition, so the frequency will change for them. It becomes 4, 3, and 2 respectively:
