Polynomial kernel

If there are two vectors, x₁ and x₂, the linear kernel can be defined by the following:

K(x_1, x₂)= (x_{1 .} x₂ + c)^d

Where:

• c: Constant
• d: Degree of polynomial:

def polynomial_kernel(x1, x2, degree, constant=0): 
    result = sum([x1[i] * x2[i] for i in range(len(x1))]) + constant 
    return pow(result, degree)

If we use the same x1 and x2 as used previously, we get the following:

x1= [4,8]
x2=[20,30] 
polynomial_kernel(x1,x2,2,0)
# result would be 102400

If we increase the degree of polynomial, we will try to get influenced by other vectors as the decision boundary becomes too complex and it will result in overfitting:

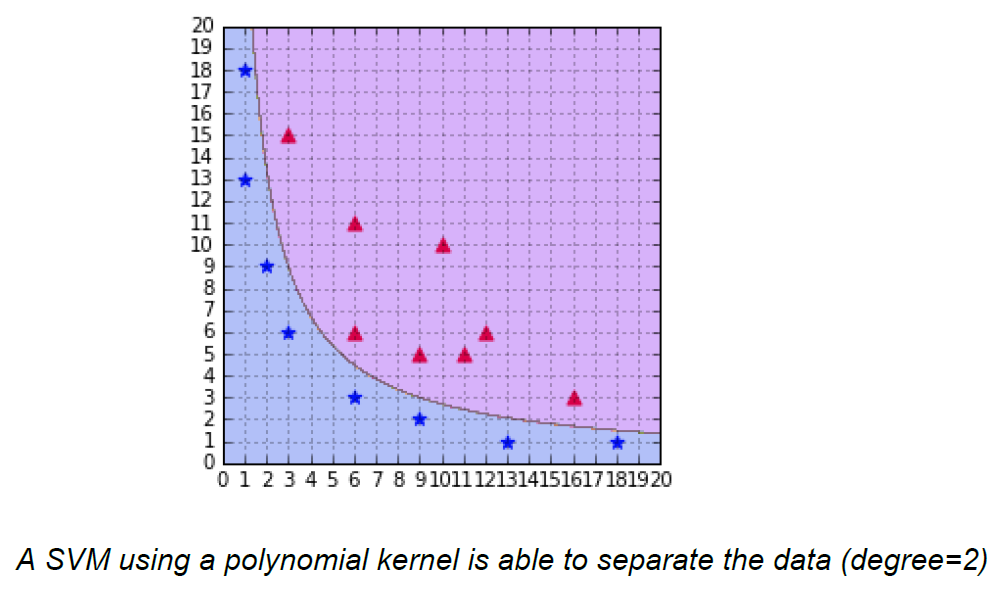
Polynomial kernel using degree as 6.