Runge-Kutta is a set of numerical methods for approximating the solutions of differential equations. A differential equation is an equation that consists of the derivative of a variable (think the rate of change) defined in terms of another, independent variable (think physical property). For example, consider a virus. As a virus spreads, its rate of infection becomes faster and faster. The same is true for population growth in most species. Most often used in such fields as biology, engineering, physics, and economics, differential equations are extremely handy for expressing complex systems. Unfortunately, only the most trivial of differential equations can be explicitly solved. For the rest, we use numerical methods such as Runge-Kutta, which was developed by mathematicians Carl Runge and Wilhelm Kutta.
While Runge-Kutta is technically a set of numerical methods, the fourth-order Runge-Kutta method is the most widely used and is often abbreviated RK4. Runge-Kutta essentially attempts to find the next point on a line. The next point on the line is expressed in terms of a function of two variables, such as the independent variable time and some other dependent value.
Formally, the Runge-Kutta is expressed in terms of the initial conditions:

The variable y is an unknown function of time. However, we know that the rate at which y changes is a function of time (t) and y itself. The rate of change is the first derivative. The Runge-Kutta methods specify that we choose a step size for time, defined as the variable h. All this means is that we have chosen how far in the future we wish to calculate the next value of the variable y. We can now define the following two equations as the values for our next value of time and our next value of y:

The values for k1, k2, k3, and k4 are defined as follows:
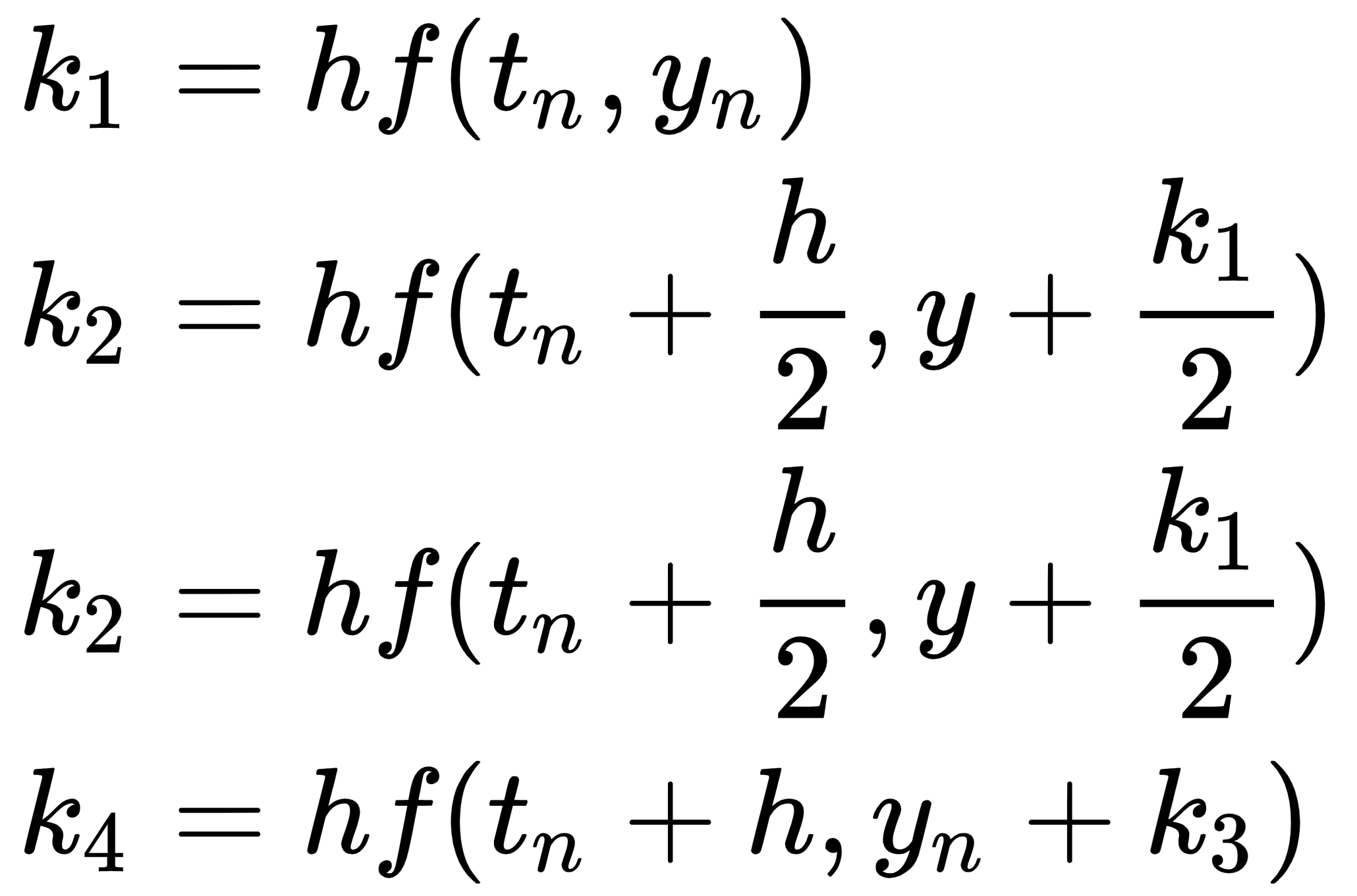
That's a lot of math. What's more, we can pick a step size, h, that is smaller than the actual next point in time that we are interested in. When we do this, we can compute the preceding formulas iteratively until we arrive at the point in time of interest. In other words, if we begin at time (t) = 0 and are interested in t = 2 seconds, we could define h as .5 seconds. We would then compute the calculations for Runge-Kutta four times, with the value for k4 from each iterative step feeding into the next computation of k1 as yn.
If this all makes your brain hurt, never fear; this recipe demonstrates an implementation for multiple iterations of RK4 in DAX. Runge-Kutta was specifically chosen because of its iterative (recursive) behavior. Thus, this recipe demonstrates a method of simulating recursion within DAX. For an alternative method of simulating recursion, see the Simulating recursion recipe in Chapter 10, Using Uncommon DAX Patterns.