The hypergeometric distribution is a probability distribution that defines the probability of having a specified amount of success (k) within a specified number of attempts (n) for a given population of N with K items with the desired feature. So, if we consider a deck of cards, what is the probability of drawing 2 (k) jacks within 10 (n) draws from a deck of 52 (N) cards in which there are 4 (K) jacks? The formula for the hypergeometric distribution formula is as follows:
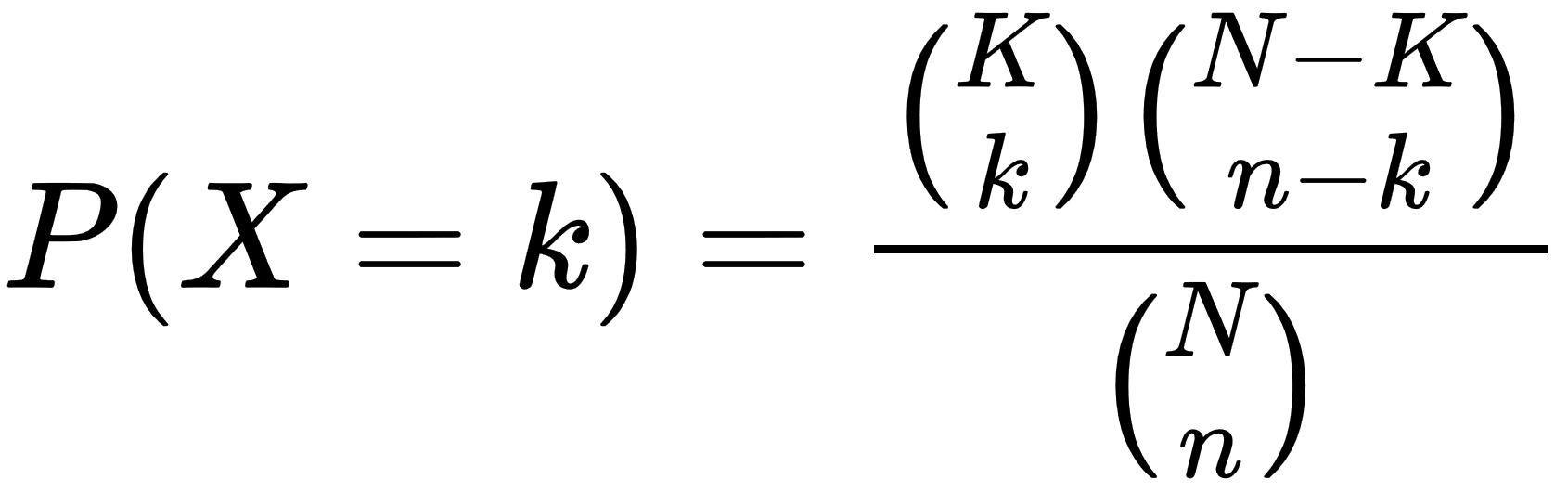
Those odd-looking things in parenthesis are binomial distributions (combinations).
Not only constrained to gambling, the hypergeometric distribution has a wide range of uses and can be used to determine the statistical significance of specific events (successes). Thus, we can use the hypergeometric distribution to determine under- or over-representation of a sub-population within a given population sample. In other words, businesses could use the hypergeometric distribution formula to determine the characteristics of their customer base.
This recipe demonstrates how to implement the formula for hypergeometric distribution in DAX.