The Mann-Kendall test requires a number of elements to be calculated or set, including alpha, n, S, freq, se, z-stat, and p-value. Each of these elements is a measure within our recipe, and each is explained in turn here.
The first measure, alpha, is the significance level. In statistics, this generally defaults to 0.05, so we simply set our alpha variable to .05.
The second measure, n, is simply the count of the number of observations, or rows in our data table, R05_Table. We simply use COUNTROWS to compute this value.
The next element, measure S, is much more tricky to calculate. The formula for S is as follows:

To implement this formula in DAX, we first have to understand what the formula for S is trying to accomplish. Essentially, what is going on here is that every value in the series is compared with every preceding value and we record a -1 if the preceding value is larger and a 1 if the preceding value is smaller. Ties are 0. The idea is that if there is a trend present, the sign values will tend to either be constantly negative or constantly positive. A negative value of S indicates that values tend to be lower, and a positive value for S indicates that values tend to be higher.
The implementation of this in DAX starts by creating the table variable, __Table. __Table begins with our base table, R05_Table, and then adding the __S column using ADDCOLUMNS. The calculation of the __S column uses nested variables. We start by simply recording the current value of the row, __Value. We then construct the nested table variable, __Table. We can reuse the variable name __Table here because we are nesting variables. The nested variable, __Table, uses FILTER to select only the rows where the ID column is less than the current ID column (EARLIER). We can now use COUNTX to count how many previous rows have a Value column that is less than our current row's Value column, __Value. This count is stored in the __Pos variable. We then compute the __Neg variable in the same manner as the __Pos variable except that we count how many previous values are greater than our current value. Finally, we simply RETURN the difference between __Pos and __Neg. The final step for computing S is to simply sum our __S column in __Table using SUMX.
From the sign of S, we now know whether our values tend to be larger or smaller over time. Our next task is to determine if this tendency is significant. The first step in this process is to account for ties. This is the purpose of the freq measure. To compute the freq measure, we start by creating the table variable, __Table, using GROUPBY to group our data by the Value column and add the __Count column. The __Count column uses COUNTX to count the number if ID values in the CURRENTGROUP. We then use ADDCOLUMNS to add the __Ties column, which is simply our __Count minus 1. Next, we use ADDCOLUMNS again to add the __Freq column. If the __Ties column is 0, then the value of our __Freq column is also set to 0. Otherwise, our __Freq column is set to __Ties multiplied by __Ties plus 1, multiplied by 2 times __Ties plus 7. We can now create the __Sum variable by simply using SUMX to sum our __Freq column within __Table. Finally, we make certain that __Sum is not blank (ISBLANK) and either return 0 if __Sum is blank or __Sum if it's not blank.
The next step is to compute se. se is the square root of our variance, and our variance is given by the following formula:
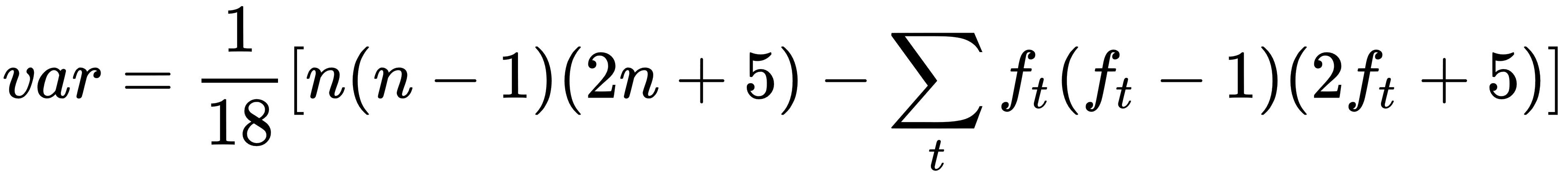
As we have seen, n is simply the number of observations or values in our data. The summation part of the formula is simply our frequency summed over time t. We have already computed our frequency as the freq measure. Thus, our calculation for se is relatively straightforward, and we simply implement the formula for the variance, substituting our freq measure for the summation portion of the formula and calculate the square root using the SQRT function.
The z-stat measure is next. z-stat is based on the following formula:
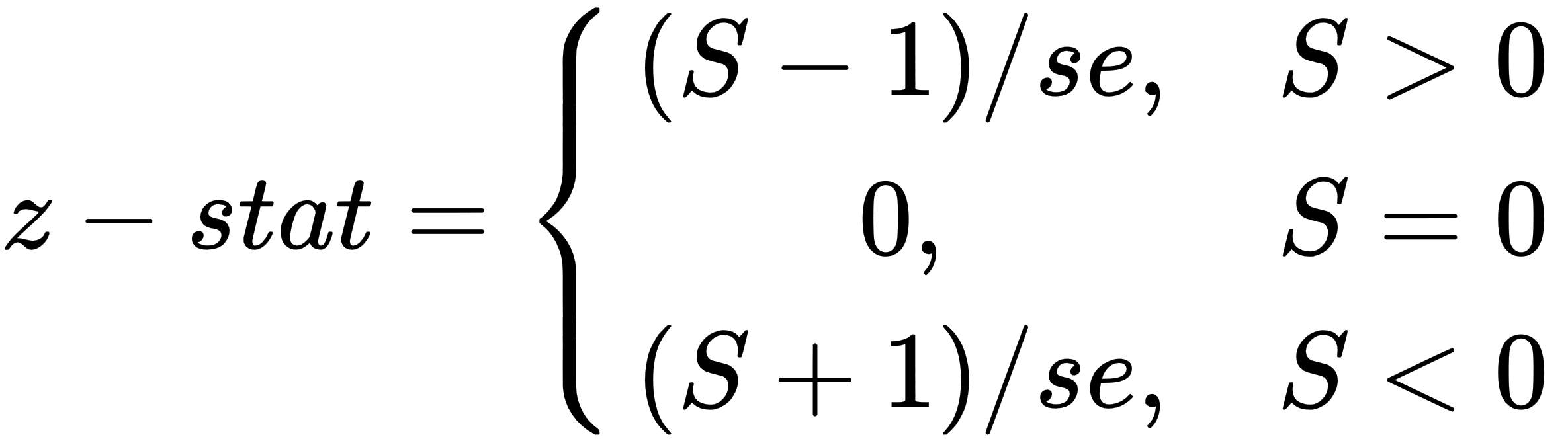
We can easily implement this logic using a SWITCH statement, with its first parameter being the TRUE function.
We can now calculate our p-value measure by finding the normal distribution of the negative absolute value of our z-stat measure using the NORM.S.DIST function.
Finally, we can compare our p-value measure to our alpha measure to determine if the trend is significant. This is the trend measure. If our p-value measure is less than our alpha measure, then the trend is significant and we return Yes. Otherwise, we return No.