2
If nature were not beautiful it would not be worth knowing, and if nature were not worth knowing, life would not be worth living.
—Henri Poincaré
I WASTED A LOT OF TIME at university playing billiards in our student common room. I could have pretended that it was all part of my research into angles and stuff, but the truth is that I was procrastinating. It was a good way of putting off having to cope with not being able to answer that week’s set of problems. But, in fact, the billiard table hides a lot of interesting mathematics in its contours, mathematics highly relevant to my desire to understand my dice.
If I shoot a ball around a billiard table and mark its path, then follow that by shooting another ball off in very nearly the same direction, the second ball will trace out a path very similar to the first ball. Poincaré had conjectured that the same principle applied to the solar system. Fire a planet off in a slightly different direction and the solar system will evolve in a very similar pattern. This is most people’s intuition—if I make a small change in the initial conditions of the planet’s trajectory it won’t alter the course of the planet much. But the solar system seems to be playing a slightly more interesting game of billiards than the ones I played as a student.
Rather surprisingly, if you change the shape of the billiard table this intuition turns out to be wrong. If you shoot balls around a billiard table shaped like a stadium with semicircular ends but straight sides, the paths can diverge dramatically even if the balls started off heading in almost exactly the same direction. This is the signature of chaos theory: sensitivity to very small changes in the initial conditions.
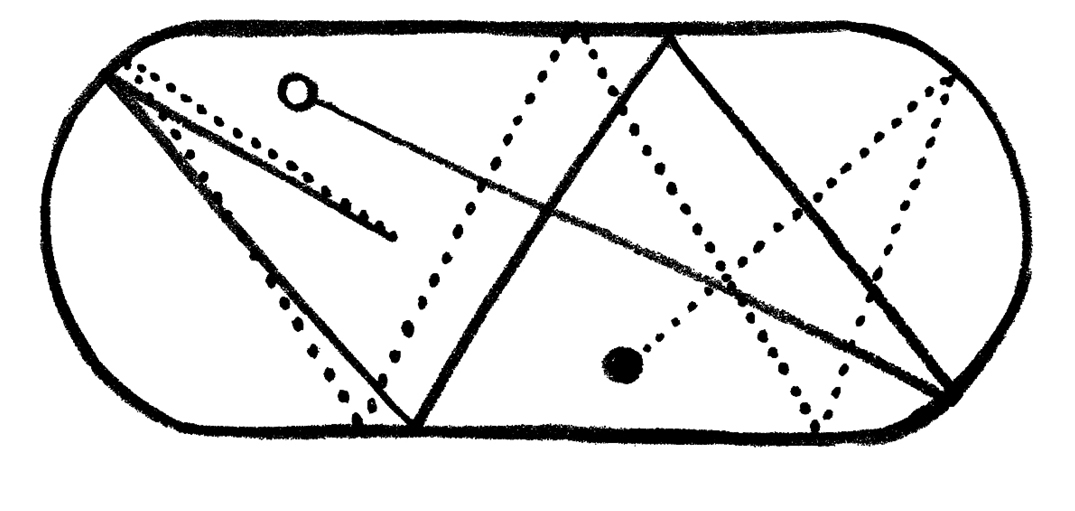
Two quickly diverging paths taken by a billiard ball around a stadium-shaped billiard table
So the challenge is to determine whether the fall of my dice can be predictable, like a conventional game of billiards, or whether we are playing a giant game of chaotic billiards.
Poincaré is generally credited as the father of chaos theory, but the sensitivity of dynamic systems to small changes was not very well known for decades into the twentieth century. It really took the rediscovery of the phenomenon by scientist Edward Lorenz, who like Poincaré thought he’d made some mistake, before the ideas of chaos theory became more widely known.
While working as a meteorologist at the Massachusetts Institute of Technology in 1963, Lorenz had been running equations for the change of temperature in a dynamic fluid on his computer when he decided he needed to rerun one of his models for longer. So he took some of the data that had been output earlier in the run and re-entered it, expecting to be able to restart the model from that point.
When he returned from coffee, he discovered to his dismay that the computer hadn’t reproduced the previous data and that it had very quickly generated a wildly divergent prediction. At first he couldn’t understand what was happening. If you input exactly the same numbers into an equation, you don’t expect to get a different answer at the other end. It took him a while to realize what was going on: he hadn’t input the same numbers. The computer printout of the data he’d used had only printed the numbers to three decimal places, while it had been calculating using the numbers to six decimal places.
Even though the numbers were different, they differed only in the fourth decimal place. You wouldn’t expect this to make that big a difference, but Lorenz was struck by the impact of such a small difference on the resulting data. Here are two graphs created using the same equation, where the data that are put into the equations differ very slightly. One graph uses the input data 0.506127 and the second graph approximates this to 0.506. Although the graphs start out following similar paths, they very quickly behave completely differently.

The model that Lorenz was running was a simplification of weather models that analyzed how the flow of air behaves when subjected to differences in temperature. His rediscovery of how small changes in starting conditions can have such a big impact on future outcomes would have huge implications for our attempts to use mathematical equations to predict the future. As Lorenz wrote, “Two states that were imperceptibly different could evolve into two considerably different states. Any error in the observation of the present state—and in a real system, this appears to be inevitable—may render an acceptable prediction of the state in the distant future impossible.”
When Lorenz sought to explain his findings to a colleague, he was told, “Edward, if your theory is correct, one flap of a seagull’s wings could alter the course of history forever.” The seagull would eventually be replaced by the now famous butterfly when Lorenz presented his findings in 1972 at the American Association for the Advancement of Science in a paper titled “Does the Flap of a Butterfly’s Wings in Brazil Set off a Tornado in Texas?”
Curiously, both the seagull and the butterfly might have been preempted by the grasshopper. It seems that already in 1898 Professor W. S. Franklin had realized the devastating effect that the insect community could have on the weather. In a book review, he posited, “An infinitesimal cause may produce a finite effect. Long-range detailed weather prediction is therefore impossible, and the only detailed prediction which is possible is the inference of the ultimate trend and character of a storm from observations of its early stages; and the accuracy of this prediction is subject to the condition that the flight of a grasshopper in Montana may turn a storm aside from Philadelphia to New York!”
This is an extraordinary position to be in. Science offers a completely deterministic description of the evolution of many dynamic systems like the weather. And yet in many cases we are denied access to its predictions, as any measurement of the location or wind speed of a particle is inevitably going to be an approximation of its true conditions.
The National Weather Service, when making weather predictions, takes the data recorded by weather stations dotted across a region and then, instead of running equations on these data, the meteorologists do several thousand runs, varying the data over a range of values. The predictions stay close for a while, but by about five days into the future the results have often diverged so wildly that one set of data predicts a heat wave while a few changes in the decimal places of the data result in drenching rain.
“There is a maxim which is often quoted, that ‘The same causes will always produce the same effects,’” wrote the great Scottish scientist James Clerk Maxwell in his book Matter and Motion, published in 1877. “There is another maxim which must not be confounded with this, which asserts that ‘Like causes produce like effects.’ This is only true when small variations in the initial circumstances produce only small variations in the final state of the system.” The discovery of chaos theory in the twentieth century revealed this maxim to be false.
Of course, there are times when small changes don’t alter the course of the equations dramatically, like the paths in the classic billiard table. So how can you know the point when you can’t know what is going to happen next? Robert May discovered a beautiful example when he analyzed the equations for population growth.
Born in Australia in 1938, May had originally trained as a physicist working on superconductivity, but his academic work took a dramatic turn when he was exposed in the late 1960s to the newly formed movement for social responsibility in science. His attention shifted from the behavior of collections of electrons to the more pressing questions of the behavior of population dynamics in animals. Biology, at the time, was not a natural environment for the mathematically minded, but following May’s work that would change. This fusion of the hardcore mathematical training he’d received as a physicist with a new interest in biology led to his great breakthrough.
In a paper in Nature called “Simple Mathematical Models with Very Complicated Dynamics,” published in 1976, May explored the dynamics of a mathematical equation describing population growth from one season to the next. He revealed how even a quite basic equation can produce extraordinarily complex results. His equation for population dynamics wasn’t some complicated differential equation but a simple, discrete feedback equation that anyone with a calculator could explore.
May's Feedback Equation for Population Dynamics
Consider a population of animals whose numbers can vary between 0 and some hypothetical maximum value that I will call N. Given some fraction Y (lying between 0 and 1) of that maximum, the equation determines the proportion of the population that will survive in the next season after reproduction and competition for food. Let’s suppose that each season the reproduction rate is given by a number r. If the fraction of the maximum population that survived to the end of the season was Y, the next generation would swell to r x Y x N.
But not all of these new animals will survive. The equation determines that the fraction that will not survive is also given by Y. So out of the r x Y x N animals that start the season, Y x (r x Y x N) die. So the total left at the end of the season is (r x Y x N)—(r x Y2 x N) = [r x Y x (1—Y)] x N, which means that the fraction of the maximum population that exists in the current season is r x Y x (1—Y).
Essentially, the model assumes that at the end of each season the surviving population is multiplied by a constant factor, called r (the reproduction rate) to produce the number of animals that will be alive at the beginning of the next season. But there aren’t enough resources for all of them to survive. The equation then calculates how many of these animals will make it until the end of the season. The resulting number is then multiplied by r again for the next generation. The fascinating property of this equation is that its behavior really depends only on the choice of r, the reproduction rate. Some choices of r lead to extremely predictable behaviors. I can know exactly how the numbers will evolve. But there is a threshold beyond which I lose control. Knowledge is no longer within reach; the addition of one extra animal into the mix can result in dramatically different population dynamics.
May discovered that if r lies between 1 and 3, the population eventually stabilizes. Regardless of the initial conditions, the numbers will gradually tend to be a fixed value. It’s like playing billiards on a table with a sinkhole in the middle. However I shoot the ball, it eventually finds its way to the bottom of the sinkhole.
For r above 3, we still see a region of predictable behavior, but of a slightly different character. If r remains between 3 and 1 + √6 (approximately 3.44949) the population dynamics ping-pong between two values that depend on r. As r passes 1 + √6, we see the population dynamics changing character again. For r between 1 + √6 and 3.54409 (or, more precisely, the solution of a polynomial equation of degree 12), there are four values that the population periodically cycles through. As r gets bigger, we get eight values, then sixteen, and so on. As r climbs, the number of different values doubles each time until we hit a threshold moment, when the dynamic flips from periodic to chaotic.
When May first explored this equation, he admitted that he frankly hadn’t a clue what was going on beyond this point—he had a blackboard outside his office in Sydney on which he offered a prize of ten Australian dollars to anyone who could explain the behavior of his equation. He wrote on the blackboard, “It looks like a mess.”
He got his answer on a visit to Maryland. This was, in fact, when the term “chaos” was actually coined. In a seminar, he explained his findings but admitted he’d hit a point beyond which he didn’t know what the hell was happening. In the audience was a mathematician who did know. Jim Yorke had never seen the doubling behavior, but he knew exactly what was going on in this higher region. And it was what he called chaos.
Beyond r = 3.56995 (or, more precisely, the limit point of a system of equations of increasing degree), the result becomes very sensitive to what the initial population looks like. Change the initial number of animals by a minute amount and a totally different result can ensue.

Two populations with r = 4 that start off with a difference of just one animal in a thousand. Although they start behaving similarly, by year 15 they are demonstrating very different behaviors.
As I turn up the dial on r, there can still be pockets of regular behavior, as Jim Yorke had discovered. For example, take r = 3.627 and the population becomes periodic again, bouncing around between six different values. Keep dialing r up and the six changes to twelve, which becomes twenty-four, doubling each time until chaos strikes again.
Bob May recognized just what a warning shot such a simple system was to anyone who thought they knew it all: “Not only in research, but in the everyday world of politics and economics, we would be better off if more people realized that simple systems do not necessarily possess simple dynamic properties.”
THE POLITICS OF CHAOS
Bob May is currently practicing what he preaches. Or perhaps I should say Lord May of Oxford, as I was corrected by a man in a top hat who greeted me at the door to the entrance of the House of Lords. May has in recent years combined his scientific endeavors with energetic political activism. He now sits as a cross-party member of the House of Lords, where I popped in for lunch to find out how he was faring in his mission to alert politicians to the impact of chaotic systems on society.
Ushered through the entrance to the Lords by the man in the top hat and policemen with machine guns, I found May waiting for me on the other side of metal detectors and X-ray machines. May has no truck with all these formal titles and, in his earthy Australian manner, still insists on being called Bob. “I’m afraid I messed up and already ate lunch but I’ll come and eat cake while you get some lunch,” he said with a guileless smile. As I ate my fish he consumed an enormous piece of chocolate cake. At seventy-nine, May is as energetic and engaged as ever, and he was rushing off after his second lunch to a select committee discussing the impact of a new rail link between London and northwest England. Before joining the Lords, May was chief scientific adviser both to John Major’s Conservative government and Tony Blair’s Labor government. I asked how tricky a balancing act such a political position is for a man who generally is not scared to tell it like it is.
“At the interview I was told that there would be occasions where I would be called upon to defend the decisions of a minister and how would I feel about that? I said that I would never under any circumstances deny a fact. On the other hand, I’m fairly good at the kind of debating competition where you’re given a topic and according to a flip of a coin you’ve got to argue for either side of the debate. So I said I’d be happy explaining why the minister’s choice was arrived at. I simply wouldn’t agree to endorse it if it wasn’t right.”
A typical mathematician’s response. Set up the minister’s axioms and then demonstrate the proof that led to the conclusion—a judgment-free approach. That’s not to say that May isn’t opinionated and prepared to give his own views on the subject at hand.
I was curious as to how governments deal with the problems that chaos theory creates when trying to make policy decisions. How do politicians cope with the challenges of predicting or manipulating the future, given that we can have only partial knowledge of the systems being analyzed?
“I think that’s rather a flattering account of what goes on here,” he said. “With some notable exceptions it’s mostly a bunch of very egotistical people, very ambitious people, who are primarily interested in their own careers.”
What about May personally? What impact did the discoveries he’d made have on his view of science’s role in society?
“It was weird. It was the end of the Newtonian dream. When I was a graduate student it was thought that with better and better computer power we would get better and better weather predictions because we knew the equations and we could make more realistic models of the Earth.” But May is cautious not to let the climate change deniers use chaos theory as a way to undermine the debate.
“Not believing in climate change because you can’t trust weather reports is a bit like saying that because you can’t tell when the next wave is going to break on Bondi beach you don’t believe in tides.”
May likes to quote a passage from Tom Stoppard’s play Arcadia to illustrate the strange tension that exists between the power of science to know some things with extraordinary accuracy and chaos theory, which denies us knowledge of many parts of the natural world. One of the protagonists, Valentine, declares, “We’re better at predicting events at the edge of the galaxy or inside the nucleus of an atom than whether it’ll rain on auntie’s garden party three Sundays from now.” May jokes that his most cited works are not the high-profile academic papers he’s published in prestigious scientific journals like Nature, but the program notes he wrote for Stoppard’s play when it was first staged at the National Theater in London. “It makes a mockery of all these citation indexes as a way of measuring the impact of scientific research.”
So what are the big open questions of science that May would like to know the answer to? Consciousness? An infinite universe?
“I think I’d look at it in a less grand way, so I’d look at it more in terms of the things I am working on at the moment. Largely by accident I’ve been drawn into questions about banking.”
That was a surprise. The question of how to create a stable banking system seemed very parochial, but May has recently been applying his models of the spread of infectious diseases and the dynamics of ecological food webs to understanding the banking crisis of 2008. Working with Andrew Haldane at the Bank of England, he has been considering the financial network as if it were an ecosystem. Their research has revealed how financial instruments intended to optimize returns with seemingly minimal risk can cause instability in the system as a whole.
May believes that the problem isn’t necessarily the mechanics of the market itself. It’s the way small things in the market are amplified and perverted by how humans interact with them. For him, the most worrying thing about the banking mess is getting a better handle on this contagious spreading of worry.
“The challenge is: How do you put human behavior into the model? I don’t think human psychology is mathematizable. Here we are throwing dice with our future. But if you’re trying to predict the throw of the dice, then you want to know the circumstance of who owns the dice.”
That was something I hadn’t taken into account. Perhaps I should factor in who sold me the casino die in the first place.
“I think many of the major problems facing society are outside the realm of science and mathematics,” he said. “It’s the behavioral sciences that are the ones we are going to have to depend on to save us.”
Looking around the canteen at the House of Lords, you could see the sheer range and complexity of human behavior at work. It makes the challenge of mathematizing even the interactions in this tiny microcosm of the human population well nigh impossible. As the French historian Fernand Braudel explained in a lecture on history he gave to his fellow inmates in a German prison camp near Lübeck during World War II, “An incredible number of dice, always rolling, dominate and determine each individual existence.” Although each individual throw is unpredictable, patterns still emerge in the long-range behavior of many throws of the dice. In Braudel’s view, this is what makes the study of history possible: “History is indeed ‘a poor little conjectural science’ when it selects individuals as its objects . . . but much more rational in its procedure and results when it examines groups and repetitions.”
May believes that understanding the history and origins of the collection of dice that make up the human race is not as straightforward as Braudel makes out. To his mind, it’s not at all clear that we can unpick how we got to this point in our evolutionary journey.
“I’ll tell you one of the questions that I think is a particularly interesting one: trying to understand our evolutionary trajectory as humans on our planet. Is the trajectory we seem to be on what happens on all or most planets, or is it the result of earlier fluctuations in the chaos which took us on this trajectory rather than another? Will we ever know enough to be able to ask whether the disaster we seem to be heading for is inevitable or whether there are lots of other planets where people are more like Mr. Spock, less emotional, less colorful, but much more detached and analytical?”
Until we discover other inhabited planets and can study their trajectories, it’s difficult to assess whether evolution inevitably leads to mismanaged ecosystems based on just one dataset called Earth.
“The question of whether where we’re heading is something that happens to all inhabited planets or whether there are other planets where it doesn’t happen is something I think we’ll never know.” And with that, May polished off the last few crumbs of his chocolate cake and plunged back into the chaos of the select committees and petty politics of Westminster.
May’s last point relates to the challenge that chaos theory poses for knowing something about the past as much as the future. At least with the future we can wait and see what the outcome of chaotic equations produces. But trying to work backward and understand what state our planet was in to produce the present is equally if not more challenging. The past, even more than the future, is probably something we can never truly know.
LIFE: A CHANCE THROW OF THE DICE?
May’s pioneering research explored the dynamics of a population as it went from season to season. But what determines which animals survive and which will die before reproducing? According to Darwin, this is simply down to a lucky roll of the evolutionary dice.
Darwin’s model for the evolution of life on Earth is based on the idea that once you have organisms with DNA, then the offspring of these organisms share the DNA of their parent organisms. Parts of the genetic code in the DNA can undergo random mutations. These are essentially down to the chance throw of the evolutionary dice. But there is a second important strand to Darwin’s proposal, which is the idea of natural selection. Some of those random changes will give offspring an increased chance of survival, while others will result in a disadvantage. The point of evolution by natural selection is that the organism with the advantageous change will be more likely to survive long enough to reproduce.
Suppose, for example, that I start with a population of giraffes with short necks. The environment of the giraffes changes such that there is more food in the trees, so that any giraffe born with a longer neck is going to have a better chance of survival. Let’s suppose that I throw my Vegas die to determine the chance of a mutation for each giraffe born in the next generation following this environmental change. A roll of a 1, 2, 3, 4, or 5 condemns the giraffe to a neck of the same size or shorter, while a throw of a 6 corresponds to a chance mutation that causes a longer neck. The lucky longer-necked giraffes get the food, and the shorter-necked giraffes don’t survive to reproduce. So it is just the longer-necked giraffes that get the chance to pass on their DNA.
In the next generation the same thing happens. Roll a 1, 2, 3, 4, or 5 on the die and the giraffe doesn’t grow any taller than its parents. But another 6 and the giraffe’s neck grows a bit more. The taller giraffes survive again. The environment favors the giraffes that have thrown a 6. Each generation ends up a bit taller than the last generation until there comes a point when it is no longer an advantage to grow any further.
The combination of chance and natural selection results in our seeing more giraffes with ancestors that all threw 6s. In retrospect it looks like amazing serendipity that you would see so many 6s in a row. But the point is that you don’t see any of the other rolls of the dice because they don’t survive. What looks like a rigged game is just the result of the combination of chance and natural selection. There is no grand design at work. The run of consecutive 6s isn’t a lucky streak; it is the only thing we would expect to see from such a model.
It’s a beautifully simple model, but, given the complexity of the changes in the environment and the range of mutations that can occur, this simple model can produce extraordinary complexity, which is borne out by the sheer variety of species that exist on Earth. Although the model is simple, it is frustratingly inadequate at making predictions. One of the reasons I never really fell in love with biology is that there seemed to be no way to explain why we got cats and zebras out of this evolutionary model and not some other strange selection of animals. It all seemed so arbitrary, so random. But is that really right?
There is an interesting debate going on in evolutionary biology about how much chance there is in the outcomes we are seeing. If we rewound the story of life on Earth to some point in the past and threw the dice again, would we see very similar animals appearing or could we get something completely different? This is the question that May raised at the end of our lunch.
It does appear that some parts of our evolutionary process seem inevitable. It is striking that throughout evolutionary history, the eye evolved independently fifty to a hundred times. This is strong evidence for the fact that the different rolls of the dice that have occurred across different species seem to have produced species with eyes regardless of what is going on around them. Lots of other examples illustrate how some features, if they are advantageous, seem to rise to the top of the evolutionary swamp. This is illustrated every time you see the same feature appearing more than once in different parts of the animal kingdom. Dolphins and bats, for example, use echolocation, but they evolved this trait independently at very different points on the evolutionary tree.
But it isn’t clear how far these outcomes are guaranteed by the model. If there is life on another planet, will it look anything like the life that has evolved here on Earth? This is one of the big open questions in evolutionary biology. As difficult as it may be to answer, I don’t believe it qualifies as something we can never know. It may remain something we will never know, but there is nothing by its nature that makes it unanswerable.
Are there other great unsolved questions of evolutionary biology that might be contenders for things we can never know? For example, why, 542 million years ago, at the beginning of the Cambrian period, was there an explosion in the diversity of life on Earth? Before this moment life consisted of single cells that collected into colonies. But over the next twenty-five million years, a relatively short period on the scale of evolution, there is a rapid diversification of multicellular life that ends up resembling the diversity that we see today. An explanation for this exceptionally fast pace of evolution is still missing. This is in part due to lack of data from that period. Can we ever recover that information, or could this always remain a mystery?
Chaos theory is usually a limiting factor in what we can know about the future. But it can also imply limits on what we can know about the past. We see the results, but deducing the cause means running the equations backward. Without complete data, the same principle applies backward as forward. We might find ourselves at two very divergent starting points that can explain very similar outcomes. But we’ll never know which of those origins was ours.
One of the big mysteries in evolutionary biology is how life got going in the first place. The game of life may favor runs of 6s on the roll of the evolutionary dice, but how did the game itself evolve? Various estimates have been proposed for the chances of everything lining up to produce molecules that replicate themselves. In some models, the origin of life is equivalent to nature having thrown thirty-six dice and getting them all to land on 6. For some, this is proof of the existence of God or of some form of a grand designer to rig the game. But this is to misunderstand the huge time scale that we are working on.
Miracles do happen . . . given enough time. Indeed, it would be more striking if we didn’t get these anomalies. The point is that the anomalies stick out. They get noticed, while the less exciting rolls of the dice are ignored.
The lottery is a perfect test bed for the occurrence of miracles in a random process. On September 6, 2009, the following six numbers were the winning numbers in the Bulgarian state lottery: 4, 15, 23, 24, 35, 42. Four days later, the same six numbers came up again. Incredible, you might think. The government in Bulgaria certainly thought so and ordered an immediate investigation into the possibility of corruption. But what it failed to take into account is that each week, across the planet, different lotteries are being run. They have been running for decades. If you do the math, it would be more surprising not to see such a seemingly anomalous result.
The same principle applies to the conditions for producing self-replicating molecules in the primeval soup that made up the Earth before life emerged. Mix together plenty of hydrogen, water, carbon dioxide, and some other organic gases and subject them to lightning strikes and electromagnetic radiation, and already experiments in the lab show the emergence of organic material found only in living things. No one has managed to spontaneously generate anything as extraordinary as DNA in the lab. The chances of that are very small.
But that’s the point. Given the billion billion or so possible planets available in the universe on which to try out this experiment, together with a billion or so years to let the experiment run, it would be more striking if that outside chance of creating something like DNA didn’t happen. Keep rolling thirty-six dice on a billion billion different planets for a billion years and you’d probably get one roll with all thirty-six dice showing 6. Once you have a self-replicating molecule, it has the means to propagate itself, so you only need to get lucky once to kick off evolution.
THE FRACTAL TREE OF LIFE
Our problem as humans is that we have not evolved minds able to navigate very large numbers. Probability is something we have little intuition for. But it’s not only the mathematics of probability that is at work in evolution. The evolutionary tree itself has an interesting quality that it shares with chaos theory. This quality is known as a fractal.

The fractal evolutionary tree
The evolutionary tree is a graphic representation of the evolution of life on Earth. Each time the tree branches, this represents the evolution of a new species. If a branch terminates, this means the extinction of that species. The nature of the tree is such that the overall shape seems to be repeated on smaller and smaller scales. This is the characteristic feature of a shape mathematicians call a fractal. If you zoom in on a small part of the tree it looks remarkably like the large-scale structure of the tree. This self-similarity means that it is very difficult to tell at what scale we are looking at the tree. This is the classic characteristic of a fractal.
Fractals are the geometric signature of a chaotic system, so it is suggestive of chaotic dynamics at work in evolution: small changes in the genetic code can result in huge changes in outcome. This model isn’t necessarily a challenge to the idea of convergence, as there can still be points in chaotic systems toward which the model tends to evolve. Such points are called attractors. But it certainly questions whether if you reran evolution it would look anything like what we’ve got on Earth today. The evolutionary biologist Stephen Jay Gould contended that if you were to rerun the tape of life, you would get very different results. This is what you would expect from a chaotic system. Just as with the weather, very small changes in the initial conditions can result in dramatically different outcomes.
Gould introduced the idea of punctuated equilibria to capture the fact that species seem to remain stable for long periods and then undergo what appears to be quite rapid evolutionary change. This has been shown to be a feature of chaotic systems. The implications of chaos at work in evolution could well fall under the umbrella of things we cannot know.
Will we ever know whether humans were destined to evolve? An analysis of DNA in different animals has given us exceptional insights into the way animals have evolved in the past. The fossil record, although incomplete in places, has also given us a way to know our origins. But given the time scales involved in evolution, it is impossible to experiment and rerun the tape of life and see whether something different could have happened. As soon as we find life on other planets (if we do), this will give us new sample sets to analyze. But until then all is not lost. Just as the National Weather Service doesn’t have to run real weather to make predictions, computer models can illustrate different possible outcomes of the mechanism of evolution by speeding up time. But the model will only be as good as our hypotheses. If we’ve got the model wrong, it won’t tell us what is really happening in nature.
Computer models such as these hold the key to answering the question Poincaré first tackled when he discovered chaos: Will there even be a stable Earth orbiting the sun for evolution to continue playing its game of dice? How safe is our planet from the vagaries of chaos? Is our solar system stable and periodic, or do I have to worry about a grasshopper disrupting our orbit around the sun?
A BUTTERFLY CALLED MERCURY
Poincaré wasn’t able to answer the King of Sweden’s question about the solar system, that is, whether it would remain in a stable equilibrium or fly apart in a catastrophic exhibition of chaotic motion. His discovery that some dynamic systems can be sensitive to small changes in data opened up the possibility that we may never know the precise fate of the solar system much in advance of any potentially devastating scenario unfolding.
It is possible that the solar system is in a safe, predictable region of activity, but the evidence suggests we can’t console ourselves with this comforting mathematical hope. Recent computer modeling has provided us with new insights, which reveal that the solar system is indeed within a region dominated by the mathematics of chaos. We can now measure how big an effect a small change will have on the outcome of a closed system using something called the Lyapunov exponent. If the Lyapunov exponent is positive, it means that if I make a small change in the initial conditions then the distance between the paths will diverge exponentially.
Using this new equation, several groups of scientists have confirmed that our solar system is indeed chaotic. They have calculated that the distance between two initially close orbital solutions increases by a factor of ten every ten million years. This is certainly on a different timescale to our inability to predict the weather. Nevertheless, it means that I can have no definite way of knowing what will happen to the solar system over the next five billion years.
If you’re wondering in despair whether we can know anything about the future, then take heart in the fact that mathematics isn’t completely hopeless at making predictions. There is an event that the equations guarantee will occur if we make it to five billion years from now, but it’s not good news. At this point, the sun will run out of fuel and evolve into a red giant that will engulf Earth and the other planets in our solar system. But until this solar blowout, I am faced with trying to solve chaotic equations if I want to know which planets will still be around to see that red giant.
If I want to know what will happen, I have no choice but to run simulations in which I vary the precise locations and speeds of the planets. The forecast is in some cases rather frightening. In 2009 French astronomers Jacques Laskar and Mickael Gastineau ran several thousand models of the future evolution of our solar system. Their experiments have identified a potential butterfly: Mercury.
The simulations start by feeding in the records we have of the positions and velocities of the planets to date, but it is difficult to know these with one hundred percent accuracy. So each time they run the simulation they make small changes to the data. Because of the effects of chaos theory, a small change could result in a large deviation in the outcomes.
For example, astronomers know the dimensions of the ellipse of Mercury’s orbit to an accuracy of several meters. Laskar and Gastineau ran 2,501 simulations varying these dimensions over a range of less than a centimeter. Even this small perturbation resulted in startlingly different outcomes for our solar system.
If the solar system were to be ripped apart, you might expect one of the big planets, like Jupiter or Saturn, would be the culprit. But the orbits of the gas giants are extremely stable. It’s the rocky terrestrial planets that are the troublemakers. In one percent of simulations, Laskar and Gastineau found that tiny Mercury posed the biggest risk. The models show that Mercury’s orbit could start to extend due to a certain resonance with Jupiter, with the possibility that Mercury could collide with its closest neighbor, Venus. In one simulation, a close miss was enough to throw Venus out of kilter, with the result that Venus collides with Earth. Even close encounters with the other planets would be enough to cause such tidal disruption that the effect would be disastrous for life on our planet.
This isn’t simply a case of abstract mathematical speculation. Evidence of such collisions has been observed in the planets orbiting the binary star Upsilon Andromedae. Their current strange orbits can be explained only by the ejection of an unlucky planet sometime in the star’s past. But before we head for the hills, the simulations reveal that it will take several billion years before Mercury might start to misbehave.
INFINITE COMPLEXITY
What of my more modest goal of predicting the throw of my die? Laplace would have said that provided I can know its dimensions, the distribution of its atoms, the speed at which it is launched, and its relationship to its surrounding environment, theoretically the calculation is possible. But the discoveries of Poincaré and those who followed have revealed that just a few decimal places could be the difference between a 6 or a 2. The die is designed to have only six different outcomes, yet the input data range over a potentially continuous spectrum of values. The question is whether the dynamics of the die are truly chaotic—or could they be simpler than one might expect? If I vary the angle at which the die leaves my hand, is there a moment when the outcome flips from a 6 to a 2, or is it much more sensitive to small changes?
A Polish research team recently analyzed the throw of a die mathematically, and by combining this with the use of high-speed cameras they have revealed that my die may not be as chaotic and unpredictable as I feared. It just depends on the conditions of the table onto which you are throwing your die. The research group consists of a father-and-son team, Tomasz and Marcin Kapitaniak, together with Jaroslaw Strzalko and Juliusz Grabski, and they are based in Lódź. The model they considered, published in a paper in the journal Chaos in 2012, assumes that the die is perfectly balanced, like the one I brought back from Vegas. Air resistance, it turns out, can be ignored, as it has very little influence on our cube as it tumbles through the air. When it hits the table a certain proportion of its energy is dissipated, so that after a number of bounces it has lost all kinetic energy and comes to a rest. (Friction on the table is also key, as the die is likely to slide only in the first few bounces, but the model explored by the Polish team assumed a frictionless surface, as the dynamics get too complicated to handle when friction is present. So imagine throwing your dice onto an ice rink.)
I’d already written down equations based on Newton’s laws of motion to calculate the dynamics of the die as it flies through the air. In the hands of the Polish team they turn out not to be too complicated, but the equations for the change in dynamics after the impact with the table are pretty frightening, taking up ten lines of their paper.
The paper includes pictures that describe the outcome of their experiments. The Polish team investigated the effect of varying two parameters: the height from which the die was launched and the angular velocity around one of the axes. They gave each face of the die its own color and constructed a picture that took each coordinate in the diagram and colored it according to the face of the die that resulted from launching it within the parameters corresponding to that coordinate. So if the resulting picture is fractal—meaning that however much I zoom in, I still see regions containing at least two colors—then the outcome of the roll of the die is impossible to predict. The Polish team tried throwing their dice on different types of tables. They discovered that if the amount of energy dissipated on impact with the table is quite high, the picture of the outcome does not have a fractal quality. This means that if one can settle the initial conditions with appropriate accuracy, the outcome can be predictable and repeatable. This predictability implies that more often than not, the dice will land on the face that was lowest when they were launched. A die that is fair when static may actually be biased when one adds in its dynamics.
As the table becomes more rigid, resulting in less energy being dissipated and hence more bouncing, I start to see a fractal quality emerging.

Moving from (a) to (d), the table dissipates less energy, resulting in a more fractal quality for the outcome of the dice.
So the bottom line is look for a casino whose craps tables have thick felt that might absorb the energy of the die as it hits the table. The less energy that is dissipated on impact with the table, the more chaotic its resulting behavior and the more it seems that the outcome recedes back into the hands of the gods.
There is an important message here. Dynamical systems like the weather, population growth, the economy, or the fall of my die can have regions that are very predictable and knowable. Throw the die on a table that causes the die to lose energy and the behavior of the die is not chaotic. Approximate knowledge of how the die is launched will be enough to calculate its outcome. But there are other conditions under which these dynamical systems become chaotic and unknowable. The trick is knowing for any dynamical system the moment when it flips from being predictable to chaotic, knowing when you can’t know what is going to happen next.
DOES GOD PLAY DICE?
In the deep past, gods weren’t considered to be supernatural intelligences living outside the system. They were rivers, the wind, fire, the sun—things that could not be predicted or controlled. They lived in the realm of chaos. Twentieth-century mathematics has revealed that these ancient gods are still with us. There are natural phenomena that will never be tamed and known. Chaos theory asserts that I cannot know the future of certain systems because they are too sensitive to small inaccuracies. Because we can never have complete knowledge of the present, chaos theory denies us access to the future.
That’s not to say that all futures are unknowable. Very often we are in regions that aren’t chaotic, where small fluctuations have little effect. This is why mathematics has been so powerful in helping us to predict and plan. The power of mathematical equations has allowed us to land spaceships on other planets, predict the paths of deadly typhoons on Earth, and model the effects of deadly viruses, allowing us to take action before they become a pandemic. But at other times we cannot accurately predict or control outcomes.
Some religious commentators who know their science and seek to offer a scientific explanation for how a supernatural intelligence could act in a scientific world have intriguingly tried to use the gap that chaos provides as a space for this intelligence to affect the future. One of these is the quantum physicist John Polkinghorne. Based at the University of Cambridge, Polkinghorne is a rare man who combines both the rigors of a scientific education with years of training to be a Christian priest. I will return to Polkinghorne in the Third Edge, when I explore the unknowability inherent in his own scientific field of quantum physics, but he has also been interested in the gap in knowledge that the mathematics of chaos theory provides as an opportunity for God to influence the future course of humanity.
Polkinghorne has proposed that a supernatural intelligence can still act without violating the laws of physics via the indeterminacies implicit in chaos theory. Chaos theory says that we can never know the setup precisely enough to be able to run deterministic equations, and hence there is room in Polkinghorne’s view for divine intervention, to tweak things in such a way as to remain consistent with our partial knowledge but still influence outcomes.
Polkinghorne is careful to stress that to use infinitesimal data to effect change requires a complete holistic top-down intervention. This is not a God in the details but an all-knowing God. Given that chaos theory means that even the location of an electron on the other side of the universe could influence the whole system, we need to have complete, holistic knowledge of the system—the whole universe—to be able to steer things. We cannot successfully isolate a part of the universe and hope to make predictions based on that part. So it would require knowledge of the whole to act via this tiny chink.
Polkinghorne’s take on how to square the circle of determinism and influence is to use the gap between epistemology and ontology—in other words, between what we know and what is true. It is important to recognize that chaos theory is deterministic. It is not random. Repeat the experiment with exactly the same starting conditions and the result will be the same each time. But since we cannot know with complete certainty the state of the universe at this moment in time, from our perspective there is no determinacy. Many different scenarios coincide with our impartial description of what we currently know about how the universe is set up. Polkinghorne’s contention is that at any point in time this gives God the chance to intervene and shift the system between any of these scenarios without our being aware of the shift. As we have seen, chaos theory means that these small shifts can still result in hugely different outcomes. Polkinghorne is careful to assert that there is change only in information, not energy. The goal here is not to violate any rules of physics. As Polkinghorne says, “The succession of the seasons and the alternations of day and night will not be set aside.”
Even if you think this is rather fanciful (as I do), a similar principle is key to our own feeling of agency in the world. Free will is related ultimately to the deep desire to challenge a belief in a reductionist philosophy. It makes sense to create a narrative in which we have free will because that is how we experience life. If things were obviously deterministic, we wouldn’t think that we had any meaningful choice. From a human perspective, we feel like we make meaningful choices every day. But perhaps that feeling is just a result of chaos theory masking our ability to see determinism at work in the world.
It is striking that Newton, the person who led us to believe in a clockwork deterministic universe, also felt that there was room in the equations for God’s intervention. He wrote of his belief that God would sometimes have to reset the universe when things looked like they were going off course. He got into a big fight with his German mathematical rival, Gottfried Leibniz, who couldn’t see why God wouldn’t have set things up perfectly from the outset. In Leibniz’s view, “Sir Isaac Newton and his followers have also a very odd opinion concerning the work of God. According to their doctrine, God Almighty wants to wind up his watch from time to time: otherwise it would cease to move. He had not, it seems, sufficient foresight to make it a perpetual motion.”
Newton’s calculus gave me a feeling that I could know the future, that I could shortcut the wait for it to become the present. But the mathematics of the twentieth century revealed that theory doesn’t necessarily translate into practice. Even if Laplace is correct that complete knowledge of the current state of the universe should lead to complete knowledge of the future, I will never have access to that complete knowledge. The shocking revelation of twentieth-century chaos theory is that even an infinitesimally small approximation can change everything. The divergent paths of the chaotic billiard table mean that since we can never know which path we are on, our future is not predictable.
The mathematics in which I had placed so much faith revealed its own limitations. But the situation is not entirely hopeless. Many times equations are not sensitive to small changes and hence do give us access to predictions about the future. After all, this is how we landed a spaceship on a passing comet.
It is striking to listen to Laplace on his deathbed. With only a finite amount of time to go, he admitted, “What we know is little, and what we are ignorant of is immense.” It isn’t just the outward behavior of planets that is unknowable. Probing deep inside my casino die reveals another challenge to Laplace’s belief in a clockwork universe.