4

Everything we call real is made of things that cannot be regarded as real.

—Niels Bohr

THE REALIZATION THAT protons and neutrons might not be indivisible came not from new and more sophisticated technology, but from the mathematics of symmetry. It is striking that time and again, mathematics appears to be the best lens we have to peer into the mysteries of science. The mathematical model responsible for our belief in the divisibility of the proton and neutron arose shortly after physicists discovered that there were many more particles out there than the three that were believed to be the constituent parts of stable atoms. The discovery of these new particles emerged from the study of collisions that happen in the upper atmosphere when cosmic rays strike the atmosphere.

The first evidence of new particles was found in the cloud chambers that scientists had built in their labs to record the path of charged particles. (Cloud chambers are sealed tanks full of a supersaturated vapor of water and alcohol; the supersaturation is such that any charged particle passing through it leaves a trail of condensation.) Carl Anderson, a physicist working at the California Institute of Technology, had used cloud chambers in 1933 to confirm the existence of a strange new thing called antimatter, first predicted some years earlier by British physicist Paul Dirac. Dirac’s attempt to unify quantum physics and the theory of electromagnetism had successfully explained many things about electrons, but it had also suggested something that didn’t correspond to anything anyone had seen in the lab.

Dirac’s equations were a bit like the equation x2 = 4. The obvious solution is x = 2, but there is also another mirror solution, namely x = –2, because –2 × –2 is also equal to 4. The mirror solution in Dirac’s equations suggested that there might be a mirror version of the electron with a positive charge. Most thought this was a mathematical curiosity with no basis in reality, but when, four years later, Anderson spotted in his cloud chamber traces of a particle behaving like an electron in a mirror, antimatter went from theory to reality. Anderson’s “positrons,” as they came to be known, could be found in the particle interactions happening in the upper atmosphere. And they weren’t the only new things to appear.

Even stranger particles were soon leaving trails in Anderson’s cloud chamber. Anderson started to analyze these unanticipated negatively charged new particles with his doctoral student Seth Neddermeyer in 1936. The paths they were leaving indicated that their mass was much larger than that of an electron (mass can be measured by how much a particle is deflected under the influence of a magnetic field). The particle seemed to have the same charge as the electron, but it was much harder to deflect.

The muon, as this particle is now called, was one of the first new particles to be discovered in the interactions of cosmic rays with the atmosphere. The muon is unstable. It quickly falls apart, most often into an electron and a couple of neutrinos (another new particle, first detected in the 1950s) with almost no mass and no charge. Neutrinos made sense both of neutron decay and of the decay of this new muon. The decay rate of the muon was on average 2.2 microseconds, slow enough for some particles to still be around when they reached the surface of the Earth.

The muon helped confirm Einstein’s prediction that time slows down as you approach the speed of light. Given its half-life, far fewer muons should be reaching the surface of the Earth than were being detected. The fact that time slows down close to the speed of light helped explain this discrepancy. I will return to this in the Fifth Edge, when we consider pushing time to the limits of knowledge.

The muon behaved remarkably like the electron, but it had greater mass and was less stable. When the American physicist Isidor Rabi was told of the discovery, he said, “Who ordered that?” It seemed strangely unnecessary for nature to introduce a heavier, less stable version of the electron. Little did Rabi realize how much more there was on the menu.

Having realized that the interactions of cosmic rays with the upper atmosphere were creating new forms of matter, physicists decided that they had better not wait for these particles to reach the cloud chambers in their labs, by which time they might have decayed into traditional forms of matter. So the cloud chambers were moved to high-altitude locations in the hope of picking up other particles.

The Caltech team chose the top of Mount Wilson, near their home base in Pasadena. Sure enough, new tracks indicated that new particles were being picked up. Other teams placed photographic plates in observatories in the Pyrenees and the Andes to see if they could record different interactions. It turned out that the muon was the least of Rabi’s worries. A whole menagerie of new particles started showing up.

Some had masses about one-eighth that of a proton or neutron. They came in positively or negatively charged varieties and were dubbed pions. An electrically neutral version, harder to detect, was later discovered. In Manchester two photographs showed what appeared to be a neutral particle decaying into pions. The mass of these new particles was roughly half that of a proton. The cloud chamber at the top of Mount Wilson recorded more evidence to support the discovery of what would soon become known as kaons.

As time went on, more and more particles were uncovered, so many that the whole thing became totally unwieldy. As Nobel Prize winner Willis Lamb quipped in his acceptance speech of 1955, “The finder of a new elementary particle used to be rewarded by a Nobel Prize, but such a discovery now ought to be punished by a $10,000 fine.” It had been hoped that the periodic table would be simplified once scientists had discovered how it was put together using electrons, protons, and neutrons. But these three particles turned out to be just the tip of the iceberg. Now there were more than a hundred particles that seemed to make up the building blocks of matter. Enrico Fermi went so far as to tell a student at the time, “Young man, if I could remember the name of these particles, I would have been a botanist.”

Just as Mendeleev had managed to find some sort of order with which to classify and make sense of the atoms in the periodic table, the search was on for a unifying principle that would explain these new muons, pions, kaons, and numerous other particles. The underlying structure that finally made sense of this menagerie of particles—the map, as it were, to the zoo—was ultimately discovered thanks to nimble mathematics.

MAPPING THE PARTICLE ZOO

When you are trying to classify things, whether plants, animals, or subatomic particles, it helps to recognize their dominant characteristics. In the case of animals, the concept of species offers some order in the animal kingdom. In particle physics, one of the characteristics that helped divide the zoo into smaller groups was the idea of charge. How does the particle interact with an electromagnetic force? Electrons would bend one way, protons the other, and the neutron would be unaffected. As new particles emerged, they could be filtered through the gateway of electromagnetic force. Some would join the electron’s cage, others would head toward the proton, and the rest would be put together with the neutron—a first pass at imposing some order on our particle menagerie.

Electromagnetic force is one of four fundamental forces identified as being at work in bringing the universe together. The other forces are gravity; the strong nuclear force responsible for binding protons and neutrons together at close quarters; and the weak nuclear force, which controls things like radioactive decay.

What other characteristics could distinguish the different behaviors of these new particles? It was soon found that the mass of a particle was actually quite a good way of establishing some hierarchy. Pions and kaons were a factor lighter than the protons or neutrons that made up ordinary matter, and could thus be collected together. But mass was a rather rough and ready way of sorting particles. Physicists were on the lookout for something more fundamental—a pattern as effective as the one Mendeleev had discovered with his periodic table.

The key to making sense of the onslaught of new particles was a new property called strangeness. The name arose due to the unusual behavior demonstrated by some of these new particles as they decayed. Because mass is equivalent to energy (this is the crux of Einstein’s equation E=mc2), and nature favors low-energy states, particles with larger mass often try to find ways to decay into particles with smaller mass.

There are several mechanisms for this decay, each of which depends on one of the four fundamental forces. Each mechanism has a characteristic signature, helping physicists to understand which fundamental force is causing the decay. Energy considerations determine the most likely force at work in the decay of any given particle. The strong nuclear force is usually the first to have a go at decaying a particle, and this will generally decay the particle within 10–24 of a second. Next in the hierarchy is electromagnetic force, which might result in the emission of photons. The weak nuclear force is the most costly in energy terms, and so it takes longer. A particle that decays via the weak nuclear force is likely to take 10–11 seconds to decay. That’s a factor of 10 trillion times slower. So by observing the time a particle takes to decay, scientists can get some indication of which force is at work.

Imagine a ball sitting in a valley flanked by two hills of differing sizes. There is a path to the right that, with a little push, will take the ball over the lower hill into a lower valley. This path corresponds to the strong nuclear force. To the left is a higher hill that also offers a path to the lower valley. This direction represents the work of the weak nuclear force.

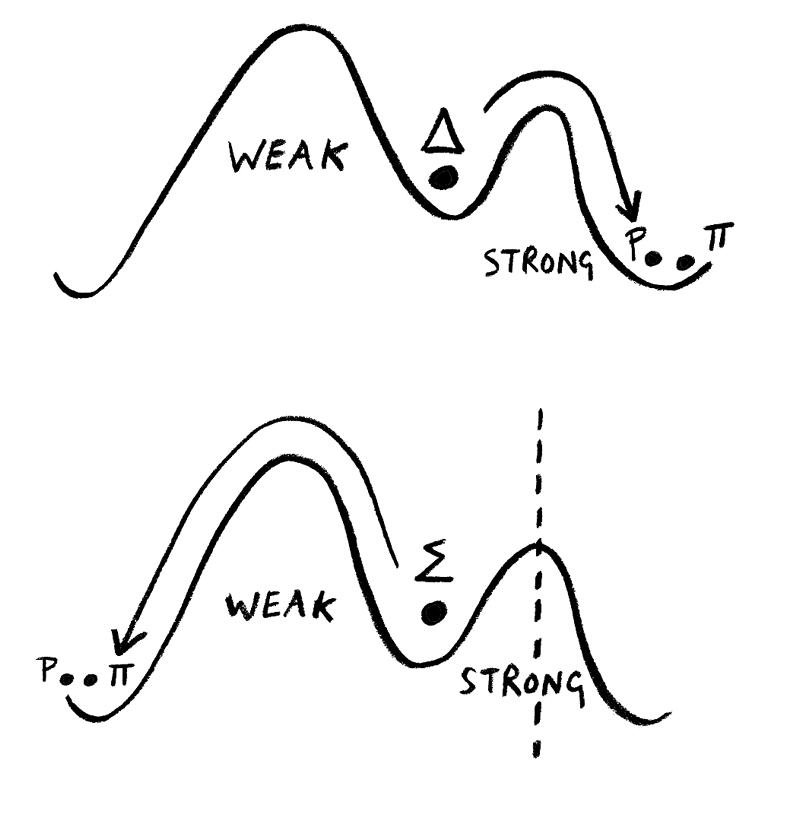
A Delta baryon ∆ decays via the strong nuclear force to a proton and a pion. In contrast, a Sigma baryon ∑ decays via the weak nuclear force.

So why do some particles find a way over the easy hill while others go the longer way? This seemed rather strange. Certain particles appeared to encounter a barrier (represented in the figure by a broken line) that prevented them from crossing via the easy route to the lower valley.

The physicists Abraham Pais, Murray Gell-Mann, and Kazuhiko Nishijima came up with a cunning strategy to solve this puzzle. They proposed a new property that mediated the way particles interacted with the strong nuclear force. This new property, called strangeness, gave physicists a new way to classify all these new particles. Each new particle was given a measure of strangeness according to whether it would have to take the long route to decay. The idea is that the strong nuclear force can’t change the strangeness of a particle, so if you have two particles with different strangeness, the strong nuclear force can’t decay one into another. But the weak nuclear force can change strangeness.

Then even more exotic particles were detected, created by higher-energy collisions that seemed to decay in two steps via the weak nuclear force. They were called cascade particles. The proposal was that these were doubly strange, so they were given strangeness number –2. The first step in the decay had been given a strangeness of –1 and after decaying again via the weak nuclear force the particles became protons and neutrons, which had strangeness 0. It may seem a bit like pulling a rabbit out of a hat, but that’s part of the process of doing science. You keep pulling stranger and stranger things out of your hat. Most you chuck away because they get you nowhere, but pull enough things out of the hat and every so often you’ll get a rabbit. As Gell-Mann later admitted, “The strangeness theory came to me when I was explaining a wrong idea to someone, but then I made a slip of the tongue and I had the strangeness theory.” Strangeness turned out to be a pretty amazing rabbit.

Originally the idea of strangeness was meant as a bookkeeping device, something that conveniently kept track of the decay patterns of different particles. It was just another set of cages to help classify the many animals in this particle zoo. But it transpired that this new feature was actually the first hint of a much deeper physical reality at work. The exciting moment came when scientists took particles of a similar mass and began to plot them on a graph measuring their strangeness and charge together. What they got were pictures full of symmetry.

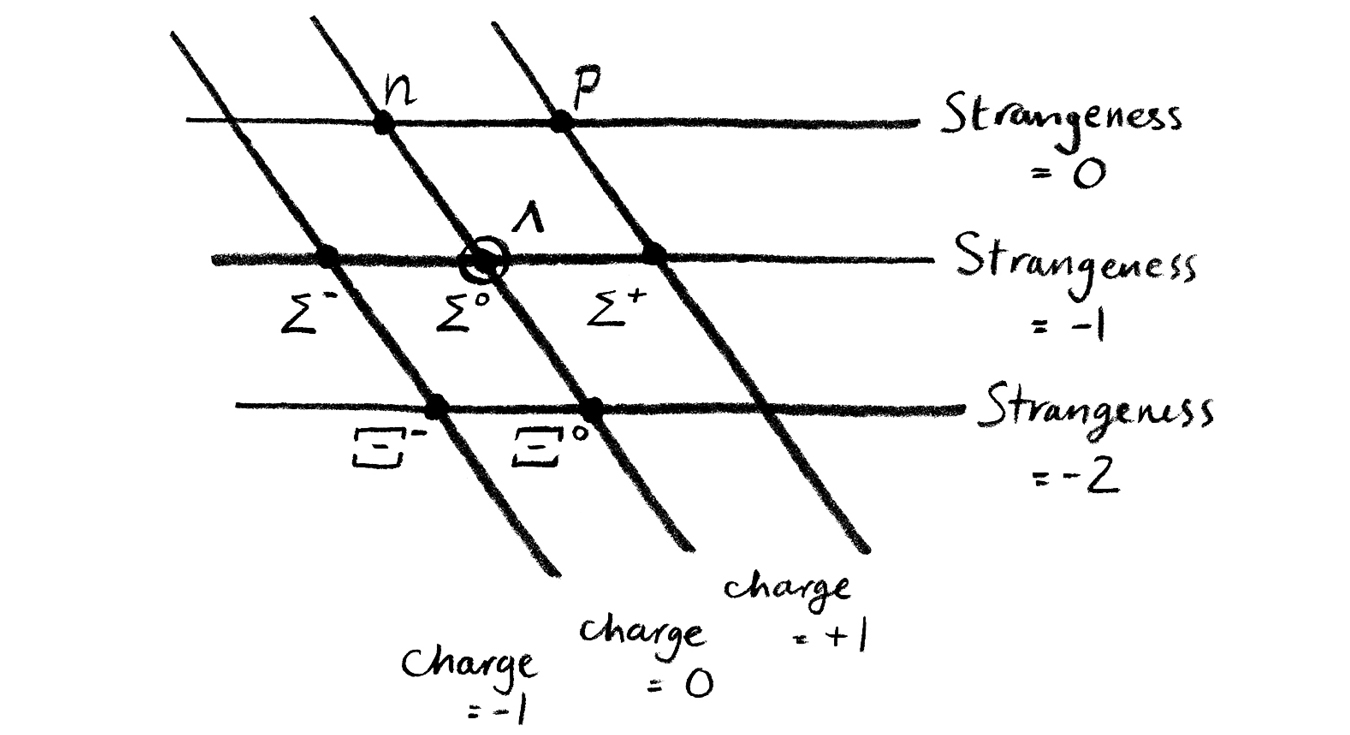
They found themselves with a hexagonal grid, with two particles occupying the center point of the grid. If one took pions and kaons and arranged them on a grid of strangeness against charge, a similar picture emerged. When you get a pattern like this you know you are on to something. The hexagonal patterns these particle pictures were making were not new—they’d been seen before. Not in physics, but in the mathematics of symmetry.

STRANGE SYMMETRIES

To someone trained in the mathematics of symmetry, these arrangements of cages in a hexagonal pattern with a double point at the center look very familiar. They are the signature of a very particular symmetrical object called SU(3). For me this is brilliant. Symmetry is something I know. It gives me a chance to get a handle on what is going on just when things are getting complicated. SU(3) stands for “the special unitary group in dimension 3,” but it can describe the symmetries of a range of different geometric objects in different dimensions. Although the objects can look very different, even existing in different dimensional spaces, their underlying symmetries can be the same. The hexagonal grids created by the particles are the same as the images mathematicians use to describe the way SU(3) acts on an object in eight-dimensional space. The eight particles of the hexagonal grid correspond to the number of dimensions you need to create this symmetrical object.

This hexagonal picture was the Rosetta Stone that opened up a whole new world in particle physics. The picture led physicists to the realization that the symmetry group SU(3) was the secret to understanding all these new particles. This new insight became known as “the eightfold way,” an invocation of the Buddhist idea of the eightfold way to spiritual enlightenment. Similar pictures, it was soon discovered, could be used to gather together other members of the particle menagerie. Each new picture corresponded to another object whose symmetries were described by SU(3). It was an extraordinary discovery. The fundamental particles were far from being a wild mess. They all seemed to be elements of geometries with a common symmetry.

It is amazing to me how, time and again, the physical world seems to be guided by mathematics. To what extent is it just a good story that helps us make sense of things? Is the physical universe actually a form of physicalized math? This is something I’ve been asking myself for a long time, and my journey thus far seems to suggest it might well be the case.

Heisenberg was right when he wrote, “Modern physics has definitely decided in favor of Plato. In fact, the smallest units of matter are not physical objects in the ordinary sense; they are forms, ideas which can be expressed unambiguously only in mathematical language.” Plato’s watery icosahedron and fiery tetrahedron have been replaced by the strange new symmetrical shape of SU(3).

When the physical world turns into a piece of mathematics, I immediately feel that this is something I can comprehend. The mathematics of symmetry is my language. For most people, turning fundamental particles into math means a move away from things they know. Comparing particles to billiard balls or waves gives them a more tangible sense of what is going on. Even the abstract language of eight-dimensional symmetrical objects is possible only because we are abstracting the ideas of things we have physically encountered.

Murray Gell-Mann and Yuval Ne’eman both independently recognized the patterns in these particles in 1961. Ne’eman combined his physics with a career in the Israeli Defense Force, and that year he had been posted to London as a military attaché. He’d meant to study general relativity at King’s College, but when he realized that it was miles from the Israeli Embassy in Kensington, he decided to check out what was happening five minutes down the road at Imperial College. It wasn’t long before he turned his attention from the very big to the very small.

Although the pattern for the lambda, sigma, and xi particles matched the eight-dimensional symmetry of SU(3), the corresponding pattern of kaons and pions was missing a particle at its center. It was either wrong or there was a new particle to be discovered. Gell-Mann published his prediction of a missing particle in a Caltech preprint in early 1961. Sure enough, physicists in Berkeley discovered the eta particle a few months later.

This is the perfect scenario for a new theory. If you make a prediction that is subsequently confirmed, you know you’re on to a winner. In June 1962, Gell-Mann and Ne’eman attended a conference together at CERN. At the conference, a whole host of new particles was announced: three sigma-star baryons with a strangeness of –1, and two xi-star baryons with a strangeness of –2. It was thought that these particles could be used to build a picture that corresponded to another geometric object that had the symmetries of SU(3).

As Gell-Mann and Ne’eman sat there in the lecture, they could both see this new picture emerging, except that one of the corners of the picture was missing. There were only nine particles. The picture should have had ten. Both Gell-Mann and Ne’eman simultaneously realized that one place had been left empty, leading to the prediction of a new particle. Gell-Mann stuck his hand up first and predicted the existence of a new omega particle with a strangeness of –3, a prediction that would be confirmed in January 1964.

It was a twentieth-century version of Mendeleev’s periodic table: the recognition of an underlying pattern with missing jigsaw pieces. Just as the discovery of the missing atoms gave credence to Mendeleev’s model, the discovery of these missing particles helped convince scientists that mathematical patterns were powerful ways to navigate the particle menagerie.

The patterns in the periodic table ultimately revealed that atoms were made up of protons, electrons, and neutrons. There was a feeling that the patterns of the newly discovered particles hinted at a similar story—the existence of still more fundamental building blocks.

QUARKS: THE MISSING LAST LAYER?

A number of physicists had noticed that if you place the different pictures that were emerging from all these new particles, you get a pyramid shape—with the top layer missing. If you looked at these layers from the perspective of symmetry, this missing layer, a single triangle, was really the one from which you could grow all the other layers. But no one had spotted any particles that corresponded to this missing layer.

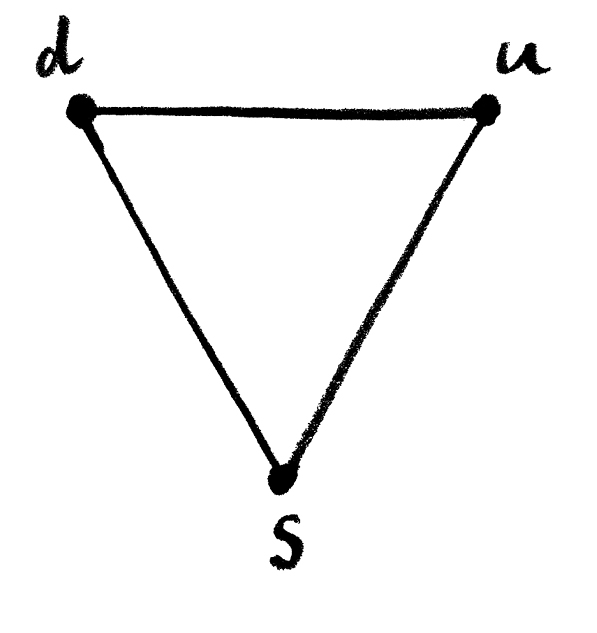
Triangle hinting at three new particles: the up quark u, the down quark d, and the strange quark s

Robert Serber, Oppenheimer’s right-hand man during the Manhattan Project, conjectured that maybe this extra layer suggested the existence of three new fundamental particles. At a lunch with Gell-Mann in 1963, Serber put forward his idea, but when Gell-Mann challenged him to explain what electrical charge these hypothetical particles would have, Serber wasn’t sure. Gell-Mann started scribbling on a napkin and soon he had the answer. The charges would be ⅔ or –1⁄3 of the charge on a proton. The answer seemed ridiculous. “That would be a funny quirk,” Gell-Mann commented. Nowhere in physics had anything been observed that wasn’t a whole-number multiple of the charge on the electron or proton.

No one had ever seen such a fractional charge. Although Gell-Mann was initially skeptical about these hypothetical particles with fractional charge, by the evening they began to work their magic on him. In the subsequent weeks he teased out the implications of these ideas, calling the particles “kworks” whenever he talked about them, a word he had used previously to denote “funny little things.” Serber believed the word was a play on the idea of the quirkiness Gell-Mann had mentioned at lunch.

It was while perusing James Joyce’s experimental novel Finnegans Wake that Gell-Mann came across a passage that determined how he would spell the word he was using to describe these hypothetical particles. The opening line of a poem ridiculing King Mark, the cuckolded husband in the Tristan myth, caught his attention: “Three quarks for Muster Mark!”

Given that there were three of these hypothetical new particles that could be used to build the other layers, the reference seemed perfect. The only trouble was that Joyce clearly intended the new word quark to rhyme with “Mark” not “kwork.” But the spelling and pronunciation Gell-Mann wanted won out.

These quarks would eventually become what we now believe to be the last layer in the construction of matter. But it would take some time for the idea to catch on. During a conversation on the telephone to his former PhD supervisor about these quarks, Gell-Mann was stopped in his tracks. “Murray, let’s be serious,” his supervisor told him. “This is an international call.”

For Gell-Mann, the patterns seemed too beautiful not to have at least some underlying truth to them. He continued to develop his theory that matter was made up of a new layer of three fundamental particles: the up quark, the down quark, and the strange quark, with charge 2⁄3, –1⁄3, and –1⁄3, respectively. All other particles were made up of combinations of these quarks (and their antiparticles in the case of kaons and pions). The number of strange quarks in the makeup determined the strangeness of the particle.

Gell-Mann wasn’t the only one to play with the idea of pulling matter apart into these smaller particles. American physicist George Zweig also believed the patterns that had been observed hinted at a more fundamental layer of particles. He called them “aces” and he was even more convinced than Serber or Gell-Mann that these particles had a physical reality. His preprints explaining his ideas were dismissed as “complete rubbish” by the head of the theory group at CERN. Even Gell-Mann didn’t initially regard them as more than a mathematical model that created some coherent order in the pictures they were drawing. They were a mnemonic, not concrete reality. Gell-Mann dismissed Zweig’s belief in the physical reality of these particles: “The concrete quark model—that’s for blockheads.”

FROM FANTASY TO REALITY

That would all change when evidence emerged at the end of the 1960s from experiments conducted by physicists working at the Stanford Linear Accelerator Center in which protons were bombarded with electrons. Analysis of a proton’s charge revealed that it could be thought to have a size of 10–15 meters. The belief was that the proton would be uniformly distributed across this small region. But when electrons were fired at the proton blob, the researchers got a shock from the resulting scatter patterns. The proton, like the atom, turned out to be mostly empty space.

The scattering was, in fact, consistent with a proton that was made up of three smaller particles. Just as with Rutherford’s experiments on gold atoms, every now and again one of these electrons would score a direct hit with one of the three points and come shooting back toward the source of the electrons. The experiments seemed to confirm the idea that the proton was made up of three smaller particles. Although a quark has never been seen, the scattering of the electrons indicated, sure enough, that three smaller particles made up the proton.

It turns out the blockheads were right. The up, down, and strange quarks were not just a mathematical mnemonic; they were a physical reality. Over time it was discovered that these three quarks weren’t enough to cover all the new particles, and eventually we found ourselves with six quarks together with their antiparticles. In addition to the three Gell-Mann named, three more appeared on the scene: the charm quark, the top quark, and the bottom quark.

The discovery of quarks and their underlying symmetry is one of the most exciting discoveries of the twentieth century. Seeing these fundamental particles lining up in patterns that were already recognized in the mathematics of symmetry must have been so thrilling. If I could choose one discovery in physics I would love to have made, this one would rank pretty high. It must have been like an archeologist coming across a pattern that had previously been seen only in some other distant part of the world, and suddenly realizing there had to be a connection between the two cultures.

The weird thing is that this pyramid of triangles and hexagons giving rise to different representations of SU(3) goes on to infinity, implying that you could keep on gluing together more and more quarks to make more and more exotic particles. Announcements from the Large Hadron Collider in 2015 revealed exciting evidence for a five-quark particle. The researchers at CERN almost missed the particle, called a pentaquark, thinking it was just background noise. But when they tried to remove the noise they discovered a strong signal pointing toward this next layer in the symmetry tower. As one of the researchers working at CERN admitted, “We didn’t go out looking for a pentaquark. It’s a particle that found us.”

How much further can we push our understanding of mathematics to predict what else we might see in the LHC? There is an even bigger symmetrical object called SU(6) that would unite all six quarks—up, down, strange, charm, top, and bottom—into a fusion of fascinating particles. Instead of the two-dimensional pictures scientists have drawn combining particles together in families, you’d need five-dimensional pictures. Although it is possible to cook up some of these more exotic combinations of quarks, the beautiful mathematical symmetry breaks down as the differences in mass between the basic quarks is amplified. Indeed, the top quark is so unstable that it decays before it has time to bind to another quark. Why quarks have different masses seems to be a question that physicists don’t know the answer to—yet. The mathematics seems to suggest a much richer cocktail of particles than physical reality can actually sustain. Reality seems a pale shadow of what might be possible mathematically, but understanding that reality still holds many challenges.

I must admit that even with the mathematical toolkit I’ve spent years assembling, I’m still not sure I know what these quarks really are. I’ve sat at my desk poring over books on particle physics for months—light fare, such as Sudbury’s Quantum Mechanics and the Particles of Nature—and lecture notes downloaded for Oxford graduate courses and occasionally begun to despair a little. There is so much that I still don’t know: path integrals describing the futures of these particles, the inner workings of the Klein–Gordon equations, what exactly those Feynman diagrams that physicists so easily draw up on the board really mean. I look enviously at my son, who has started his degree in physics. He will have the time to steep himself in this world, to get to know these things as intimately as I know the area I chose to specialize in.

It is the same with my cello. As an adult I hanker to play those Bach suites now, not in ten years’ time. But just as it took years to learn the trumpet, so it will be a slow, gradual, sustained period of learning that will bring me to the point where I can play the suites.

As with the cello, I know that if I spend enough time in this world of particle physics I have some hope of understanding what my colleagues across the road in the physics department live and breathe daily. It frightens me to realize I don’t have time to know it all. But even those physicists whom I envy for the ease with which they play with our current state of knowledge recognize that ultimately they’ll never know for sure whether they know it all.

COWBOYS AND QUARKS

I arranged to meet one of the scientists responsible for discovering one of the last pieces in the quark jigsaw puzzle to see whether particle physicists think there may yet be even tinier pieces. Now a professor at Harvard, Melissa Franklin was part of the team responsible for detecting the top quark at Fermilab in Illinois. Contrary to popular perception, discovering a particle is not a eureka moment but a slow burn. But Franklin told me she preferred it that way: “If it’s just ‘boom,’ it would be a drag. You spend fifteen years building the thing and boom, in one minute it’s over? It would be terrible.” The team spent almost a full year gathering data before they felt confident enough in 1995 to confirm its discovery.

Franklin is definitely on the experimental rather than theoretical side of the physics divide. Happier with a power drill in her hand than a pencil, she helped to build the detector at Fermilab from the bottom up. We had both been invited to talk at the Rome Science Festival on the theme of the unknowable, so we agreed to meet in the lobby of our rather strange hotel, which seemed to be dedicated to the sport of polo. Given that Franklin strides around the department in cowboy boots, I thought she might feel more at home, but she ended up making an extremely dramatic entrance, crashing to the bottom of the stairs into the lobby. She dusted herself off and strode over as if nothing had happened.

I was keen to know if she thought quarks were the last layer or whether there might be more structure hiding beneath the particles she’d helped to discover.

“We’re down to 10–18 meters. The next seven or eight orders of magnitude are kind of hard to investigate,” she said. “But certainly a lot more could happen in there. It’s kind of strange that I could die before—especially if I keep falling down the stairs—I could die before we get any further.”

Did she think there might be fundamental limits to what we could know?

“There are definitely limits in my lifetime, but I’m not sure there are any other limits. In experimental physics, saying there’s no way we can do something is the perfect way to get someone to figure out how to do it. In my lifetime I’m never going to be able to measure something that decays in 10–22 seconds. I don’t think there’s any way. That’s not to say it’s provably unknowable.

“We couldn’t have imagined the laser or the atomic clock, right? I think all the limitations in physics are going to be atomic because all the things we do are with atoms. I know that sounds weird, but you need the atoms in your detector.”

It’s intriguing to consider how Einstein inferred the existence of atoms by looking at how they impacted things you could see, like pollen or coal dust. And today we know about quarks because of the way particles bounce off protons. I asked her if she thought there would be new ways to dig deeper.

“I’m sure those guys like Heisenberg and Bohr couldn’t have imagined what we can detect today. I guess the same must apply to our generation . . . although of course we’re much smarter,” she laughed.

I guess that is the problem each generation faces. How can we ever know what cunning new method might be developed to dig deeper into the fabric of the universe? Franklin wondered how much we were missing that was already there in the data coming out of the current generation of detectors.

“Many young people in my field don’t believe it’s possible to find anything new that wasn’t predicted by theorists. That’s sad. If you found something and it wasn’t predicted by theory, then you’ll probably think it’s wrong and you’ll dismiss it, thinking it’s a fluctuation. I worry that because of the way our experiments are constructed you have these triggers that trigger on certain things, but only things you’re looking for and not other things. I wonder what we’re missing.”

That was almost the fate of the pentaquark; it was nearly dismissed as noise. Franklin was intrigued to know whether, if I could press a button and know it all, I would do so. As I was putting out my hand to press her hypothetical button, selling my soul to Mephistopheles to know the proofs of all the theorems I’m working on, she stopped me in my tracks.

“I wouldn’t.”

“Why not?”

“Because it’s not fun that way. There are certain things, like if I could push a button and speak perfect Italian, I would do it. But not with science. I think it’s because you can’t really understand it that way. You have to struggle with it somehow. You have to actually try and measure things and struggle to understand things.”

I was intrigued. Wouldn’t she press the button if she could know there were more particles sitting underneath the quarks?

“If they just told me the method, then that would be great. But a lot of the reason we like doing science is coming up with the ideas in the first place. The struggle is more interesting.”

I think, in the end, Franklin likes making things. She likes driving forklift trucks and drilling concrete in the search for new particles, and wouldn’t want knowledge to come too easily.

“Experimentalists are a bit like cowboys in a way. Lasso that old thing over there and bring it over here. Don’t mind that boy over there sitting in the corner thinking about stuff.

“When I turn 60, I’m going to be less judgmental and more open minded,” she mused. “I’m going to stop being a cowboy . . . no, I don’t want to stop being a cowboy . . . I don’t know . . . it’s hard. Cowboys can be deep.”

And with that she strode out to a taxi and rode off into the Roman sunset, continuing the scientific quest to know what else is out there to tame.

THE CELLO OR THE TRUMPET?

Are the quarks that Franklin helped discover the final frontier, or might they one day divide into even smaller pieces, just as the atom broke into electrons, protons, and neutrons, which in turn broke into quarks?

Many physicists feel that current experimental evidence, combined with the mathematical theory that underpins these experiments, has given us the answer to the question of the true indivisible units of all matter. Just as the periodic table of 118 chemical elements could be reduced to different ways of assembling the three basic building blocks of the electron, proton, and neutron, the hundreds of new particles found in the cosmic-ray collisions could be reduced to a simple collection of ingredients. The wild menagerie of particles has been tamed. But how sure am I that the gates won’t open again to new customers? The truth is that physicists don’t know.

If you look at the symmetrical model underlying these particles, then the triangle corresponding to the quarks is the last indivisible layer. The mathematics of symmetry suggests that we’ve reached the end of the road. That triangle corresponding to the quarks is the indivisible layer that builds all the other layers. So the mathematics of symmetry tells me I’ve hit the indivisible. Maybe we are falling into the same trap that Gell-Mann did when he first dismissed quarks because they had fractional charges. And yet another feature of quarks and electrons provides some justification for the belief that they might not come apart: they don’t seem to occupy any space but behave as if they are concentrated at a single point.

In mathematics, geometry is made up of three-dimensional solids, two-dimensional planes, one-dimensional lines, and zero-dimensional points. The strange thing is that these were meant to be abstract concepts that didn’t have a physical reality in our three-dimensional universe. After all, what is a line? If you draw a line on a piece of paper and look at it under a microscope, you’ll see that the line actually has width. It isn’t really a line. In fact, it even has height, because the atoms that are sitting on the page are piling up to create a little ridge of graphite across the page.

Similarly, a point in space might be identified by its GPS coordinates, but you wouldn’t expect to find an object located solely at this point and nowhere else. You could never see it. Its dimensions would be zero. And yet an electron behaves in many ways as if it is concentrated in a single point in space, as do the quarks inside the proton and neutron. The manner in which electrons scatter off one another and off the quarks makes sense only in the context of a model in which these particles have no volume. Give them volume and the scattering would look different. If they truly are point particles, you wouldn’t expect them to come apart.

But what about the fact that electrons have mass? What is the density of an electron? It should be mass divided by volume. But what if the volume is zero? Divide by zero and the answer is infinite. Infinite? So is every electron actually creating a tiny black hole? We are firmly in the territory of the quantum world, because where a particle is located turns out not to be as easy a question to answer as one might expect, as we shall discover in the next Edge.

Have the discrete notes of my trumpet won out over the continuous glissando of the cello? It is very difficult to know. Atoms were regarded as indivisible because of the indivisible nature of the whole numbers that showed how they combine. And yet they eventually fell apart into the tiny pieces that make up our conception of the universe. Why shouldn’t I expect history to repeat itself with more surprises as I dig deeper and deeper? Why should there be a beginning, a first layer that made it all? It’s a classic problem of infinite regression that we shall meet over and over again. As the little old lady once told a scientist who mocked her theory that the universe was supported on the back of a turtle, “You’re very clever, young man, very clever, but it’s turtles all the way down!”

Even if electrons and quarks are particles concentrated at a single point in space, there is no reason why a point can’t actually be pulled apart to be made of two points. Or perhaps there are hidden dimensions we have yet to interact with. This is the suggestion of string theory. Point particles in string theory are actually believed to be one-dimensional strings vibrating at resonant frequencies, with different frequencies giving rise to different particles. Perhaps my cello does win out over the trumpet and the fundamental particles are really just vibrating strings.

Will we ever find ourselves at the point at which there are no new layers of reality to reveal? The current theory of the very small—quantum physics—proposes that there are limits to knowledge as I try to divide my dice into smaller and smaller units, that at some point I will run up against a barrier beyond which I cannot pass, as my next Edge reveals.