8

For in and out above, about, below

It is nothing but a Magic Shadow-Show

Play’d in a Box whose candle is the Sun

Round which we Phantom Figures come and go.

—Omar Khayyam, The Rubaiyat

I USED TO FANTASIZE about being able to look up at the night sky and point confidently at various stars and planets and declare: “That’s Betelgeuse” or “You see that bright spot there, that’s actually not a star but the planet Venus.” But one of my problems is that I have an extremely bad memory. If something’s random, like the stars scattered across the firmament, then without some logic to guide me, I find it very difficult to name much beyond the Plow. This is, of course, why we’ve created patterns like the Plow, or Orion the Hunter, to help us navigate these random spots of light.

But it turns out that I’m also not very physically suited to astronomy. My first attempt to take a deeper look into space was a trip to the telescope housed in Mill Hill in north London. But my wish to see to the edge of the universe was scuppered by the scourge of astronomers: clouds.

So next I tried to get above the clouds. This required more effort than jumping on the Northern Line to Mill Hill. I took a train to Switzerland, culminating in a beautiful alpine climb to the final stop at Jungfraujoch. From there a lift tunneled into the mountain took me to the mountain peak on which the Sphinx observatory sits, 3,571 meters above sea level.

Built in 1912, it looks like the villain’s lair from a James Bond movie. As the sun set over the snow and glaciers, I prepared myself for a wonderful evening of stargazing. Except my body had other ideas. I’d already been feeling quite dizzy and even nauseous. I hadn’t been able to eat much. As the first stars started to appear, I was hit by a crashing headache. Before long I was throwing up. When an elderly German couple said that I had all the symptoms of altitude sickness save one, it suddenly dawned on me that I’d never been this high before.

“And what’s the last symptom?”

“Death.”

It was then that I realized my dream of becoming an amateur astronomer wasn’t really worth it. I got the first train back to a sensible altitude and the symptoms disappeared. I just had to face it: I’m a Thames Valley boy born in London whose body was built to stare up at the stars from the comfort of a telescope closer to sea level. But observations made by some of those great telescopes that sit high on the mountains across the world have revealed a remarkable fact. At some point in the future, there won’t be so many stars for me to look at—they are disappearing over our cosmic horizon!

THE UNIVERSE THROUGH RED-TINTED SPECTACLES

When an ambulance drives by with its siren blaring, your ears experience the squashing up of sound waves as the ambulance approaches, which causes the wavelength to shorten, resulting in the siren sounding higher-pitched than when the ambulance passes you. As it pulls away, the sound waves are stretched out, resulting in a longer wavelength and lower pitch. This phenomenon is known as the Doppler effect.

The same thing happens to light. As a star speeds away from us, its light shifts toward the longer red wavelength. If it moves toward us, the light shifts toward the shorter blue wavelength. Having already discovered that our galaxy was not special but just one of many, Edwin Hubble turned his attention in 1929 to analyzing the light from these galaxies to see how they were moving relative to our own. To his surprise, the light from distant stars in the galaxies he observed was all shifted toward the red. Nothing seemed to be coming toward us. It was as if the other galaxies were fleeing from us. Even more interestingly, the farther the stars were from our own star, the more the wavelength shifted. Hubble couldn’t believe that the Earth was in such a special place in the universe. He soon realized there was a much better explanation: space is expanding in all directions simultaneously. Whatever your point of observation, it will appear that everything is moving away from you. The space between us and the stars is being stretched. The galaxies are being carried along by the expansion of space like leaves in the wind.

Although often credited to Hubble, an expanding universe was actually predicted by a Jesuit priest, Monsignor Georges Lemaître, two years earlier. Lemaître deduced that the universe must be expanding as a consequence of Einstein’s equations for gravitation. When Einstein heard about this theory, he dismissed it with the damning declaration: “Your calculations might be correct but your physics is atrocious.” Einstein was so confident that Lemaître was wrong that he ended up sticking something called the cosmological constant into his equations to try to force the universe to be static and thus scupper Lemaître’s prediction.

Lemaître didn’t help his cause by publishing his findings in an obscure Belgian journal. Once Hubble’s observations supported the idea of an expanding universe, Einstein changed his tune. Hubble's and Lemaître’s discoveries were the first indication that our universe isn’t static. Instead, space is always on the move.

It is the stretching of space that makes the wavelength of the incoming light longer. The farther the light has traveled, the more its wavelength will gradually have been stretched. We call this stretching redshifting because the visible light with the longest wavelength is red. So to say that light has been redshifted simply means that the wavelength has been stretched. The bigger the redshift, the more space has been stretched on the way and therefore the farther the original source of the light from Earth.

To explain why this stretching changes wavelengths of light, blow up a balloon and mark three points on it. One represents Earth, the other two points are distant stars. Draw two waves of light of a fixed wavelength between the stars and Earth. This is what the light looks like when it leaves the stars. By the time the light from the nearer star reaches Earth the balloon has expanded. If I blow it up a bit, the wavelength gets longer. It takes longer for the distant star’s light to reach Earth, so the universe has expanded a bit more. If I blow the balloon up even more, the wavelength gets longer again. So the greater the redshift, the farther the star is from Earth.

In the first balloon, the light leaves the stars with the same wavelength. In the second balloon, the universe has expanded and the light from the nearer star reaches Earth. The wavelength has gotten longer. In the third balloon, the universe has expanded further by the time the light arrives from the farther star. The wavelength has shifted even more toward the red.

This was a new way of measuring distance to far-flung stars. It has helped astronomers to identify stars that must now be thirty billion light years away from us. It may seem something of a paradox that we can see something thirty billion light years away when, as we shall soon see, the universe is only 13.8 billion years old, but remember that we are seeing the star in the past, when it was close enough that the light could reach us. It is only by analyzing the expansion mathematically that we can infer that today the star is at a point from which it would take its light thirty billion years to reach us.

THE ANT AND THE BAND

What does it mean to live in an expanding universe? If the universe is expanding, then perhaps some stars will always remain out of sight, since they are moving farther and farther away from us. But scientists have discovered that if the universe is expanding at a constant rate, even if that rate is faster than the speed of light, if we wait long enough, we’ll eventually see light from every star.

The best way to understand this is to consider an example that has a curiously counterintuitive outcome. Consider an ant (playing the role of a photon of light) sitting on the end of a rubber band (playing the role of space) that is stuck down at one end (playing the role of the Earth). The end where the ant starts plays the role of a far-distant galaxy.

Now pull the end of the rubber band at a constant speed. Suppose the rubber band starts with a length of one kilometer and every second it increases in length by one kilometer. The ant is moving at a much slower speed along the band, say, at one centimeter every second. At first glance, with the end flying off at a much faster rate, it appears as if the ant has no chance of reaching the other end, just as light from a galaxy far enough away seems to have no chance of reaching Earth if the space between them is expanding at a uniform rate.

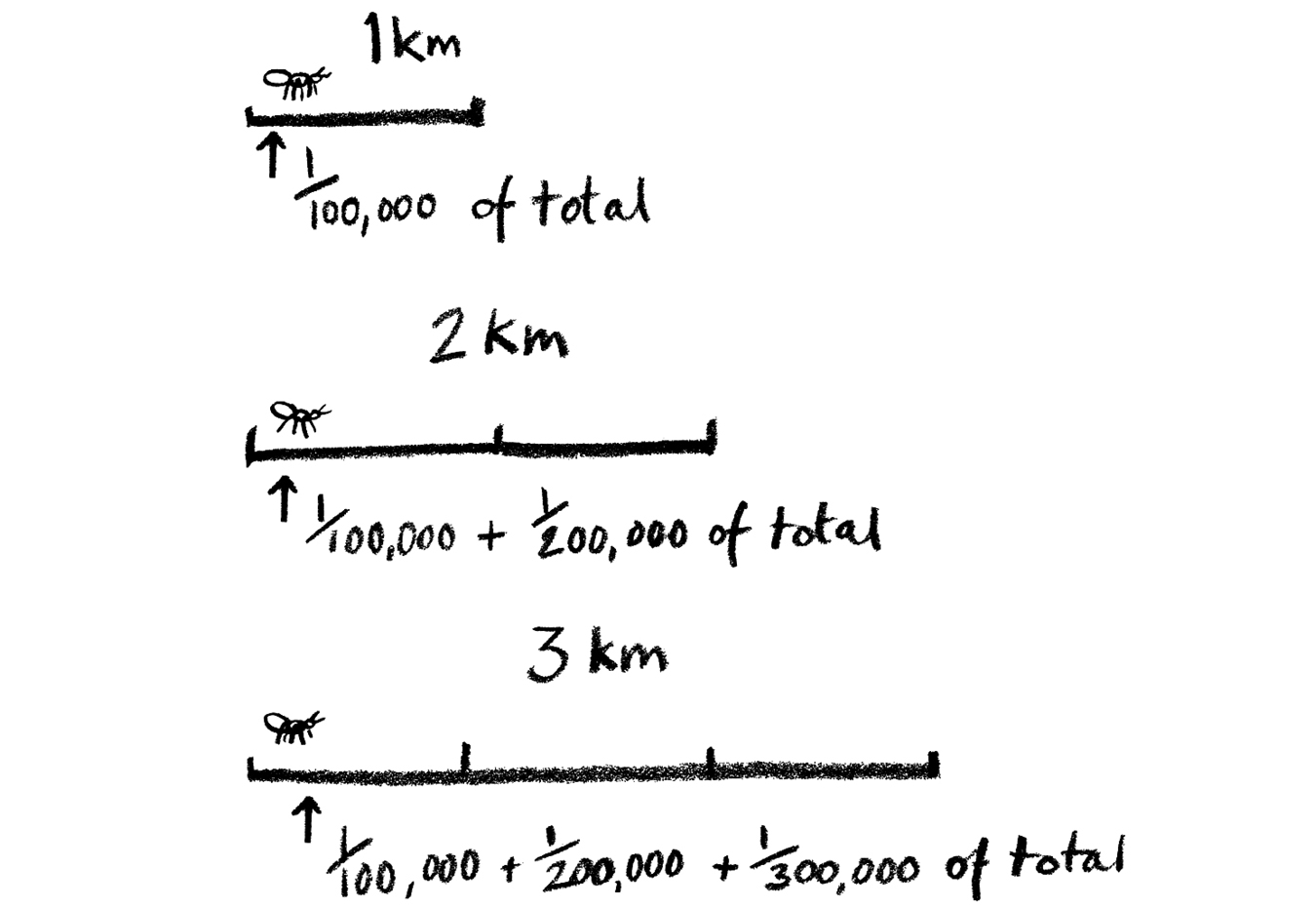
There are some subtleties here, so let me add a condition to help us get a grip on what is happening. The rubber band gets stretched only after each second, and it will be an instantaneous stretch. So after one second the ant has traveled one centimeter, which is 1/100,000 of the total distance. Then the band expands. The point to note is that although the distance that the ant needs to travel has increased, it has at least still covered 1/100,000 of the distance between the star and Earth, because the stretch has also helped push the ant on a little from its starting position.

Now the ant travels another centimeter. The rubber band is two kilometers long. So the ant has covered a further 1/200,000 of the total distance. The total proportion that the ant has now covered is 1/100,000 + 1/200,000 of this total distance. The band expands by another kilometer. The proportion hasn’t changed with the stretch. The band is now three kilometers long. The ant travels another centimeter. This is only 1/300,000 of the total distance. Every time the rubber band stretches, the proportion that the ant’s centimeter represents is going down. But hold on—here is the power of mathematics. After n seconds, the proportion of the band that the ant will have covered is

This is the harmonic series that the mathematician Oresme calculated many centuries ago and that I considered at the beginning of the last chapter. Oresme proved that this series will get arbitrarily large. So I can make n so large that the sum is bigger than 100,000. In that case, the proportion of the band that the ant has covered will be over one hundred percent. This means that the ant has arrived!

In this example I have the rubber band stretching at a uniform rate. This is pretty much how astronomers like Hubble thought space was behaving—perhaps even slowing down, given that gravity should have a decelerating effect. This implies that even if the universe is infinite, we should be able to see more and more of it if we just sit and wait—like a colony of ants crawling along the expanding rubber band of space.

Does this mean that in theory, if the universe is infinite, we should already be receiving light from all stars? Perhaps we can already see an infinite universe. The thing to remember, though, is that the farther away the star is, the further in the past we are looking at it. If we rewind our expanding universe far enough, we will find there were no stars at all.

REWINDING THE UNIVERSE

The discovery by Hubble and Lemaître of the expanding universe provided the first evidence for what scientists now call the Big Bang. If I reverse time, an expanding universe turns into a contracting universe. But keep contracting and the universe becomes so dense that the state of the universe changes rather dramatically. In fact, as Lemaître first realized, at some finite point in time this reversed expansion leads to a universe that is infinitely dense, a point he called the primeval atom or cosmic egg. This “singularity” is what scientists refer to as the Big Bang. Given that it is a point at which relativity and quantum physics must fuse into a coherent theory, there are still debates about how far we can rewind the universe before current models fail and new ideas are needed.

When I first heard about the Big Bang at school, I thought that if the universe started as a point then it had to be finite now. But with a bit of mathematics it is possible to show how an infinite universe can still start as a single point. This seems extraordinary. How can a point with no volume contain infinite space? To get an idea of how this works it is worth starting with an infinite space and working backward. Think of infinite space one second after the Big Bang. Take an arbitrary point as the center of this universe and consider all the points that are a distance R from this point. They all sit on the sphere of radius R.

Now I am going to rewind our universe backward to time zero. At time t = 1⁄2, the points on the sphere of radius R will contract to points on a sphere of radius 1⁄2R. At time t = 1⁄4, they’ve contracted further to sit on a sphere of radius 1⁄4R. As I keep halving the time in the direction of the Big Bang, this sphere is getting smaller and smaller, until at time t = 0 it becomes a point. But this is true of every sphere regardless of how big R is. So every point in my infinite space sits on some sphere of radius R and when rewound to t = 0 collapses to the point I chose. So in one second the mathematics gives me a way to suck infinite space into a single point with no volume. Shakespeare put it nicely when Hamlet declares, “I could be bounded in a nutshell and count myself a king of infinite space.”

Of course, we run into problems with this model if space and time are quantized. As I saw when I tried to keep halving my die, there may come a point when I can’t halve things. This is at the heart of the debate when quantum physics meets general relativity: trying to resolve what happens as we contract the universe to a point.

Many call this the beginning of our universe, and I shall return to the nature of what we mean by beginnings and time in the next Edge. But the Big Bang certainly has implications for just how far we may ultimately be able to see, because it means that the stars could not have existed for more than 13.8 billion years, which is the current estimate of how long ago the Big Bang occurred. It took some time after that before the first stars could form.

As you head out into space, you are heading back in time. Since there were no stars before 13.8 billion years ago, this means there is a sphere around us beyond which there will be nothing to see. The wonderful thing is that we are back to the model of the universe proposed by the ancient Greeks. There is a huge sphere with the Earth at its center, and photons from beyond that sphere have not had time to reach us yet. That sphere is getting larger as time passes, and the question of how much space is contained inside this expanding horizon will turn out to have an unexpected answer.

The farthest galaxy whose distance has been confirmed is one whose light has taken 13.1 billion years to reach us. That does not mean the galaxy is 13.1 billion light years away from us today, because the space between us has expanded over all those years. Calculations suggest that the galaxy is currently thirty billion light years away from Earth.

You might think we should be able to see light going back to the first moment after the Big Bang. But scientists now believe there was a moment when no light could travel through space because space was opaque. Photons just found themselves buffeted between one particle and the next. It was only 378,000 years after the Big Bang that the density of particles dropped sufficiently for the first photons to start their uninterrupted journey through space. This is when space suddenly had enough room for these photons to zip through the universe without running into something that might absorb them. These first visible photons of light make up what we call the cosmic microwave background radiation, and they represent the farthest that we can see into space. They are like a cosmic fossil telling us about the early universe.

Those first photons were only forty-two million light years away from Earth when they started their journey. Today, the distance has stretched to an estimated 45.7 billion light years. This is the edge of the visible universe, the cosmic horizon. But light isn’t everything.

Although light couldn’t make it through the plasma of space for 378,000 years after the Big Bang, neutrinos could. They are particles that don’t seem to be stopped by anything (well, hardly anything; every now and again they bump into stuff that allows us to detect their existence). You have trillions of neutrinos passing undetected through your body every second. So it’s possible that we could “see” a bit farther into space if we could detect the neutrinos that decoupled two seconds after the Big Bang.

There is a sphere surrounding the Earth that represents a horizon beyond which we cannot explore even with the most sophisticated of telescopes, because no information has had time to reach us. As time goes on, this cosmic horizon is growing, allowing us to see farther and farther into space. At least that’s what we thought for a long time, but a discovery in 1998 revealed the alarming fact that, rather than extending farther into space, our cosmic horizons are actually contracting. Although the cosmic horizon is growing at a constant rate, the underlying fabric of space itself isn’t just expanding, the expansion seems to be accelerating. As it does so, it is pushing things we can see out beyond our horizon, with devastating implications for what future generations can ever know.

THE STARS ARE GOING OUT

Some stars end their lives in a catastrophic explosion called a supernova. The luminosity is so intense that these supernovae can be seen over huge distances. When type 1a supernovae explode they all have the same luminosity, no matter where they are in the universe. When that is compared with the apparent brightness, we have a measure of how far away they are.

If the universe were expanding at a constant rate, then, given the distance of a supernova from Earth, you could predict the amount the wavelength of light should have been stretched by this constant expansion, or what we call its redshift. But when this theoretical redshift was checked against the recorded redshift of distant supernovae, astronomers got a shock. They didn’t match. It should have been much higher. For galaxies farther away, whose light allows us to look back in time, the rate of change of redshift was slower than that of closer galaxies. The only possible conclusion was that the expansion of space in the early universe was much slower, but then it started to accelerate, ripping space apart.

It seems that something dramatic happened about seven billion years ago. Up to this point, the universe’s expansion appeared to be slowing down, as one would expect as the gravitational force of the matter exerted a braking effect. But at this point, halfway through the current life span of the universe, the expansion rate changed character and started to increase, accelerating as if something had suddenly put its foot on the pedal. The fuel driving the acceleration is what scientists call dark energy.

It seems that in the first half of the universe’s existence, the density of matter was enough to exert a slowing gravitational pull, but as the universe expanded this density decreased to such a point that the underlying dark energy was strong enough to take over. Dark energy isn’t thought to be something whose density decreases with expansion. It is a property of space itself.

The sphere containing the visible universe is growing, which should mean that we can see even farther into space. Unfortunately, space is expanding so fast that stars that were previously within the sphere of the visible universe are being pushed beyond its edge. This suggests that in the future all galaxies other than our own will disappear from view and forever remain beyond the edge of our visible universe. Even though the sphere containing the visible universe is expanding, it will never expand fast enough to catch up with the galaxies as they are carried away by the acceleration of space.

Imagine if life had taken longer to evolve and humans had started doing astronomy only after all this interesting stuff had been pushed over the horizon. We would have an entirely different story of the evolution of the universe. It would look like the static universe that we believed to be our home before telescopes were able to pick out other galaxies. So what we can know depends on when we live.

Astronomy in the distant future won’t consist of going to the top of mountains and peering through telescopes like the one at the Sphinx observatory. Instead, it will consist of consulting books and journals full of the data recorded by previous generations of astronomers, before what they observed was pushed beyond our cosmic horizon. Perhaps future astronomy will be more suited to a Thames Valley boy like me who prefers low-lying libraries to high-altitude observatories. But it will take another 150 billion years before the other galaxies disappear over the cosmic horizon.

It is worth noting that we won’t ever lose the stars in our own galaxy. The local pull of gravity will keep the galaxy together. The expansion of space is not sufficient to pull the stars apart, but it raises the question of how much has already disappeared from view that might have told a different story.

If you are in a car and you want to accelerate, you need to put your foot on the pedal and produce energy by burning fuel. So where is the fuel or energy coming from that drives the acceleration of the universe, and won’t it run out eventually?

The answer is that we don’t know. Dark is used in cosmology to indicate that something doesn’t seem to interact with light or other forms of electromagnetic radiation. In other words, we can’t detect it. There are several conjectures as to what dark energy might be. One involves the cosmological constant that Einstein famously inserted into his equations to try to make the universe static. But now that constant is being used to push space apart. Usually we would think of energy spread out across space as being used up or thinning out as space expands. But this energy is now thought of as a property of space itself. More gets created as space grows. In any cubic meter of space it is constant. In other words, it has a fixed density. The acceleration is a runaway process that can’t be stopped. This doesn’t contradict the theory of the conservation of energy because dark energy is treated as a negative energy that is balanced by an increase in kinetic energy as space expands.

Information travels at the speed of light. With a static universe, this means that all information would reach us given enough time. With a universe expanding at a constant rate, my example of the ant on the expanding rubber band shows again that information traveling across an infinite universe would eventually reach us. But with an accelerating expansion, some things will never cover the intervening space quickly enough to counter the expansion. Using our current estimate for the cosmological constant we think might be responsible for this expansion, we believe that the sphere from beyond which we will not receive any information is currently eighteen billion light years in radius. As the space between the stars stretches, their light will stretch, too, and the more the light stretches, the longer the wavelength. Stars will seem to go out because the wavelength of light will be so elongated that we can no longer detect it.

It is amazing to think that cosmologists in the future may have no evidence that we live in an expanding universe. Future civilizations will perhaps return to the model of the universe held by the ancient world: our local galaxy surrounded by the void. We would look like an exceptional point in a universe of nothingness.

COSMIC FINGERPRINTS

If the universe is infinite, it seems very probable that its structure will preclude us from ever observing such a fact. And yet the universe beyond our visible horizon can still leave its fingerprints on the space we can see. If, on the other hand, the universe is finite, its shape will impose certain limitations on its behavior.

Think of the universe as a large resonating box like the body of my cello. The shape of the cello has been chosen because of the pleasing sound made by the frequencies that can vibrate within the box. What distinguishes a Stradivarius from a factory-made cello is partly the perfection of shape, which leads to a more beautiful sound. Can you deduce the shape of the box from the frequencies of the waves vibrating inside it? This is one of the intriguing problems that challenged mathematicians for some time. In a seminal paper, Mark Kac posed the question: “Can you hear the shape of a drum?” Only a square has the particular set of frequencies that are produced by a square. But in 1992, mathematicians Carolyn Gordon, David Well, and Scott Wolpert constructed two strange shapes whose resonant frequencies were identical, even though the underlying shapes differed.

In the mid-1990s, Jean-Pierre Luminet and his colleagues in France explored the cosmic microwave background radiation to see what waves were left over from the Big Bang. They believed waves with long wavelengths seemed to be missing from the spectrum. Was space not big enough to support them? Alas, more refined data from the Planck spacecraft released in 2013 has revealed that there is no such evidence of missing wavelengths that would have hinted at a finite universe. So the jury is still out. And therein lies the real dilemma—if the universe is finite, we could conceivably someday know it, but if it is infinite, we will forever be left in a state of epistemological unease.

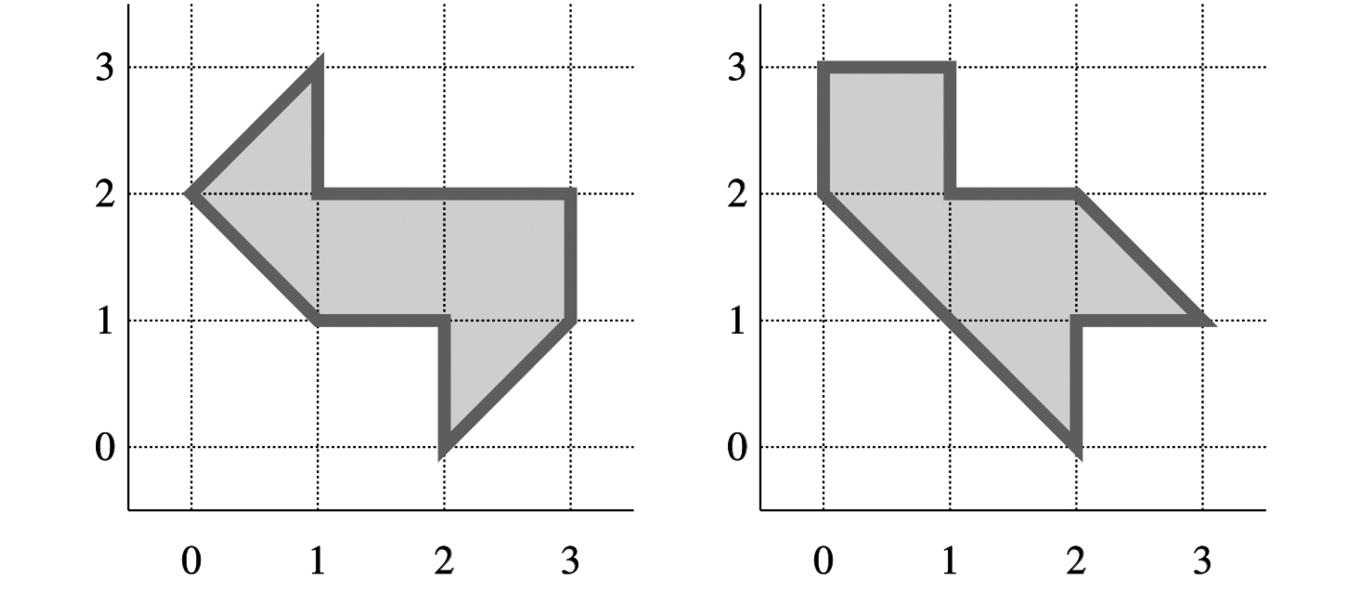
Two drums with the same resonant frequencies

Although the waves detected in the microwave background radiation can’t tell us whether the universe is finite, they may allow us to estimate its minimum size. For starters, they give us a chance to sneak a peek beyond our cosmic horizon. As Soviet scientists Leonid Grishchuk and Yakov Zel’dovich explained in a paper in 1978, certain waves can resonate only if the universe is big enough. Patricía Castro, Marian Douspis, and Pedro Ferreira have used the resonances that we can detect to propose that the universe is at least 3,900 times bigger than the space we can see.

Another way we may be able to deduce things about space beyond the edge of our visible universe is to witness events that can only be explained by influences outside our cosmic horizon. For example, something large beyond our cosmic horizon might be pulling on the galaxies we can see, causing an unusual drift in certain regions of the night sky. Although we might not be able to see this large thing, we can still experience its effect on the things we can see. What we can know is not limited to what we can see. This is, in fact, how we know about dark matter. The gravitational behavior of the things we see makes sense only if there is more stuff out there. It is also how we discovered Neptune. Although we eventually saw Neptune with our eyes, its existence was initially predicted on the basis of the effect it was having on the planets around it.

As long as humans have been looking out at the night sky, from one generation to the next we’ve constantly found ourselves adjusting our sense of scale. At first it appeared that the Earth was the center of it all. Then we had to readjust our position in the cosmos when we realized that the sun was at the center, with the Earth just one of many planets orbiting the sun. Then we realized that all those stars out there might have their own planets and that our sun was tucked away at the edge of a galaxy of stars. And then we had to rethink our place in the universe once more as we came to terms with the fact that there were billions of other galaxies out there in space.

Discoveries made in my lifetime—since I’d come to terms with my place in the universe—have forced me to expand my horizons once again. Just as previous generations recognized that our planet was actually one of many, so it appears we have to face the possibility that our universe is simply one of many universes. The first inkling of these other universes was provided by a rather curious enigma encoded in the very first photons that zipped through our own universe.

THE MULTIVERSE

There is something curious about the cosmic microwave background radiation. Why is it so uniform? The photons that we are picking up in our detectors all have a temperature of 2.725 degrees above absolute zero. When they set off on their journey some 370,000 years after the Big Bang, they were much hotter—around three thousand degrees, the temperature at which electrons and nuclei amalgamate to become atoms. As space expanded, the photons cooled off, which means that their energy gradually decreased, until today it is so low that we find them in the microwave region of the electromagnetic spectrum.

But why do all photons have very nearly the same temperature? If two objects of different temperatures come into contact, then over time they will transfer energy from one to the other until their temperatures equal out. This may seem like the obvious explanation, except that there is an important word in that sentence: contact. Einstein’s theory of relativity implies that information cannot travel faster than the speed of light. For one photon to communicate its temperature to another photon it needs to be close for long enough for this information to travel between them. This means that to reach a common temperature, opposite sides of the universe must have been much closer to each other much longer than our model of an expanding universe had suggested.

In the early 1980s, American cosmologist Alan Guth came up with a potential solution. He posited that in the early stages of the universe’s existence, space didn’t expand quickly. It was a slow start, allowing its photons to achieve a uniform temperature. Then space went through an exceedingly rapid expansion in a period that is now called inflation. An antigravity field confusingly called the inflaton is conjectured to have pushed space apart at an exponential rate. The rapid inflation didn’t last for long: some 10–36 seconds, according to the current model. That’s a billionth of a billionth of a billionth of a billionth of a second. Yet in that time, space is thought to have expanded by a factor of 1078. It’s as if a buildup in pressure had suddenly been released, after which the universe settled down into the more sedate expansion we have picked up since.

This model helps explain why the universe appears flat and essentially homogeneous. The large variations we see, like galaxies here but empty space there, are actually the product of very small quantum fluctuations in the small bit of space that were blown up by this massive inflation. The inflation also explains why the universe appears so flat. It would have virtually flattened out any identifiable curvature that had been present in the early universe.

The mathematics developed to explain this inflation, by Andrei Linde at Stanford and Alexander Vilenkin at Tufts, makes an extraordinary prediction. It implies that space could be inflating in other regions of space. Quantum fluctuations across space cause the inflaton field to pop in certain places, creating vast universes. In other words, there may be other universes out there like ours, making space look like Swiss cheese, with the holes in the cheese corresponding to different universes.

Can we ever know whether this description of the universe is true? Are we just coming up with internally consistent stories that could be true but are untestable? Even in our own universe there seems to be a limit to how far we can see. So how can we hope to know whether these other universes are real or just the fantasy of theoretical physicists?

Scientists hoping to prove the existence of these other universes have focused on the possibility that they might interact with our universe in such a way as to leave some sort of imprint. Could the cosmic microwave background radiation provide evidence that our universe collided with other universes during its formation? There has been some speculation that temperature differences in the map of the early universe could be a result of such collisions, but, as a member of the team at University College London investigating this possibility admits, “One of many dilemmas facing physicists is that humans are very good at cherry-picking patterns in the data that may just be coincidence.” It is devilishly complicated, but not a hopeless quest. Discovering evidence for neighboring universes is not a priori something beyond our reach. The challenge is to find ways in which these other universes could have influenced what we see within our cosmic horizon.

DIALING UP DIFFERENT UNIVERSES

One of the intriguing consequences of these potentially unknowable universes is that they provide us with a way to answer one of the principal questions with which many believers challenge those who don’t believe in a God. The possibility of the multiverse offers the best rationalization we have so far for the troubling feeling that our own local universe must have been designed.

I’m not talking about the illusion that only a supernatural designer could explain the complexity of life. Thanks to Darwin’s theory of evolution, we don’t need a designer. But what we lack is a good explanation for the constants of nature—the twenty or so numbers like the mass of an electron, the gravitational constant, the speed of light, the charge of a proton—that had to be so perfectly fine-tuned to get life up and running. Although we have a mechanism that explains biology, we don’t have a similar way to explain physics.

There seems to be no clear rationale for why these constants assume the values they do. Why couldn’t they be dialed to other values? What is particularly striking is how sensitive the possibility of life in our universe is to a small change in these constants. For example, if the constant that controls the way the electromagnetic field behaves is changed by four percent, then fusion in stars could not produce carbon—any life that could exist in such a universe would have to be based on other atoms. Some of the other constants turn out to be similarly sensitive to small tweaks. Change the cosmological constant in the 123rd decimal place and suddenly it’s impossible to have a habitable galaxy.

The multiple universes beyond our cosmic horizon could hold the solution to this dilemma. In the multiverse model there are lots of different universes, and in each of these universes the fundamental constants could be randomly assigned. In most cases, a universe wouldn’t really have much going on because the constants aren’t set favorably for action. But in a few, the constants are in the sweet spot for atoms to form out of the soup of electrons and quarks in a way that eventually leads to life. Of course, for us to be around to observe this universe, we have to be in one of these special universes. This is known as the anthropic view.

I think most scientists hope for a more satisfying answer to why our universe is the way it is. They’d like to be able to show that these constants aren’t really random, that things had to be the way they are. Relying on multiverses feels like a bit of a cop-out. But perhaps I have to bite the bullet and accept the multiverse model. The Earth may just be a random planet that turns out to be in the sweet spot for life. I’m not going to be able to come up with a reason why it had to be there. Lots of planets failed to be in the right spot. It’s just chance that our planet fits the bill. Perhaps our universe is the same, one of many different universes that just happens to be in the sweet spot for life.

My hope is that we can explain why the universe has to be the way it is without recourse to the idea of the multiverse. That is what most scientists would prefer. Some suggest that there is an explanation—a transcendental intelligence that fine-tuned the whole thing. But that feels like even more of a cop-out. The multiverse theory at least has that sense of economy we are after in a good theory. The explanation terminates and does not require further explanation. The addition of these other universes is just more of the same with variations, and once you accept all these universes you get a complete solution to the fine-tuning problem. A designer who fine-tunes the constants raises as many questions as it answers.

A good scientific theory should make sense of how everything is put together, and you shouldn’t need to introduce too many extra characters into the story to get the narrative we experience. There is a simplicity and naturalness about the multiverse theory that makes it a strong candidate theory. The physics of inflation provides a possible mechanism for producing these other universes, so it isn’t just a wild hypothesis. But we need to take care when using the qualities of simplicity and economy to judge the possible truth of a theory.

If I asked you to name the next number in the sequence 1, 2, 4, 8, 16, . . . , the obvious answer would be 32. To guess that doubling is the key to this sequence would be the majority view. But what would you say to the person who announces that 31 is the next number? That person would probably be laughed at. But once you know that these numbers could describe the number of ways you can divide a circle, both 31 and 32 become legitimate responses. So then you may ask for more experimental data to help you decide which is the best explanation.

Why 31 Is the Next Number . . .

Place n dots on a circle and then draw lines connecting each dot to the other dots. How many regions have you divided the circle into? The maximum number of regions you get starting with one dot follows the following sequence: 1, 2, 4, 8, 16, and then at six dots there is a surprise—you get a maximum of thirty-one regions.

The interesting point is that, however much data you uncover, I can give you an equation that will provide a coherent reason for why any number might legitimately come up next. So, given a finite amount of data, it seems we can never really know what the explanation is for that data unless we can get another bit of data against which to test our equation. This is the model of science that the philosopher Karl Popper proposed: a theory can only be falsified, never proved.

In judging a good theory, scientists often apply some measure of simplicity, an Occam’s razor measure that favors one equation over another. The simplicity of the equation—that is, the less you have to put in to get an answer out—is generally significant when deciding which explanation to favor. That’s why most would choose doubling as the obvious explanation for the sequence of numbers, rather than the quartic polynomial that gives us 31.

So, when we are faced with two competing theories and there is no way of telling which one is right, it does seem to be the case that we favor the simplest theory. This is captured by the idea of something philosophers call “inference to the best explanation,” or the theory of abduction. But there is no reason why simplicity should guarantee truth.

Our association of beauty with truth comes from our being evolutionarily programmed to respond with a shot of dopamine when we think we’ve struck on an idea that helps us to navigate our environment. We call things beautiful because of our body’s response to something that will be advantageous to our evolutionary survival.

What happens when alternative stories are proposed? How do you deal with people who believe the universe is 5,775 years old? You show them the fossil record and they counter that the universe was created old. They construct for themselves a narrative that is logical and self-consistent but to my mind highly unlikely. It is hard to argue with someone who posits a theory that is immune to testing.

Increasingly we are being pushed toward scientific narratives for the evolution of the universe that may turn out to be untestable. If you come up with a theory that predicts new particles but the theory doesn’t pin down at what energy these particles can be detected, no amount of evidence will convince those who believe in this new theory that they are wrong. They will always retort that the hypothetical particles exist in the region that you haven’t been able to test yet.

Some have argued that the current untestability of the multiverse theory means that it is as fanciful as proposing that a supernatural designer fine-tuned the whole thing. Although at the moment there is no way of testing the multiverse theory, there is no a priori reason why it will always remain untestable. The same applies to string theory, which is often shot down as a scientific theory because it fails to make predictions that can be tested. But that is no justification for throwing it out yet, as there is no reason to believe that it will always remain untestable.

The multiverse theory, although potentially untestable, does come with a mechanism, inflation, for how these multiverses arise. And we do at least have evidence for one of these multiverses: our own universe. One of the criteria for a scientific theory is that it should provide explanations based on things that are natural rather than supernatural. If you are going to posit a new thing like “dark energy” or “gravity,” you need to embed it in the natural world. How can you do that? You show how its behavior affects the rest of what we see and experience.

Another criterion for good science is that you can do experiments to test your theory. One of the problems with cosmology is that it is a one-time experiment. It is very difficult to run another Big Bang and to see what happens. That said, you can test the conditions of the Big Bang on a small scale on Earth to get a sense of the physics of the larger cosmological event. But it’s difficult to see how you could test whether other physical theories with different fundamental constants, or even different physics, could emerge from different moments of creation.

Since experiments are out, one of the central tenets of cosmology is the concept of homogeneity. You have to work under the assumption that what happens in our local bit of the universe is representative of its overall structure. Without this assumption, anything goes. We assume that the way space curves near us is true universally, but this need not be the case, just as someone living on the flat part of a hemisphere-shaped planet will think the whole planet is flat until they reach the point where curvature changes.

Without the assumption of homogeneity, how can we preclude the possibility of something outrageously different going on beyond our horizon? Perhaps someone has downloaded our universe from a website and glued it together like my celestial sphere. Perhaps we are just the dollhouse of some supernatural being—supernatural in the sense that it exists outside our universe. If this supernatural being never plays with the dollhouse, it is unclear that we could ever know about it. But if it truly has no influence, then why imagine that it exists? Why do we need to let our imaginations run riot? If this supernatural being plays with its dollhouse, then we are up for testing its impact and it is potentially knowable.

IS THERE ANYONE OUT THERE?

It is striking how often cosmology and religion have intersected throughout history. The question of what might lie beyond the edge of the universe has always intrigued scientists and theologians alike. For the medieval philosopher Oresme, this was where God was hiding. Most religions include a creation myth for the cosmos. For the Australian Aborigines everything spewed forth from the belly of the Rainbow Serpent. For scientists it’s the Big Bang. Galileo ran into trouble with the Catholic Church because he challenged its conception of our place in the cosmos. Yet it was a Jesuit priest, Lemaître, who came up with science’s current story of how our cosmos emerged from the Big Bang.

Even in our current era, cosmology and religion are sometimes controversially intersecting. In 1972, Sir John Templeton, an American-born British entrepreneur, introduced a prize (given in his name) to reward “progress in religion.” It has evolved to recognize “progress toward research or discoveries about spiritual realities.” It is a big-money prize, currently standing at £1,100,000. Templeton stipulated that the prize should exceed the Nobel Prizes, which he felt had unjustly ignored the spiritual dimension.

The prize has been awarded to some obvious people. The first Templeton Prize went to Mother Teresa. Subsequent prizes have rewarded priests, evangelists, rabbis, and the Dalai Lama. But in recent years a growing number of scientists have joined their ranks, and invariably it’s scientists researching cosmology and big questions about the universe who have been honored.

A number of leading scientists have been critical of those who have accepted the prize, believing that it endorses a spiritual approach to scientific questions. My predecessor Richard Dawkins, one of those critics, declared that the prize was usually given “to a scientist who is prepared to say something nice about religion.” Physicist Sean Carrol outlined his reasons for refusing funding from the Templeton Foundation. “It’s not a matter of ethical compromise,” he wrote. “It’s simply a matter of sending the wrong message. Anytime respectable scientists take money from Templeton, they lend their respectability—even if only implicitly—to the idea that science and religion are just different paths to the same ultimate truth.”

I was keen to talk to a cosmologist who had accepted the prize and approached Professor John Barrow, based in the Department of Applied Mathematics and Theoretical Physics at the University of Cambridge, who received the Templeton Prize in 2006. “Most of the fundamental questions in cosmology are unanswerable,” he immediately wrote back in response to my e-mail. “In fact, I will talk about some of them in a lecture I’m giving this Saturday.”

Perfect. Here was a chance to hear what cosmologists believe are the great unknowns. Sitting in the front row of the lecture hall, I waited impatiently for him to begin. As Barrow went from one question to the next, accompanied by the obligatory pretty pictures with which astronomers pepper their presentations, he proceeded to confirm all the fears I’ve been accumulating about how little we can know about our universe.

The Big Bang: “At a finite time in the past the universe seemed to have a beginning—a time when the density was infinite and the temperature was infinite. We don’t know if that beginning was real.”

The size of the universe: “There is no doubt a lot of universe beyond our horizon, but we haven’t seen it, and almost all of it we will never see. So when people ask whether the universe had a beginning, or is it finite or infinite, we can never answer questions like those about the entire universe.”

When I met up with Barrow after the lecture and challenged him about the Templeton Prize, he explained to me why he thought the Templeton Foundation was funding and rewarding cosmologists. “Sir John Templeton liked science because there was progress. He believed cosmology was tackling deep and important questions that everyone ought to know about whatever they were doing, whether it be philosophy or religion or theology. You couldn’t study those subjects while ignoring what was going on in the rest of science.”

Barrow believes the science–religion debate needs to be much more nuanced. “One of the lessons to be learned for people who are interested in the science–religion interaction is that you have to say which science you mean because the interaction is very different.

“Cosmology and fundamental physics bring you into contact with these big questions that you know you’re not going to answer. You’re used to uncertainty, to not knowing, and, to some extent, seeing why you’re not knowing. People in lab physics or biology, like Dawkins, they’re not used to that kind of situation. They think every problem is solvable by grinding it down.”

Not that Barrow was belittling what they do. “People always think that because you’re studying the universe this must be the hardest problem. Not at all. Understanding the brain, for example, is a much harder subject. It’s much more complicated. In cosmology things happen very slowly, there are nice approximations for understanding. You can pick a simple symmetrical solution and then iterate away. You can’t do that with human society. There’s no simple model.”

Barrow believes that the science he is engaged in has a markedly different quality. “In fundamental physics and cosmology you know there are problems that you’re not going to solve. Why are there laws of nature at all? The question of the number of dimensions of space and time. Whether there is a multiverse. Was there an initial singularity? Is the universe infinite? You can think of loads of questions that you’re not going to answer. This creates a different complexion.”

Barrow received the Templeton Prize for his work highlighting the intrinsic limitations of scientific inquiry. There is a growing tendency to think that science will ultimately be able to fill all the gaps, and Barrow is keen to rein in this faith in the all-knowing power of science. He is a big believer in the Copernican principle that we are not at the center of things and that the universe does not revolve around the human race.

“The universe is not constructed for our convenience. It’s not an exercise in the philosophy of science. It’s too bad if we can’t find these things out. In fact, I’d be very suspicious if all these fundamental questions happened to be answerable by what we’re doing. I would regard that as anti-Copernican. So I regard the fact that we can’t solve certain problems, or we can’t get the data we need, as a Copernican aspect of things.”

BLACK SWANS, BIASES, AND THE BACK OF THE BOOK

Barrow believes we must recognize that we have an extraordinarily biased view of our universe. “Most astronomy is based on observing things that shine in the dark: stars in distant galaxies, so-called luminous matter. Only five percent of the universe is composed of ordinary material that composes us and the luminous stars. Luminous material is rather biased. Luminous material tells you about places in the universe where the density became so high that nuclear reactions could ignite and produce luminosity.”

In some ways, this applies to the whole of science. Our view of the universe is biased toward the bits that have impact on our senses. Anything that doesn’t isn’t going to get noticed.

“If you lived on a planet that was covered in cloud all the time—planet Manchester, say—then there would be no astronomy. On the other hand, you might learn an awful lot about meteorology.”

In Barrow’s view, cosmology has a very different quality to other sciences, and this may be key to its close relationship with theology. “If you’re a scientist you’re used to carrying out experiments, testing theories. You can’t experiment on the universe. You just have to take it as it is.”

Many modern scientists have signed up to Karl Popper’s conception of the limits of knowledge—that because you can never actually prove that a scientific theory is correct, the best you can do is to try to falsify it. All swans are white. You can never prove that. The best you can do is to falsify it by discovering a black swan. In Popper’s book, anything that can’t potentially be falsified is therefore unscientific. So if you can’t do experiments in cosmology, are large swathes of it unscientific? Barrow wasn’t going to give in too quickly.

“Popper’s philosophy of science is incredibly naive. It doesn’t really work in astronomy, because when you make your observations you don’t know whether they have been made correctly. So your prediction might have been falsified because something has been done wrong in the experiment. Or, more likely, there is some bias in the way the evidence has been gained.”

Black swans seem pretty damning for a theory that says all swans are white, but in other more complex settings, it might be much less clear whether the theory is at fault, or the evidence. Perhaps the swan rolled in coal dust before you observed it.

Barrow believes that cosmology could have its own black-swan moment. “The key data point in all these ultimate questions that could really change things is making contact with some well-evolved extraterrestrial civilization that has evolved independently and knowing how they have come to think about some of these questions. Have they found the same bits of math useful? Have they done physics in the same way? Do they define fundamental constants in ways that we could make sense of? What do they think about these ultimate questions? Now this would be an unsurpassably important data point and is the most important reason to make contact with extraterrestrials.”

Given the tantalizing possibility that this advanced civilization might have come up with answers to some of our big questions, I thought Barrow would be excited by the possibility of contact. But I got a surprise.

“The scientific content I think will be a disaster. If we made contact with a very advanced civilization that had answered all the questions we had ever posed, the game would be over for us. There would be no motivation for us to do science. It would be like looking at the back of the book and finding all the answers.”

You wouldn’t want to do that?

“I think it would be a disaster.”

Just as particle physicist Melissa Franklin didn’t want to press the button that would give her complete knowledge, so Barrow was averse to looking up the answers in the back of the book. Unlike Franklin, Barrow is convinced that there are questions that even the most advanced civilization will never be able to answer. Those pages, to his mind, will forever remain blank.

“The bad news is that cosmology has unknowable unknowns: things that we are never going to know even though we suspect we might know of their existence.”

MAKING CHOICES

Many would argue that you should remain agnostic in the light of an unknowable question, so I was intrigued to know Barrow’s stance on the question of God. Was he agnostic? Atheist?

“Christian, in fact.”

That was a surprise. I have heard Barrow talk many times, and have read many of his books, but unlike Polkinghorne, he does not wear his beliefs on his sleeve (or around his neck). But I guess I also have made a choice. I don’t believe that the only logical response to an unanswerable question is to remain on the fence.

Our response to an unknowable question can have implications for how we conduct ourselves. Take, for example, the question of whether the universe is infinite. That may well be a question that we will never be able to answer. So should we just remain agnostic on the subject?

There is an argument that we would be wise to take out Pascal’s wager on this one. If the universe is infinite, you’re (probably) never going to know. But if the universe is finite, it’s possible that you could know this. So isn’t the better strategy to choose to believe that the universe is finite? In the end, if the universe is infinite you can never be proved wrong, but if it’s finite you could be proved right.

But what if an infinite universe offers a more exciting framework within which to live your life? An infinite universe has some interesting implications. One of these is that there could be infinitely many copies of you across the universe reading this book. The psychological impact of this conclusion might have a dramatic effect on the way you live your life.

Why There Could Be Infinitely Many Copies of You Reading This Book

This hinges on a couple of assumptions. The first comes from quantum physics; namely, that everything in the universe is quantized. This means that in a finite region of space there are only finitely many points and they can take only a finite number of different values.

A simplified version of this universe looks like an infinite checkerboard on which each square can only be black or white. Take a region of this checkerboard, which is meant to represent the complexity of life, including you reading this book. Suppose, for example, that it is a 10 x 10 region with a particular pattern of black and white squares.

One model of the entire infinite universe is that outside this 10 x 10 region everything else is colored black. Rather like the void. So we need another assumption: that it is equally probable that any of the possible patterns can occur. No pattern is favored over any other. Since there are only finitely many possible patterns and infinitely many 10 x 10 cells across this universe, if our pattern occurred only finitely many times then there must be another pattern that occurs infinitely often and therefore is infinitely more likely, which contradicts our second assumption. That means our pattern must be repeated infinitely across the checkerboard universe.

I think this is why I reject Pascal’s original wager on the question of the existence of God (in the conventional sense of a supernatural intelligence that created the universe) and choose to declare myself an atheist. Ultimately it affects the way I conduct my life. I’m not denying that it is a question I may never know the answer to, but to admit such leaps of the imagination would open up too many other wild possibilities. It goes against my natural predisposition to argue for the best explanation. Believing in multiverses may not be the most satisfying thing, but it is to my mind a better—or simpler—explanation.

CAN WE REALLY EVER KNOW WE WON’T KNOW?

After leaving Barrow in his office, I was rather downcast. I know I was on the lookout for things we cannot know, but I was beginning to doubt whether we could actually ever know anything. On my way back home, lines in one of Barrow’s books struck a chord: “The idea of the impossible rings alarm bells in the minds of many. To some, any suggestion that there might be limits to the scope of human understanding of the Universe or to scientific progress is a dangerous meme that undermines confidence in the scientific enterprise.”

Looking back at the Edges we’ve visited so far, nothing seems quite so unanswerable as the question of whether the universe is infinite. Chaos theory told me that the future was unknowable, but I can just wait until it becomes the present and then I’ll know. As I slice my die, I might actually hit a point at which space is quantized, so it’s possible that there are only finitely many steps inside my die before I hit the indivisible. It’s true that it might be almost impossible to navigate this parsing into even smaller pieces, but it isn’t a challenge that is a priori unsolvable. And Heisenberg’s uncertainty principle does not so much challenge us to give an answer as to consider whether the questions we are asking are well posed. It’s not that we can’t know position and momentum simultaneously; the revelation is that it is not a question it makes sense to ask.

But the question of an infinite universe does not seem ill posed. The universe is either infinite or not. If it is infinite, it is a real challenge to think of how we could ever know this, given what we’ve discovered about the cosmic horizon.

Then I had a revelation. Perhaps the question of an infinite universe is not as unknowable as one might think. Might there not be a more indirect way to reach a conclusion? The answer might lie in my own field of expertise. Mathematics has been a very powerful telescope through which to view the universe. What if the current laws of physics lead to a mathematical contradiction under the assumption that the universe is finite? That would force us to conclude that the universe must be infinite, or that our laws of physics are at fault. This is, after all, how we discovered irrational numbers.

This is in fact the power of mathematics: to use our finite brains to know the infinite. The Pythagoreans showed that the length across the diagonal of a unit square is given by a number that can’t be written as a simple ratio of whole numbers. The only way this length can be expressed is by a decimal expansion that is infinite and nonrepeating. Perhaps an infinite universe will be susceptible to a proof of existence by the same tools that helped us discover irrational numbers—a proof by contradiction.

Perhaps the real lesson is that “what we cannot know” is something we can never know because it is so hard to preclude the possibility that new ideas might pull the unknowns into the known. Although the universe that I will ever be able to see or explore is as finite as the paper model that sits on my desk, perhaps the message is that we should not give in too early to the lure of the great unknown. The mathematical telescopes of the mind may one day allow us to break through the unknown and discover that our sphere really does sit in an infinite expanse of space.