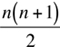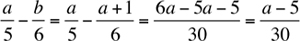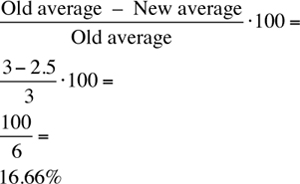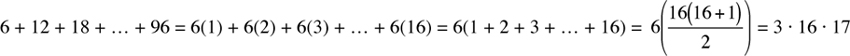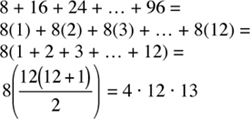Number Theory
This broad category is a popular source for GRE questions. At first, students often struggle with these problems since they have forgotten many of the basic properties of arithmetic. So, before we begin solving these problems, let’s review some of these basic properties.
 “The remainder is r when p is divided by k” means p = kq + r, the integer q is called the quotient. For instance, “The remainder is 1 when 7 is divided by 3” means 7 = 3 · 2 + 1. Dividing both sides of p = kq + r by k gives the following alternative form p/k = q + r/k.
“The remainder is r when p is divided by k” means p = kq + r, the integer q is called the quotient. For instance, “The remainder is 1 when 7 is divided by 3” means 7 = 3 · 2 + 1. Dividing both sides of p = kq + r by k gives the following alternative form p/k = q + r/k.
Example 1: The remainder is 57 when a number is divided by 10, 000. What is the remainder when the same number is divided by 1, 000?
(A) 5
(B) 7
(C) 43
(D) 57
(E) 570
Since the remainder is 57 when the number is divided by 10, 000, the number can be expressed as 10, 000n + 57, where n is an integer. Rewriting 10, 000 as 1, 000(10) yields
1,000(10)n + 57 =
1,000(10n) + 57 =
Now, since n is an integer, 10n is an integer. Letting 10n = q, we get
1,000q + 57 =
Hence, the remainder is still 57 (by the p = kq + r form) when the number is divided by 1, 000. The answer is (D).
Method II (Alternative form)
Since the remainder is 57 when the number is divided by 10, 000, the number can be expressed as 10, 000n + 57. Dividing this number by 1, 000 yields
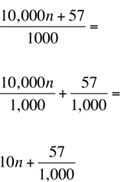
Hence, the remainder is 57 (by the alternative form p/k = q + r/k), and the answer is (D).
 A number n is even if the remainder is zero when n is divided by 2: n = 2z + 0, or n = 2z.
A number n is even if the remainder is zero when n is divided by 2: n = 2z + 0, or n = 2z.
 A number n is odd if the remainder is one when n is divided by 2: n = 2z + 1.
A number n is odd if the remainder is one when n is divided by 2: n = 2z + 1.
 The following properties for odd and even numbers are very useful—you should memorize them:
The following properties for odd and even numbers are very useful—you should memorize them:
even × even = even
odd × odd = odd
even × odd = even
even + even = even
odd + odd – even
even + odd – odd
Example 2: If n is a positive integer and (n + 1)(n + 3) is odd, then (n + 2)(n + 4) must be a multiple of which one of the following?
(A) 3
(B) 5
(C) 6
(D) 8
(E) 16
(n + 1)(n + 3) is odd only when both (n + 1) and (n + 3) are odd. This is possible only when n is even. Hence, n = 2m, where m is a positive integer. Then,
(n + 2)(n + 4) =
(2m + 2)(2m + 4) =
2(m + 1)2(m + 2) =
4(m + 1)(m + 2) =
4 × (product of two consecutive positive integers, one which must be even) =
4 × (an even number), and this equals a number that is at least a multiple of 8
Hence, the answer is (D).
 Consecutive integers are written as x, x + 1, x + 2,…
Consecutive integers are written as x, x + 1, x + 2,…
 Consecutive even or odd integers are written as x, x + 2, x + 4,…
Consecutive even or odd integers are written as x, x + 2, x + 4,…
 The integer zero is neither positive nor negative, but it is even: 0 = 2 × 0.
The integer zero is neither positive nor negative, but it is even: 0 = 2 × 0.
 A prime number is an integer that is divisible only by itself and 1.
A prime number is an integer that is divisible only by itself and 1.
The prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41,…
 A number is divisible by 3 if the sum of its digits is divisible by 3.
A number is divisible by 3 if the sum of its digits is divisible by 3.
For example, 135 is divisible by 3 because the sum of its digits (1 + 3 + 5 = 9) is divisible by 3.
 A common multiple is a multiple of two or more integers.
A common multiple is a multiple of two or more integers.
For example, some common multiples of 2 and 5 are 0, 10, 20, 40, and 50.
 The least common multiple (LCM) of two integers is the smallest positive integer that is a multiple of both.
The least common multiple (LCM) of two integers is the smallest positive integer that is a multiple of both.
For example, the LCM of 4 and 10 is 20. The standard method of calculating the LCM is to prime factor the numbers and then form a product by selecting each factor the greatest number of times it occurs. For 4 and 10, we get
4 = 22
10 = 2 • 5
In this case, select 22 instead of 2 because it has the greater number of factors of 2, and select 5 by default since there are no other factors of 5. Hence, the LCM is 22 • 5 = 4 • 5 = 20.
For another example, let’s find the LCM of 8, 36, and 54. Prime factoring yields
8 = 23
36 = 22 • 32
54 = 2 • 33
In this case, select 23 because it has more factors of 2 than 22 or 2 itself, and select 33 because is has more factors of 3 than 32 does. Hence, the LCM is 23 • 33 = 8 • 27 = 216.
A shortcut for finding the LCM is to just keep adding the largest number to itself until the other numbers divide into it evenly. For 4 and 10, we would add 10 to itself: 10 + 10 = 20. Since 4 divides evenly in to 20, the LCM is 20. For 8, 36, and 54, we would add 54 to itself: 54 + 54 + 54 + 54 = 216. Since both 8 and 36 divide evenly into 216, the LCM is 216.
 The absolute value of a number, ||, is always positive. In other words, the absolute value symbol eliminates negative signs.
The absolute value of a number, ||, is always positive. In other words, the absolute value symbol eliminates negative signs.
For example, |–7| = 7 and |–π| = π. Caution, the absolute value symbol acts only on what is inside the symbol, | |. For example, –|–(7 – π)| = –(7 – π). Here, only the negative sign inside the absolute value symbol but outside the parentheses is eliminated.
[Numeric Entry question]
Example 3: The number of prime numbers divisible by 2 plus the number of prime numbers divisible by 3 is
A prime number is divisible by no other numbers, but itself and 1. Hence, the only prime number divisible by 2 is 2 itself; and the only prime number divisible by 3 is 3 itself. Hence, The number of prime numbers divisible by 2 is one, and the number of prime numbers divisible by 3 is one. The sum of the two is 1 + 1 = 2. Enter 2 in the grid.
Example 4: If 15x + 16 = 0, then 15|x| equals which one of the following?
(A) 15
(B) –16x
(C) 15x
(D) 16
(E) 16x
Solving the given equation 15x + 16 = 0 yields x = –16/15.
Substituting this into the expression 15|x| yields
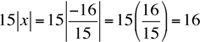
The answer is (D).
[Multiple-choice question – Select One or More Answer Choices]
Example 5: If |l5x + 2| = 4, then 15|x| =
(A) –6
(B) –2
(C) 0
(D) 2
(E) 6
|15x+ 2| = 4 yields two cases:
Case I: |
Case II: |
15x + 2 = –4 |
15x + 2 = 4 |
15x = –4 –2 = –6. |
15x = 4 – 2 = 2. |
Now, 15|x| = |15x| = |–6| = 6 = Choice (E). |
Now, 15|x| = |15x| = |2| = 2 = Choice (D). |
The answers are (D), and (E).
 The product (quotient) of positive numbers is positive.
The product (quotient) of positive numbers is positive.
 The product (quotient) of a positive number and a negative number is negative.
The product (quotient) of a positive number and a negative number is negative.
For example, –5(3) = –15 and 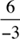 = –2.
= –2.
 The product (quotient) of an even number of negative numbers is positive.
The product (quotient) of an even number of negative numbers is positive.
For example, (–5)(–3)(–2)(–1) = 30 is positive because there is an even number, 4, of positives. 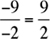 is positive because there is an even number, 2, of positives.
is positive because there is an even number, 2, of positives.
 The product (quotient) of an odd number of negative numbers is negative.
The product (quotient) of an odd number of negative numbers is negative.
For example, (–2)(–π)(–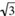 ) = –2π
) = –2π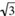 is negative because there is an odd number, 3, of negatives.
is negative because there is an odd number, 3, of negatives. 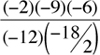 = –1 is negative because there is an odd number, 5, of negatives.
= –1 is negative because there is an odd number, 5, of negatives.
 The sum of negative numbers is negative.
The sum of negative numbers is negative.
For example, –3 – 5 = –8. Some students have trouble recognizing this structure as a sum because there is no plus symbol, +. But recall that subtraction is defined as negative addition. So –3 – 5 = –3 + (–5).
 A number raised to an even exponent is greater than or equal to zero.
A number raised to an even exponent is greater than or equal to zero.
For example, (–π)4 = π4 ≥ 0, and x2 ≥ 0, and 02 = 0 · 0 = 0 ≥ 0.
Problem Set E;
 Easy
Easy
[Multiple-choice question – Select One or More Answer Choices]
1. If x is divisible by both 3 and 4, then the number x must be a multiple of which of the following?
(A) 8
(B) 12
(C) 15
(D) 18
(E) 21
[Multiple-choice question – Select One or More Answer Choices]
2. The last digit of the positive even number n equals the last digit of n2. Which of the following could be n ?
(A) 10
(B) 14
(C) 15
(D) 16
(E) 17
[Multiple-choice Question – Select One or More Answer Choices]
3. Which of the following are divisible by both 2 and 3?
(A) 1005
(B) 1296
(C) 1351
(D) 1406
(E) 1414
(F) 3456
4. |
Column A |
Column B |
|
The number of prime numbers divisible by 2 |
The number of prime numbers divisible by 3. |
[Multiple-choice Question – Select One or More Answer Choices]
5. Which one of the following equals the product of exactly two prime numbers?
(A) 11 · 6
(B) 13 · 22
(C) 14 · 23
(D) 17 · 21
(E) 13 · 23
6. Which one of the following equals the product of the smallest prime number greater than 21 and the largest prime number less than 16?
(A) 13 · 16
(B) 13 · 29
(C) 13 · 23
(D) 15 · 23
(E) 16 · 21
7. |
Column A |
a and b are the digits of a two-digit number ab, and a = b + 3. |
Column B |
|
|
|
The two-digit number ab |
|
40 |
8. |
Column A |
|
Column B |
|
The last digit in the number 25256 |
|
The last digit in the number 15256 |
 Medium
Medium
9. |
Column A |
p and q are two positive integers and p/q = 7.15 |
Column B |
|
q |
|
15 |
10. |
Column A |
X is a 3-digit number and Y is a 4-digit number. All the digits of X are greater than 4, and all the digits of Y are less than 5. |
Column B |
|
The sum of the digits of X |
|
The sum of the digits of Y |
11. |
Column A |
|
Column B |
|
The least number divisible by 2, 3, 4, 5, and 6 |
|
The least number that is a multiple of 2, 3, 4, 5 and 6 |
[Numeric Entry Question]
12. The number 3 divides a with a result of b and a remainder of 2. The number 3 divides b with a result of 2 and a remainder of 1. What is the value of a ?
13. The remainder when the positive integer m is divided by 7 is x. The remainder when m is divided by 14 is x + 7. Which one of the following could m equal?
(A) 45
(B) 53
(C) 72
(D) 85
(E) 100
14. Which one of the following choices does not equal any of the other choices?
(A) 5.43 + 4.63–3.24–2.32
(B) 5.53 + 4.73–3.34–2.42
(C) 5.53 + 4.53–3.34–2.22
(D) 5.43 + 4.73–3.24–2.42
(E) 5.43 +4.73 –3.14 –2.22
[Numeric Entry Question]
15. Each of the two positive integers a and b ends with the digit 2. With which one of the following numbers does a – b end?
16. |
Column A |
x is a two-digit number. The digits of the number differ by 6, and the squares of the digits differ by 60. |
Column B |
|
x |
|
60 |
17. If each of the three nonzero numbers a, b, and c is divisible by 3, then abc must be divisible by which one of the following the numbers?
(A) 8
(B) 27
(C) 81
(D) 121
(E) 159
18. How many positive five-digit numbers can be formed with the digits 0, 3, and 5?
(A) 14
(B) 15
(C) 108
(D) 162
(E) 243
19. If n is a positive integer, which one of the following numbers must have a remainder of 3 when divided by any of the numbers 4, 5, and 6?
(A) 12n + 3
(B) 24n + 3
(C) 80n + 3
(D) 90n + 2
(E) 120n + 3
20. |
Column A |
|
Column B |
|
Least common multiple of the two positive integers m and n |
|
mn |
[Numeric Entry Question]
21. The number 3072 is divisible by both 6 and 8. Which one of the following is the first integer larger than 3072 that is also divisible by both 6 and 8?
[Numeric Entry Question]
22. If the least common multiple of m and n is 24, then what is the first integer larger than 3070 that is divisible by both m and n ?
23. |
Column A |
|
Column B |
|
The first number larger than 300 that is a multiple of both 6 and 8 |
|
324 |
24. |
Column A |
a, b, and c are consecutive integers in increasing order of size. |
Column B |
|
a/5 – b/6 |
|
b/5 – c/6 |
25. How many 3-digit numbers do not have an even digit or a zero?
(A) 20
(B) 30
(C) 60
(D) 80
(E) 125
26. |
Column A |
The digits of a two-digit number x differ by 4. |
Column B |
|
The positive difference between the squares of the digits of x |
|
15 |
 Hard
Hard
27. Which one of the following is the minimum value of the sum of two integers whose product is 36?
(A) 37
(B) 20
(C) 15
(D) 13
(E) 12
28. If a and b are positive integers, and x = 2 · 3 · 7 · a, and y = 2 · 2 · 8 · b, and the values of both x and y lie between 120 and 130 (not including the two), then a – b =
(A) –2
(B) –1
(C) 0
(D) l
(E) 2
29. |
Column A |
a and b are the digits of a two-digit number ab, and b = a + 3. |
Column B |
|
The positive two-digit number ab |
|
The positive two-digit number ba |
30. a, b, c, d, and e are five consecutive numbers in increasing order of size. Deleting one of the five numbers from the set decreased the sum of the remaining numbers in the set by 20%. Which one of the following numbers was deleted?
(A) a
(B) b
(C) c
(D) d
(E) e
31. A set has exactly five consecutive positive integers starting with 1. What is the percentage decrease in the average of the numbers when the greatest one of the numbers is removed from the set?
(A) 5
(B) 8.5
(C) 12.5
(D) 15.2
(E) 16.66
32. What is the maximum value of m such that 7m divides into 14! evenly? (n! means 1 · 2 · 3 · … · n)
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
33. |
Column A |
The sum of the positive integers from 1 through n can be calculated by the formula |
Column B |
|
|
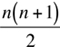
|
|
|
The sum of the multiples of 6 between 0 and 100 |
|
The sum of the multiples of 8 between 0 and 100 |
34. |
Column A |
A palindrome number is a number that reads the same forward or backward. For example, 787 is a palindrome number. |
Column B |
|
Smallest palindrome number greater than 233 |
|
Smallest palindrome greater than 239 |
 Very Hard
Very Hard
35. 2ab5 is a four-digit number divisible by 25. If the number formed from the two digits ab is a multiple of 13, then ab =
(A) 10
(B) 25
(C) 52
(D) 65
(E) 75
36. The positive integers m and n leave remainders of 2 and 3, respectively, when divided by 6. m > n. What is the remainder when m – n is divided by 6?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
[Numeric Entry Question]
37. The remainder when m + n is divided by 12 is 8, and the remainder when m – n is divided by 12 is 6. If m > n, then what is the remainder when mn divided by 6?
38. What is the remainder when 72 · 82 is divided by 6?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
39. |
Column A |
The positive integers m and n leave a remainder of 2 and 3, respectively, when divided by 6. m > n |
Column B |
|
The remainder when m + n is divided by 6 |
|
The remainder when m – n is divided by 6 |
Answers and Solutions to Problem Set E
 Easy
Easy
1. We are given that x is divisible by 3 and 4. Hence, x must be a common multiple of 3 and 4. The least common multiple of 3 and 4 is 12. So, x is a multiple of 12. The answer is (B).
2. Numbers ending with 0, 1, 5, or 6 will have their squares also ending with the same digit.
For example,
10 ends with 0, and 102 (= 100) also ends with 0.
11 ends with 1, and 112 (= 121) also ends with 1.
15 ends with 5, and 152 (= 225) also ends with 5.
16 ends with 6, and 162 (= 256) also ends with 6.
Among the four numbers 0, 1, 5, or 6, even numbers only end with 0 or 6. Choices (A) and (D) have such numbers. The answer is (A) and (D).
3. A number divisible by 2 ends with one of the digits 0, 2, 4, 6, or 8.
If a number is divisible by 3, then the sum of its digits is also divisible by 3.
Hence, a number divisible by both 2 and 3 will follow both of the above rules.
Choices (A) and (C) do not end with an even digit. Hence, eliminate them.
The sum of digits of Choice (B) is 1 + 2 + 9 + 6 = 18, which is divisible by 3. Also, the last digit is 6. Hence, choice (B) is correct.
This is also true with choice (F). The sum of digits of Choice (F) is 3 + 4 + 5 + 6 = 18, which is divisible by 3. Also, the last digit is 6. Hence, choice (F) is correct.
Next, the sum of the digits of choices (D) and (E) are 1 + 4 + 0 + 6 (= 11) and 1 + 4 + 1 + 4 (= 10), respectively, and neither is divisible by 3. Hence, reject the two choices.
Hence, the answer is (B) and (F).
4. A prime number is divisible by no other numbers, but itself and 1. Hence, the only prime number divisible by 2 is 2 itself; and the only prime number divisible by 3 is 3 itself. Since the number of primes in each column is 1, the answer is (C).
5. Choice (A): 11 · 6 can be factored as 11 · 2 · 3. The product of more than two primes. Reject.
Choice (B): 13 · 22 can be factored as 13 · 2 · 11. The product of more than two primes. Reject.
Choice (C): 14 · 23 can be factored as 7 · 2 · 23. The product of more than two primes. Reject.
Choice (D): 17 · 21 can be factored as 17 · 3 · 7. The product of more than two primes. Reject.
Choice (E): 13 · 23 cannot be further factored and is itself the product of two primes. Accept.
The answer is (E).
6. The smallest prime number greater than 21 is 23, and the largest prime number less than 16 is 13. The product of the two is 13 · 23, which is listed in choice (C). The answer is (C).
7. Suppose b equals 0. Then a = b + 3 = 0 + 3 = 3. Hence, Column A equals ab = 30. Here, Column A is less than Column B, which equals 40.
Now, suppose b equals 1. Then a = b + 3 = 1 + 3 = 4. Hence, Column A equals ab = 41. Here Column A is greater than Column B, which equals 40.
Hence, we have a double case, and the answer is (D).
8. The last digit of the number 252 (in Column A) is 2, and the last digit of the number 152 (in Column B) is also 2. Hence, both numbers raised to the same power (here 56) should end with the same digit. So, 15256should end with the same digit as 25256. The answer is (C). A small example: the last digit of 62 (= 36) is 6and the last digit of 162 (= 256) is also 6.
 Medium
Medium
9. We have that p/q = 7.15. Solving for p yields p = 7.15q – 7q + 0.15q = 7(a positive integer) + 0.15q = (a positive integer) + 0.15q. Now, p is a positive integer only when 0.15q is an integer. Now, 0.15q equals 15/100 · q = 3q/20 and would result in an integer only when the denominator of the fraction (i.e., 20) is canceled out by q. This happens only when q is a multiple of 20. Hence, q = 20, or 40, or 60,.… Any of these values is greater than 15. Hence, Column A is greater than Column B, and the answer is (A).
10. Column A: Since all the digits of the 3-digit number X are greater than 4, each digit must be greater than or equal to 5. Hence, the sum of the three digits must be greater than or equal to 3 × 5 = 15. Also, since the maximum value of each digit is 9, the maximum possible value of the sum of its digits is 3 × 9 = 27. Hence, we have the inequality 15 ≤ Column A ≤ 27.
Column B: Since all the digits in the 4-digit number Y are less than 5, each digit must be less than or equal to 4. Hence, the sum of the four digits must be less than or equal to 4 × 4 = 16. Also, the minimum value of the sum of the digits of a 4-digit number is 1 (for example, for 1000, the sum of the digits is 1). Hence, we have the inequality 1 ≤ Column B ≤ 16.
Since the inequality for Column A, 15 ≤ Column A ≤ 27, and the inequality for Column B, 1 ≤ Column B ≤ 16, have a common range (numbers between 15 and 16, inclusive, satisfy both inequalities), an inequality between the two columns cannot be derived. Hence, we cannot know which column is greater. The answer is (D).
11. Any number that is divisible by the five numbers 2, 3, 4, 5, and 6 must also be a multiple of all five numbers. So, Column A (refers to the set of numbers that are divisible by 2, 3, 4, 5, and 6) and Column B (refers to the set of numbers that are a multiple of 2, 3, 4, 5 and 6) refer to the same set. Hence, the least values of the two columns are the same. So, Column A equals Column B, and the answer is (C).
12. Since 3 divides b with a result of 2 and a remainder of 1, b = 2 · 3 + 1 = 7. Since number 3 divides a with a result of b (which we now know equals 7) and a remainder of 2, a = b · 3 + 2 = 7 · 3 + 2 = 23. Hence, enter 23 in the grid.
13. Choice (A): 45/7 = 6 + 3/7, so x = 3. Now, 45/14 = 3 + 3/14. The remainder is 3, not x + 7 (= 10). Reject.
Choice (B): 53/7 = 7 + 4/7, so x = 4. Now, 53/14 = 3 + 11/14. The remainder is 11, and equals x + 7 (= 11). Accept the choice.
Choice (C): 72/7 = 10 + 2/7, so x = 2. Now, 72/14 = 5 + 2/14. The remainder is 2, not x + 7 (= 9). Reject.
Choice (D): 85/7= 12+ 1/7, so x = 1. Now, 85/14 = 6 + 1/14. The remainder is 1, not x + 7 (= 8). Reject.
Choice (E): 100/7 = 14 + 2/7, so x = 2. Now, 100/14 = 7 + 2/14. The remainder is 2, not x + 7 (= 9). Reject.
The answer is (B).
14. Choice (A) = 5.43 + 4.63 – 3.24 – 2.32 = 4.5.
Choice (B) = 5.53 + 4.73 – 3.34 – 2.42 = 4.5 = Choice (A). Reject choices (A) and (B).
Choice (C) = 5.53 + 4.53 – 3.34 – 2.22 = 4.5 = Choice (A). Reject choice (C).
Choice (D) = 5.43 + 4.73 – 3.24 – 2.42 = 4.5 = Choice (A). Reject choice (D).
Choice (E) = 5.43 + 4.73 – 3.14 – 2.22 = 4.8. Correct.
The answer is (E).
15. Since each of the two integers a and b ends with the same digit, the difference of the two numbers ends with 0. For example 642 – 182 = 460, and 460 ends with 0. Enter 0 in the grid.
16. Suppose a and b are the two digits of the number x, and let a represent the greater of the two. From the given information, we have
a – b = 6 |
(1) |
a2 – b2 = 60 |
|
Applying the Difference of Squares formula, a2 – b2 – (a – b)(a + b), to the second equation yields
(a – b)(a + b) = 60 |
|
6(a + b) = 60 |
since a – b = 6 |
a + b = 60/6 = 10 |
(2) |
Adding equations (1) and (2) yields 2a = 16. Dividing by 2 yields a = 8. Substituting this in equation (2) yields 8 + b = 10. Solving for b yields b = 2. Hence, the two digits are 2 and 8. They can be arranged in any order. Hence, 28 and 82 are two feasible solutions. Now, 28 is less than Column B, and 82 is greater than Column B. Hence, we have a double case, and the answer is (D).
17. Since each one of the three numbers a, b, and c is divisible by 3, the numbers can be represented as 3p, 3q, and 3r, respectively, where p, q, and r are integers. The product of the three numbers is 3p · 3q · 3r = 27(pqr). Since p, q, and r are integers, pqr is an integer and therefore abc is divisible by 27. The answer is (B).
18. Let the digits of the five-digit positive number be represented by 5 compartments:

Each of the last four compartments can be filled in 3 ways (with any one of the numbers 0, 3 and 5).
The first compartment can be filled in only 2 ways (with only 3 and 5, not with 0, because placing 0 in the first compartment would yield a number with fewer than 5 digits).
Hence, the total number of ways the five compartments can be filled in is 2 · 3 · 3 · 3 · 3 = 162. The answer is (D).
19. Let m be a number that has a remainder of 3 when divided by any of the numbers 4, 5, and 6. Then m – 3 must be exactly divisible by all three numbers. Hence, m – 3must be a multiple of the Least Common Multiple of the numbers 4, 5, and 6. The LCM is 3 · 4 · 5 = 60. Hence, we can suppose m – 3= 60n, where p is a positive integer. Replacing p with n, we get m – 3= 60n. So, m = 60n + 3. Choice (E) is in the same format 120n + 3 = 60(2n) + 3. Hence, the answer is (E).
We can also subtract 3 from each answer-choice, and the correct answer will be divisible by 60:
Choice (A): If n = 1, then (12n + 3) – 3 = 12n = 12, not divisible by 60. Reject.
Choice (B): If n = 1, then (24n + 3) – 3 = 24n = 24, not divisible by 60. Reject.
Choice (C): If n = 1, then (80n + 3) – 3 = 80n = 80, not divisible by 60. Reject.
Choice (D): If n = 1, then (90n + 2) – 3 = 90n – 1 = 89, not divisible by 60. Reject.
Choice (E): (120n + 3) – 3 = 120n, divisible by 60 for any integer n. Hence, correct.
20. Suppose the two positive integers m and n do not have a common factor, apart from 1. Then the LCM of m and n is mn. For example, when m = 14 (= 2 · 7) and n = 15 (= 3 · 5), the LCM is 14 · 15. In this case, the LCM equals mn, and the Column A equals Column B.
Now, suppose the two integers m and n have at least one common factor (other than 1). Then the LCM uses the common factors only once, unlike mn. Hence, the LCM is less than mn. For example, suppose m = 10 (= 2 · 5) and n = 14 (= 2 · 7). Here, m and n have 2 as a common factor. The LCM of m and nis2·5·7 = 70, and mn equals 2·5·2·7= 140. The LCM did not use the underlined 2 in the evaluation. Hence, here, Column A is less than Column B.
Since this is a double case, the answer is (D).
21. Any number divisible by both 6 and 8 must be a multiple of the least common multiple of the two numbers, which is 24. Hence, any such number can be represented as 24n. If 3072 is one such number and is represented as 24n, then the next such number should be 24(n + 1) = 24n + 24 = 3072 + 24 = 3096. Hence, enter 3096 in the grid.
22. Any number divisible by both m and n must be a multiple of the least common multiple of the two numbers, which is given to be 24. The first multiple of 24 greater than 3070 is 3072. Hence, enter 3072 in the grid.
23. The least common multiple of 6 and 8 is 24. Hence, a multiple of both 6 and 8 must also be a multiple of 24.
We know that a multiple of 24 exists once in every 24 consecutive numbers. For example, between the numbers 34 (not itself a multiple of 24) and 34 + 24, there must be exactly one multiple of 24. Similarly, exactly one multiple of 24 must exist between 300 (not itself a multiple of 24) and 300 + 24 (= 324, Column B), and this number is the first multiple of 24 larger than 300, Column A. So, Column A lies between 300 and 324 (Column B) and therefore is less than Column B. The answer is (B).
24. The consecutive integers a, b, and c in the increasing order of size can be expressed as a, a + 1, a + 2, respectively.
Now, Column A equals 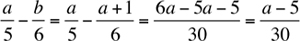
Column B equals

Since Column B is 1/30 units greater than Column A, the answer is (B).
25. There are 5 digits that are not even or zero: 1, 3, 5, 7, and 9. Now, let’s count all the three-digit numbers that can be formed from these five digits. The first digit of the number can be filled in 5 ways with any one of the mentioned digits. Similarly, the second and third digits of the number can be filled in 5ways. Hence, the total number of ways of forming the three-digit number is 125 (= 5 × 5 × 5). The answer is (E).
26. Since the digits of the number differ by 4, the number can be any one of the numbers 15, 26, 37, 48, and 59 or any one of their reverse numbers. Hence, the positive difference between the digits varies from 52 – I2 = 24 (for the numbers 15 or 51) to 92 – 52 = 56 (for the numbers 59 or 95). Hence, Column A is a number between 24 and 56, inclusive, and therefore is always greater than 15, the value of Column B. Hence, the answer is (A).
 Hard
Hard
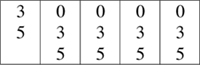
27. List all possible factors x and y whose product is 36, and calculate the corresponding sum x + y:
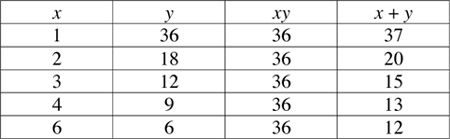
From the table, the minimum sum is 12. The answer is (E).
28. We are given that x = 2 · 3 · 7 · a = 42a and y = 2 · 2 · 8 · b = 32b.
We are given that the values of both x and y lie between 120 and 130 (not including the two).
The only multiple of 42 in this range is 42 × 3 = 126. Hence, x = 126 and a = 3. The only multiple of 32 in this range is 32 × 4 = 128. Hence, y = 128 and b = 4. Hence, a – b = 3 – 4 = –1. The answer is (B).
29. Since b – a + 3, the digit b is greater than the digit a and a – b = 3.
In a two-digit number, the leftmost digit (the tens-digit) is the “more significant” digit. Since b > a, the number ba (which has b in tens-digit position) is greater than the number ab (which has a in tens-digit position). Hence, Column B is greater than Column A, and the answer is (B).
Method II
Column A: ab = 10a + b.
Column B: ba = 10b + a.
Column A – Column B = 10a + b = (10b + a) = 9a – 9b = 9(a – b) = 9(–3) = –27.
Hence, Column A is 27 units less than Column B. The answer is (B).
30. Since a, b, c, d, and e are consecutive numbers in the increasing order, we have b = a + l, c = a + 2, d = a + 3 and e = a + 4. The sum of the five numbers is a + (a + 1) + (a + 2) + (a + 3) + (a + 4) = 5a + 10.
Now, we are given that the sum decreased by 20% when one number was deleted. Hence, the new sum should be (5a + 10)(1 – 20/100) = (5a + 10)(1 – 1/5) = (5a + 10)(4/5) = 4a + 8. Now, since New Sum = Old Sum – Dropped Number, we have (5a + 10) = (4a + 8) + Dropped Number. Hence, the number dropped is (5a + 10) – (4a + 8) = a + 2. Since c – a + 2, the answer is (C).
31. The average of the five consecutive positive integers 1, 2, 3, 4, and 5 is (1 + 2 + 3 + 4 + 5)/5 = 15/5 = 3. After dropping 5 (the greatest number), the new average becomes (1 + 2 + 3 + 4)/4 = 10/4 = 2.5. The percentage drop in the average is
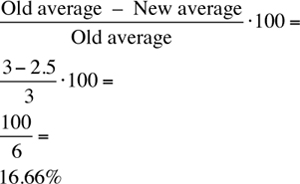
The answer is (E).
32. The term 14! equals the product of the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, and 14. Only two of these numbers are divisible by 7. The numbers are 7 and 14. Hence, 14! can be expressed as the product of k · 7 · 14, where k is not divisible by 7. Now, since there are two 7s in 14!, the numbers 7 and 72 divide 14! evenly. 73 and further powers of 7 leave a remainder when divided into 14!. Hence, the maximum value of m is 2. The answer is (B).
33. The sum of the multiples of 6 between 0 and 100 equals
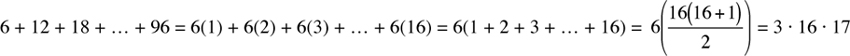
The sum of multiples of 8 between 0 and 100 equals
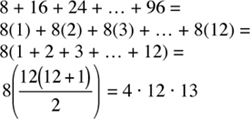
Since 3 · 16 · 17 (= 48 · 17) is clearly greater than 4 · 12 · 13 (= 48 · 13), Column A is greater than Column B and the answer is (A).
34. A palindrome number reads the same forward or backward. There is no palindrome number between 233 through 239 since none of the numbers read the same both forward and backward. Hence, the palindrome number immediately after 233 is the same as the palindrome number immediate after 239. Hence, Column A and Column B refer to the same number, and the answer is (C).
 Very Hard
Very Hard
35. We have that the number 2ab5 is divisible by 25. Any number divisible by 25 ends with the last two digits 00, 25, 50, or 75. So, b5 should equal 25 or 75. Hence, b = 2 or 7. Since a is now free to take any digit from 0 through 9, ab can have multiple values.
We also have that ab is divisible by 13. The multiples of 13 are 13, 26, 39, 52, 65, 78, and 91. Among these, the only number ending with 2 or 7 is 52. Hence, ab – 52. The answer is (C).
36. We are given that the numbers m and n, when divided by 6, leave remainders of 2 and 3, respectively. Hence, we can represent the numbers m and n as 6p + 2 and 6q + 3, respectively, where p and q are suitable integers.
Now, m – n – (6p + 2) – (6q + 3) = 6 – 6q – 1 = 6(p – q) – 1. A remainder must be positive, so let’s add 6 to this expression and compensate by subtracting 6:
6(p – 9) – 1 =
6(p – q) – 6 + 6 – 1 =
6(p – q) – 6 + 5 =
6(p – q – 1) + 5
Thus, the remainder is 5, and the answer is (E).
37. Since the remainder when m + n is divided by 12 is 8, m + n = 12p + 8; and since the remainder when m – n is divided by 12 is 6, m – n – 12q + 6. Here, p and q are integers. Adding the two equations yields 2m – 12p + 12q + 14. Solving for m yields m – 6p + 6q + 7 – 6(p + q + 1) + 1 = 6r + 1, where r is a positive integer equaling p + q + 1. Now, let’s subtract the equations m + n – 12p + 8 and m – n = 12q + 6. This yields 2n – (12p + 8) – (12q + 6) = 12(p – q) + 2. Solving for n yields n – 6(p – q) + 1 = 6t + 1, where t is an integer equaling p – q.
Hence, we have
mn = (6r + 1)(6t + 1)
= 36rt + 6r + 6t + 1
= 6(6rt + r + t) + 1 by factoring out 6
Hence, the remainder is 1. Enter 1 in the grid.
38. 72 · 82 = (7 · 8)2 = 562.
The number immediately before 56 that is divisible by 6 is 54. Now, writing 562 as (54 + 2)2, we have

Since the remainder is 4, the answer is (D).
39. We are given that the numbers m and n, when divided by 6, leave remainders of 2 and 3, respectively. Hence, we can represent the numbers m and n as 6p + 2 and 6q + 3, respectively, where p and q are suitable integers.
Now, m + n – (6p + 2) + (6q + 3) – 6p + 6q + 5 – 6(p + q) + 5; the remainder is 5. Hence, Column A equals 5.
Now, m – n = (6p + 2) – (6q + 3) = 6p – 6q – 1 = 6(p – q) – 1. A remainder must be positive, so let’s add 6 to this expression and compensate by subtracting 6:
6(p – q) – 1 =
6(p – q) – 6 + 6 – 1 =
6(p – q) – 6 + 5 =
6(p – q – 1) + 5
Thus, the remainder is 5, and Column B equals 5.
Since both columns equal 5, the answer is (C).
 “The remainder is r when p is divided by k” means p = kq + r, the integer q is called the quotient. For instance, “The remainder is 1 when 7 is divided by 3” means 7 = 3 · 2 + 1. Dividing both sides of p = kq + r by k gives the following alternative form p/k = q + r/k.
“The remainder is r when p is divided by k” means p = kq + r, the integer q is called the quotient. For instance, “The remainder is 1 when 7 is divided by 3” means 7 = 3 · 2 + 1. Dividing both sides of p = kq + r by k gives the following alternative form p/k = q + r/k.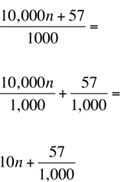

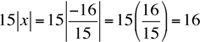
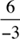 = –2.
= –2.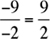 is positive because there is an even number, 2, of positives.
is positive because there is an even number, 2, of positives.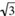 ) = –2π
) = –2π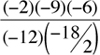 = –1 is negative because there is an odd number, 5, of negatives.
= –1 is negative because there is an odd number, 5, of negatives.