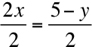
When simplifying algebraic expressions, we perform operations within parentheses first and then exponents and then multiplication and then division and then addition and lastly subtraction. This can be remembered by the mnemonic:
PEMDAS
Please Excuse My Dear Aunt Sally
When solving equations, however, we apply the mnemonic in reverse order: SADMEP. This is often expressed as follows: inverse operations in inverse order. The goal in solving an equation is to isolate the variable on one side of the equal sign (usually the left side). This is done by identifying the main operation–addition, multiplication, etc.–and then performing the opposite operation.
Example: Solve the following equation for je: 2x + y = 5
Solution: The main operation is addition (remember addition now comes before multiplication, SADMEP), so subtracting y from both sides yields
2x + y – y = 5 – y
Simplifying yields 2x = 5 – y
The only operation remaining on the left side is multiplication. Undoing the multiplication by dividing both sides by 2 yields
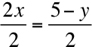
Canceling the 2 on the left side yields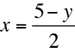 
Example: Solve the following equation for x: 3x - 4 = 2(x – 5)
Solution: Here x appears on both sides of the equal sign, so let’s move the x on the right side to the left side. But the x is trapped inside the parentheses. To release it, distribute the 2:
3x – 4 = 2x – 10
Now, subtracting 2x from both sides yields*
x –4 = –10
Finally, adding 4 to both sides yields
x = –6
We often manipulate equations without thinking about what the equations actually say. The GRE likes to test this oversight. Equations are packed with information. Take for example the simple equation 3x + 2 –5. Since 5 is positive, the expression 3x + 2 must be positive as well. An equation means that the terms on either side of the equal sign are equal in every way. Hence, any property one side of an equation has the other side will have as well. Following are some immediate deductions that can be made from simple equations.
* Note, students often mistakenly add 2x to both sides of this equation because of the minus symbol between 2x and 10. But 2x is positive, so we subtract it. This can be seen more clearly by rewriting the right side of the equation as –10 + 2x.
Equation |
Deduction |
y – x = 1 |
y > x |
y2 = x2 |
y = ± x, or |y| = |x|. That is, x and y can differ only in sign. |
y3 = x3 |
y = x |
y = x2 |
y ≥ 0 |
|
y > 0 |
|
Both x and y are positive or both x and y are negative. |
x2 + y2 = 0 |
y = x = 0 |
3y = 4x and x > 0 |
y > x and y is positive. |
3y = 4x and x < 0 |
y < x and y is negative. |
|
y ≥ 0 and x ≥ –2 |
y = 2x |
y is even |
y = 2x + 1 |
y is odd |
yx = 0 |
y = 0 or x = 0, or both |
In Algebra, you solve an equation for, say, y by isolating y on one side of the equality symbol. On the GRE, however, you are often asked to solve for an entire term, say, 3 – y by isolating it on one side.
Example: If a + 3a is 4 less than b + 3b, then a – b =
(A) –4
(B) –1
(C) 1/5
(D) 1/3
(E) 2
Translating the sentence into an equation gives |
a + 3a = b + 3b – 4 |
Combining like terms gives |
4a – 4b – 4 |
Subtracting 4b from both sides gives |
4a – 4b = –4 |
Finally, dividing by 4 gives |
a – b = –1 |
Hence, the answer is (B). |
|
Sometimes on the GRE, a system of 3 equations will be written as one long “triple” equation. For example, the three equations x = y, y = z, x = z, can be written more compactly as x = y = z.
Example: If w ≠ 0 and w = 2x = 
y, what is the value of w – x in terms of y ?
(A) 2y
(B) 
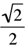y
(C)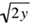 
(D) 
(E) y
The equation w = 2x = y stands for three equations: w = 2x, 2x = y, and w = y. From the last equation, we get w = y; and from the second equation, we get x = 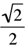y. Hence,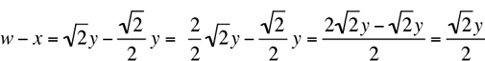 
Hence, the answer is (B).
Often on the GRE, you can solve a system of two equations in two unknowns by merely adding or subtracting the equations–instead of solving for one of the variables and then substituting it into the other equation.
If p and q are positive, p2 + q2 = 16, and p2 – q2 = 8, then q =
(A) 2
(B) 4
(C) 8
(D) 2
(E) 2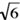
Subtract the second equation from the first: |
p2 + q2 = 16 |
|
(–) p2 – q2 = 8 |
|
2q2 = 8 |
Dividing both sides of the equation by 2 gives |
q2 =4 |
Finally, taking the square root of both sides gives |
q = ±2 |
Hence, the answer is (A). |
|
METHOD OF SUBSTITUTION (Four-Step Method)
Although on the GRE you can usually solve a system of two equations in two unknowns by merely adding or subtracting the equations, you still need to know a standard method for solving these types of systems.
The four-step method will be illustrated with the following system:
2x + y = 10
5x – 2y = 7
1) Solve one of the equations for one of the variables:
Solving the top equation for y yields y =10 – 2x.
2) Substitute the result from Step 1 into the other equation:
Substituting y = 10 – 2x into the bottom equation yields 5x = 2(10 – 2x) = 7.
3) Solve the resulting equation:
5x – 2(10 – 2x) = 7
5x – 20 + 4x = 7
9x – 20 = 7
9x = 27
x = 3
4) Substitute the result from Step 3 into the equation derived in Step 1 :
Substituting x = 3 into y = 10 – 2x yields y = 10 – 2(3) = 10 – 6 = 4.
Hence, the solution of the system of equations is the ordered pair (3,4).
Easy
1. If x = y and x + y = 10, then 2x + y =
(A) 3
(B) 15
(C) 18
(D) 24
(E) 30
2. |
Column A |
x + y = 1 |
Column B |
|
x |
|
y |
3. |
Column A |
7x + 3y = 12 |
Column B |
|
|
3x + 7y = 8 |
|
|
x – y |
|
1 |
4. If 4p is equal to 6q, then 2p – 3q equals which one of the following?
(A) 0
(B) 2
(C) 3
(D) 4
(E) 6
5. Which one of the following must equal p + q, if x – y = p and 2x + 3y = q ?
(A) x + y
(B) 3x –2y
(C) 2x –3?
(D) 2x + 3y
(E) 3x + 2y
6. If l + t = 4 and l + 3t = 9, then which one of the following equals l + 2t ?
(A) 13/2
(B) 19/2
(C) 15/2
(D) 17/3
(E) 21/4
7. If (x – y)(x + y) = 15 and x + y = x5, then what is the value of x/y ?
(A) 3
(B) 4
(C) 5
(D) 10
(E) 15
8. If x – 4y = 1 and y = x/2 + 1, then what is the value of x ?
(A) –5
(B) –2
(C) 2
(D) 5
(E) 8
9. If x2 – 4x + 3 equals 0, then what is the value of (x = 2)2?
(A) 0
(B) l
(C) 2
(D) 3
(E) 4
[Multiple-choice Question – Select One or More Answer Choices]
10. If x = a + 2 and b = x + 1, then which of the following must be false?
(A) a > b
(B) a < b
(C) a = b
(D) a = b2
(E) b = a2
11. If p is the sum of q and r, then which one of the following must equal q – r ?
(A) p – r
(B) p + r
(C) p – 2r
(D) p + 2r
(E) 2q – p
12. The sum of two numbers is 13, and their product is 30. What is the sum of the squares of the two numbers?
(A) –229
(B) –109
(C) 139
(D) 109
(E) 229
13. If p + q = 7 and pq = 12, then what is the value of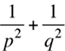 
?
(A) 1/6
(B) 25/144
(C) 49/144
(D) 7/12
(E) 73/144
14. If 2x + 3y = 11 and 3y + 2y = 9, then x + y =
(A) 4
(B) 7
(C) 8
(D) 9
(E) 11
[Multiple-choice Question – Select One or More Answer Choices]
15. If 2x – 2y + 1, then which of the following could be true?
(A) x > y
(B) x < y
(C) x = y
(D) x = y + 1
(E) 9x + 12y = 36
16. If 3x + y = x + 2y, then 2x – y =
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
17. If yz – zx = 3 and zx – xy = 4, then xy – yz =
(A) –7
(B) 1
(C) 3
(D) 4
(E) 7
18. If (x + 5) +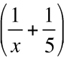 
= 5, then x =
(A) –5
(B) 1/2
(C) 1
(D) 5
(E) 10
19. If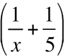 
= 4, then x =
(A) 1/5
(B) 1/2
(C) 1
(D) 5
(E) 10
20. |
Column A |
x + y = 7 |
Column B |
|
x + y2 |
|
3 + 42 |
21. If both expressions x2 – 3x + 2 and x2 – 4x + 3 equal 0, then what is the value of (x – 3)2?
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
22. If 42.42 = k(14 + 7/50), then what is the value of k ?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
23. If |2x – 4| is equal to 2 and (x – 3)2 is equal to 4, then what is the value of x ?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
24. If (a + 2)(a – 3)(a + 4) = 0 and a >0, then a =
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
Hard
25. If x + y = 7 and x2 + y2 = 25, then which one of the following equals the value of x3 + y3?
(A) 7
(B) 25
(C) 35
(D) 65
(E) 91
26. A system of equations is as shown below
x + l = 6
x – m = 5
x + p = 4
x – q = 3
What is the value of l + m + p + q ?
(A) 2
(B) 3
(C) 4
(D) 5
(E) 6
27. If mn = 3 and 1/m + 1/n = 4/3, then what is the value of 0.1 + 0.11/m + O.11/n?
(A) 0.2 + 0.11/3
(B) 0.1 + 0.11/3 + 0.11/2
(C) 0.1 + 0.14/3 + 0.11/2
(D) 0.1 + 0.11/3 + 0.13/2
(E) 0.1 + 0.11/4 + 0.11/2
28. a, b, and c are three different numbers, none of which equals the average of the other two. If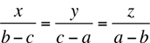 
, then x + y + z =
(A) 0
(B) 1/2
(C) 1/3
(D) 2/3
(E) 3/4
Very Hard
29. If a, b, and c are not equal to 0 or 1 and if ax = b, by = c, and cz = a, then xyz =
(A) 0
(B) 1
(C) 2
(D) a
(E) abc
Answers and Solutions to Problem Set O
Easy
1. Substituting x = y into the equation x + y = 10 yields x + x = 10. Combining like terms yields 2x = 10. Finally, dividing by 2 yields x = 5. Hence, 2x + y = 2(5) + 5 = 15. The answer is (B).
2. If x = y = 1/2, then x + y = 1/2 + 1/2 = 1 and the columns are equal.
But if x = 1 and y = 0, then x + y = 1 + 0 = 1 and Column A is larger than Column B.
Hence, we have a double case, and the answer is (D).
3. We are given the two equations:
7x + 3y = 12
3x + 7y = 8
Subtracting the bottom equation from the top equation yields
(7x + 3y) – (3x + 7y) = 12 – 8
7x + 3y – 3x – 7y = 4
4x – 4y = 4
4(x – y) = 4
x – y = 1
Hence, Column A equals 1; and since Column B also equals 1, the answer is (C).
4. We are given that 4p = 6q. Dividing both sides by 2 yields 2p = 3q. Subtracting 3q from both sides yields 2p – 3q = 0. The answer is (A).
5. We are given the equations x – y = p and 2x + 3y = q. Adding the two equations yields
(x – y) + (2x + 3y) = p + q
x – y + 2x + 3y = p + q
3x + 2y = p + q.
Hence, p + q = 3x + 2y. The answer is (E).
6. Adding the two given equations l + t = 4 and l + 3t = 9 yields
(l + t) + (l + 3t) = 4 + 9
2l + 4t = 13
l + 2t = 13/2 |
by dividing both sides by 2 |
The answer is (A).
7. We are given
(x – y)(x + y) x = 15 . . .(A)
x + y = 5 . . .(B)
Substituting the bottom equation in the top one yields (x – y)(5) = 15, or x – y = 15/5 = 3.
Adding this equation to equation (B) yields
x + y + (x – y) = 5 + 3
2x = 8
x = 8/2 = 4
Substituting this result in equation (B) yields 4 + y = 5, or y = 1.
Hence, x/y = 4/1 = 4.
The answer is (B).
8. We have the system of equations
x – 4y = 1
y = x/2 + 1
Substituting the bottom equation in to the top yields
x – 4(x/2 + 1) = 1
x – 2x – 4 = 1
–x = 4 + 1
x = –5
The answer is (A).
Medium
9. We have x2 – 4x + 3 = 0. By the Perfect Square Trinomial formula, (x – 2)2 = x2 – 4x + 4; and this equals (x2 – 4x + 3) + 1 = 0 + 1 = 1. Hence, the answer is (B).
10. We have the equations x = a + 2 and b = x + 1. Substituting the first equation into the second equation yields b = (a + 2)+ 1 = a + 3. This equation shows that b is 3 units greater than a. Hence, b must be greaterthan a. So, (B) is an answer–not (A) or (C), which contradict (B).
Next, assume a = b2 [Choice (D)]. Then a must be positive. If a is between 0 and 1, b is also between 0 and 1, which violates b = a + 3. Here, our assumption fails. If a were greater than 1, then b equals √a, which must be less than a – but we know that b is greater than a. Again, our assumption fails. Accept choice (D).
Next, assume b = a2 [Choice (E)]. This could be true. For example, consider b = a + 3 = a2. Subtracting a and 3 from both sides yields a2 – a – 3 = 0. The quadratic equation is in the form ax2 + bx + c = 0. Since the discriminant, b2 – 2ac = (–1)2 – 2(1)(–3) = 1 + 6 = 7, is positive, we will have valid solutions, which means that b = a2 is possible with given information. Hence, reject this choice (remember, we are looking for answers that must be false).
The answer is (B) and (D).
11. We are given that p = q + r. Now, let’s create the expression q – r by subtracting 2r from both sides of this equation:
p – 2r = q + r – 2r
or
p – 2r = q – r
The answer is (C).
12. Let the two numbers be x and y. Since their sum is 13, x + y = 13. Since their product is 30, xy = 30. Solving the equation xy = 30 for y yields y = 30/x. Plugging this into the equation x + y = 13 yields
x + 30/x = 13 |
|
x2 + 30 = 13x |
by multiplying both sides of the equation by x |
x2 – 13x + 30 = 0 |
by subtracting 13x from both sides of the equation |
(x – 3)(x – 10) = 0 |
|
x = 3 or x = 10 |
|
Now, if x = 3, then y = 13 – x = 13 – 3 = 10. Hence, x2 + y2 = 32 + 102 = 9 + 100 = 109. The answer is (D).
Method II:
(x + y)2 = x2 + y2 + 2xy. Hence, x2 + y2 = (x + y)2 – 2xy = 132 – 2(30) = 169 – 60 = 109.
13. Solving the equation p + q = 7 for q yields q = 7 – p. Plugging this into the equation pq = 12 yields
p(7–p) = 12
7p – p2 = 12
p2 – 7p + 12 = 0
(p – 3)(p – 4) = 0
p – 3 = 0 or p – 4 = 0
p = 3 or p = 4
If p = 3, then q = 7 – p = 7 – 3 = 4. Plugging these values into the expression 
yields
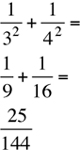
The result is the same for the other solution p = 4 (and then q = 7 – p = 7 – 4 = 3). The answer is (B).
Method II:
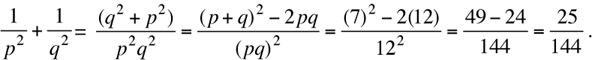The answer is (B).
14. Adding the two equations 2x + 3y = 11 and 3x + 2y = 9 yields 5x + 5y = 20, or x + y = 20/5 = 4. The answer is (A).
15. Dividing the equation 2x = 2y + 1 by 2 yields x = y + 1/2. Reading the equation yields “x is 1/2 unit greater than y.” Or more simply, x > y. So, (A) is an answer–automatically making (B) and (C) false.
Choice (D), x = y + 1, clearly violates the equation x = y + 1/2. Hence, choice (D) is not possible. Reject.
Choice (E): Solving the equation 9x + 12y = 36 for x yields x = –4y/3 + 4, which is an equation with slope different from the slope of given equation x = y + 1/2. Hence, the two lines intersect at some point, and at the point, choice (E) must be true.
The answer is (A) and (E).
16. Subtracting x and 2y from both sides of the given equation 3x + y = x + 2y yields
3x + y – x – 2y = x + 2y – x – 2y
2x – y = 0
The answer is (A).
17. Adding the two given equations yields
(yz – zx) + (zx – xy) = 3 + 4
yz – zx + zx – xy = 7
yz – xy = 7
xy – yz = –7 |
multiplying both sides by –1 |
The answer is (A).
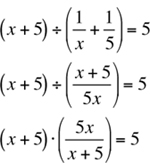
5x = 5
x = 1
The answer is (C). Note: If you solved the equation without getting a common denominator you may have gotten –5 as a possible solution. But, –5 is not a solution. Why?*
19. We are given the equation
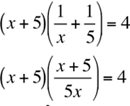
(x + 5)2 = 4x(5)
(x2 + 52 = 2x(5) = 4x(5) |
since (a + b)2 = a2 + b2 + 2ab |
x2 + 52 – 2x(5) = 0 |
|
(x – 5)2 = 0 |
since (a + b)2 = a2 + b2 – 2ab |
(x – 5) = 0 |
by taking the square root of both sides |
x = 5 |
|
The answer is (D).
20. We have the system of equations
x + y = 7
x2 + y2 = 25
Solving the top equation for y yields y = 7 – x. Substituting this into the bottom equation yields
x2 + (7 – x)2 = 25
x2 + 49 – 14x + x2 = 25
2x2 – 14x + 24 = 0
x2 – 7x + 12 = 0
(x2 – 3)(x – 4) = 0
x – 3 = 0 or x – 4 = 0
x = 3 or x = 4
Now, if x = 3, then y = 7 – 3 = 4 and Column A equals x + y2 = 3 + 42 (= Column B); and if x = 4, then y = 7 – 4 = 3 and Column A = x + y2 = 4 + 32 (≠ Column B). Hence, we have a double case, and the answer is (D).
* Because -5 is not in the domain of the original equation since it causes the denominator to be 0. When you solve an equation, you are only finding possible solutions. The “solutions” may not work when plugged back into the equation.
21. We have the equation x2 – 3x + 2 = 0. Factoring the left side yields (x – 1)(x – 2) = 0. Setting each factor to 0 yields x – 1 = 0 and x – 2 = 0. Solving for x yields x = 1 or 2.
Also, we have the equation x2 – 4x + 3 = 0. Factoring the left side yields (x – 1)(x – 3) = 0. Setting each factor to 0 yields x – 1 = 0 and x – 3 = 0. Solving for x yields x = 1 or 3.
The common solution of the two equations is x = 1. Hence, (x – 3)2 = (1 – 3)2 = (–2)2 = 4. The answer is (E).
Method II:
Subtracting the equation x2 – 4x + 3 = 0 from the equation x2 – 3x + 2 = 0 yields
x2 – 3x + 2 – (x2 – 4x + 3) = 0
x2 – 3x + 2 – x2 + 4x – 3 = 0
x – 1 = 0
x = 1
Hence, (x = 3)2 = (1 – 3)2 = (–2)2 = 4. The answer is (E).
22. The given equation is
42.42 = k(14 + 7/50)
42.42 = k(14 + 14/100)
42.42 = k(14+ 0.14)
42.42 = k(14.14)
42.42/14.14 = k
3 = k
The answer is (C).
23. We have that |2x–4| = 2. Since |2x = 4| is only the positive value of 2x – 4, the expression 2x – 4 could equal 2 or –2. If 2x – 4 equals 2, x equals 3; and if 2x – 4 equals –2, x equals 1. We also have that (x – 3)2 is equal to 4. By square rooting, we have that x – 3 may equal 2 (Here, x = 3 + 2 = 5), or x – 3 equals –2(Here, x = 3 – 2 = 1). The common solution is x = 1. Hence, the answer is (A).
24. We are given that a >0 and (a + 2)(a – 3)(a + 4) = 0. Hence, the possible solutions are
a + 2 = 0; a = –2, a is not greater than 0, so reject.
a – 3 = 0; a = 3, a is greater than 0, so accept.
a + 4 = 0; a = –4, a is not greater than 0, so reject.
The answer is (C).
25. We are given the system of equations:
x + y = 7
x2 + y2 = 25
Solving the top equation for y yields y = 7 – x. Substituting this into the bottom equation yields
x2 + (7 – x)2 = 25
x2 + 49 – 14x + x2 = 25
2x2 – 14x + 24 = 0
x2 – 7x + 12 = 0
(x – 3)(x – 4) = 0
x – 3 = 0 or x – 4 = 0
x = 3 or x = 4
If x = 3, then y = 7 – 3 = 4. If x = 4, then y = 7 – 4 = 3. In either case, x3 + y3 = 33 + 43 = 27 + 64 = 91. The answer is (E).
26. The given system of equations is
x + l = 6
x – m = 5
x + p = 4
x – q = 3
Subtracting the second equation from the first one yields
(x + l) – (x – m) = 6 – 5
l + m = 1 . . .(1)
Subtracting the fourth equation from the third one yields
(x + p) – (x – q) = 4 – 3
p + q = 1 . . .(2)
Adding equations (1) and (2) yields
(l + m) + (p + q) = 1 + 1 = 2.
l + m + P + q = 2
The answer is (A).
27. We are given the two equations l/m + 1/n = 4/3 and mn = 3. From the second equation, we have n = 3/m. Substituting this in the equation l/m + 1/n = 4/3 yields 1/m + m/3 = 4/3. Multiplying the equation by 3m yields m2 – 4m + 3 = 0. The two possible solutions of this equation are 1 and 3.
Whens m = 1, n = 3/m = 3/1 = 3 and the expression 0.1 + 0.11/m + 0.11/n equals 0.1 + 0.11/1 + 0.11/3; and when m = 3, n = 3/m = 3/3 = 1 and the expression 0.1 + 0.11/m + 0.11/n equals 0.1 + 0.11/3 + 0.11/1.
In either case, the expressions equal 0.1 + 0.11/3 + 0.11/1 = 0.2 + 0.11/3. Hence, the answer is (A).
28. Let each expression in the equation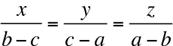 
equal k. Then we have
Simplifying yields
x = k(b – c) = kb – kc
y = k(c – a) – kc – ka
z = k(a – b) = ka – kb
Hence, x + y + z = (kb – kc) + (kc – ka) + (ka – kb) = 0. The answer is (A).
Very Hard
29. We are given three equations ax = b, by = c, and cz = a. From the first equation, we have b = ax. Substituting this in the second equation gives (ax)y = c. We can replace a in this equation with cz (according to the third equation cz = a):
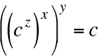
cxyz = c1 |
By multiplying the exponents and writing c as c1 |
xyz = 1 |
By equating the exponents of c on both sides |
The answer is (B).
