Exponents & Roots
EXPONENTS
Exponents afford a convenient way of expressing long products of the same number. The expression bn is called a power and it stands for b × b × b ×…×b, where there are n factors of b. b is called the base, and n is called the exponent. By definition, b0 = 1.*
There are six rules that govern the behavior of exponents:
Rule 1: xa · xb = xa+b |
Example, 23 · 22 = 23+2 = 25 = 32. Caution, xa + xb ≠ xa+b |
Rule 2: (xa)b = xab |
Example, (23)2 = 23 · 2 = 26 = 64 |
Rule 3: (xy)a = xa · ya |
Example, (2y)3 = 23 · y3 = 8y3 |
Rule 4: 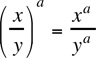 |
Example, 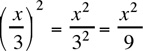 |
Rule 5: 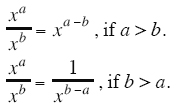 |
Example, 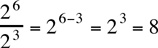 |
|
Example, 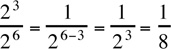 |
Rule 6: 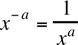 |
Example, 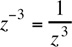 Caution, a negative exponent does not make the number negative; it merely indicates that the base should be reciprocated. For example, Caution, a negative exponent does not make the number negative; it merely indicates that the base should be reciprocated. For example, 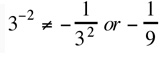 |
Problems involving these six rules are common on the GRE, and they are often listed as hard problems. However, the process of solving these problems is quite mechanical: simply apply the six rules until they can no longer be applied.
Example 1: If x≠0, 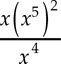 =
=
(A) x5
(B) x6
(C) x7
(D) x8
(E) x9
First, apply the rule (xa)b = xab to the expression 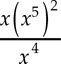 :
:
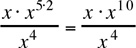
Next, apply the rule xa · xb = xa+b:
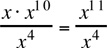
Finally, apply the rule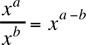 :
:
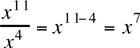
The answer is (C).
Note: Typically, there are many ways of solving these types of problems. For this example, we could have begun with Rule 5, 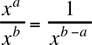 :
:
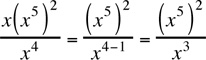
Then apply Rule 2, (xa)b = xab:
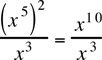
Finally, apply the other version of Rule 5,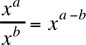
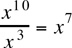
Example 2:
Column A |
Column B |
|
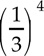
|
Canceling the common factor 3 in Column A yields 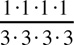 , or
, or 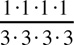 . Now, by the definition of a power,
. Now, by the definition of a power, 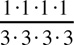 =
= 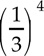 Hence, the columns are equal and the answer is (C).
Hence, the columns are equal and the answer is (C).
Example 3:
Column A |
Column B |
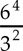
|
24 · 32 |
First, factor Column A: |
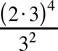
|
Next, apply the rule (xy)a = xa · ya |
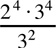
|
Finally, apply the rule 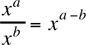 |
24 · 32 |
Hence, the columns are equal and the answer is (C).
ROOTS
The symbol 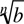 is read the nth root of b, where n is called the index, b is called the base, and
is read the nth root of b, where n is called the index, b is called the base, and 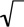 is called the radical,
is called the radical, 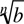 denotes that number which raised to the nth power yields b. In other words, a is the nth root of b if an = b. For example,
denotes that number which raised to the nth power yields b. In other words, a is the nth root of b if an = b. For example, 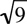 = 3* because 32 = 9, and
= 3* because 32 = 9, and 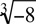 = -2 because (-2)3 = -8. Even roots occur in pairs: both a positive root and a negative root. For example,
= -2 because (-2)3 = -8. Even roots occur in pairs: both a positive root and a negative root. For example, 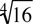 = 2 since 2 = 16, and
= 2 since 2 = 16, and 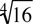 = -2 since (-2)4 = 16. Odd roots occur alone and have the same sign as the base:
= -2 since (-2)4 = 16. Odd roots occur alone and have the same sign as the base: 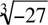 = -3 since (-3) = -27. If given an even root, you are to assume it is the positive root. However, if you introduce even roots by solving an equation, then you must consider both the positive and negative roots:
= -3 since (-3) = -27. If given an even root, you are to assume it is the positive root. However, if you introduce even roots by solving an equation, then you must consider both the positive and negative roots:
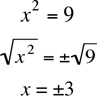
Square roots and cube roots can be simplified by removing perfect squares and perfect cubes, respectively. For example,
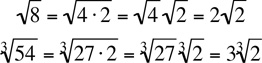
Radicals are often written with fractional exponents. The expression 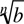 can be written as b1/n. This can be generalized as follows:
can be written as b1/n. This can be generalized as follows:
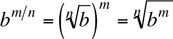
Usually, the form 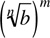 is better when calculating because the part under the radical is smaller in this case. For example,
is better when calculating because the part under the radical is smaller in this case. For example, 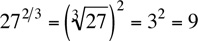 . Using the form
. Using the form 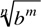 would be much harder in this case:
would be much harder in this case: 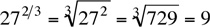 . Most students know the value of
. Most students know the value of 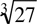 , but few know the value of
, but few know the value of 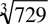 .
.
If n is even, then
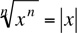
For example, 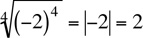 . With odd roots, the absolute value symbol is not needed. For example,
. With odd roots, the absolute value symbol is not needed. For example, 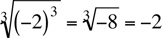 .
.
To solve radical equations, just apply the rules of exponents to undo the radicals. For example, to solve the radical equation x2/3 = 4, we cube both sides to eliminate the cube root:
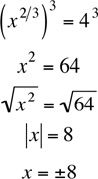
Even roots of negative numbers do not appear on the GRE. For example, you will not see expressions of the form 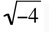 ; expressions of this type are called complex numbers.
; expressions of this type are called complex numbers.
The following rules are useful for manipulating roots:
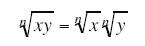
|
For Example, 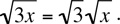 |
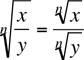
|
For Example, 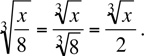 |
Caution: 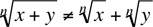 . For example,
. For example, 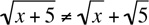 Also,
Also, 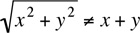 . This common mistake occurs because it is similar to the following valid property:
. This common mistake occurs because it is similar to the following valid property: 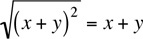 (If x + y can be negative, then it must be written with the absolute value symbol: |x + y|). Note, in the valid formula, it’s the whole term, x + y, that is squared, not the individual x and y.
(If x + y can be negative, then it must be written with the absolute value symbol: |x + y|). Note, in the valid formula, it’s the whole term, x + y, that is squared, not the individual x and y.
To add two roots, both the index and the base must be the same. For example, 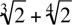 cannot be added because the indices are different, nor can
cannot be added because the indices are different, nor can 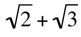 be added because the bases are different. However,
be added because the bases are different. However, 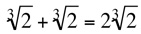 . In this case, the roots can be added because both the indices and bases are the same. Sometimes radicals with different bases can actually be added once they have been simplified to look alike. For example,
. In this case, the roots can be added because both the indices and bases are the same. Sometimes radicals with different bases can actually be added once they have been simplified to look alike. For example, 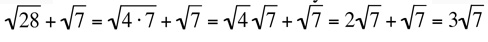 .
.
You need to know the approximations of the following roots: 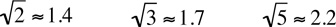
Example 4: Given the system 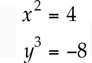 which of the following is NOT necessarily true?
which of the following is NOT necessarily true?
(A) y<0
(B) x<5
(C) y is an integer
(D) x>y
(E)  is an integer
is an integer
y3=-8 yields one cube root, y= -2. However, x2=4 yields two square roots, x = ±2. Now, if x = 2, then x > y; but if x = -2, then x = y. Hence, choice (D) is not necessarily true. The answer is (D).
Example 5: If x < 0 and y is 5 more than the square of x, which one of the following expresses x in terms of y?
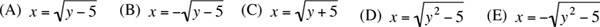
Translating the expression “y is 5 more than the square of x” into an equation yields:
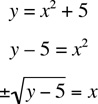
Since we are given that x<0, we take the negative root, 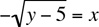 . The answer is (B).
. The answer is (B).
RATIONALIZING
A fraction is not considered simplified until all the radicals have been removed from the denominator. If a denominator contains a single term with a square root, it can be rationalized by multiplying both the numerator and denominator by that square root. If the denominator contains square roots separated by a plus or minus sign, then multiply both the numerator and denominator by the conjugate, which is formed by merely changing the sign between the roots.
Example: Rationalize the fraction 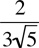
Multiply top and bottom of the fraction by  :
: 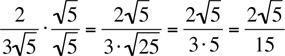
Example: Rationalize the fraction 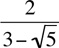 .
.
Multiply top and bottom of the fraction by the conjugate 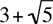
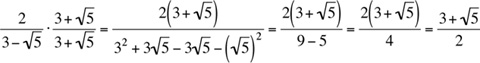
Problem Set R:
 Easy
Easy
1. |
Column A |
|
Column B |
|
x(x2)4 |
|
x(x3)3 |
 Medium
Medium
2. |
Column A |
0 < x < y |
Column B |
|
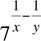
|
|
7x - y |
3. If x = 101.4, y = 100.7, and xz = y3 then what is the value of z?
(A) 0.5
(B) 0.66
(C) 1.5
(D) 2
(E) 3
4. A perfect square is a positive integer which when square rooted results in an integer. If N = 34 · 53 · 7, then what is the biggest perfect square that is a factor of N?
(A) 32
(B) 52
(C) 92
(D) (9 · 5)2
(E) (3 · 5 · 7)2
5. If p = 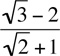 , then which one of the following equals p - 4?
, then which one of the following equals p - 4?
(A) 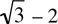
(B) 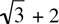
(C) 2
(D) 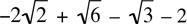
(E) 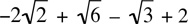
6. 
 Hard
Hard
[Multiple-choice Question - Select One or More Answer Choices]
7. If p = 216-1/3 + 243-2/5 + 256-1/4, then which one of the following is an integer?
(A) p/19
(B) p/36
(C) p
(D) 19/p
(E) 36/p
(F) 19/p
(G) 36p
8. 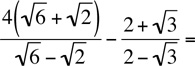
(A) 1
(B) 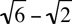
(C) 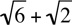
(D) 8
(E) 12
9. If 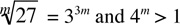 , then what is the value of m?
, then what is the value of m?
(A) -1
(B) -1/4
(C) 0
(D) 1/4
(E) l
10. 
11. If r is negative, which of the following must also be negative?
(A) r2
(B) r3
(C) r4
(D) r2 + r3
(E) r2 · r3
 Very Hard
Very Hard
12. In which one of the following choices must p be greater than q?
(A) 0.9p = 0.9q
(B) O.9p = 0.92q
(C) 0.9p > 0.9q
(D) 9p < 9q
(E) 9p > 9q
Answers and Solutions to Problem Set R
 Easy
Easy
1. Column A: x(x2)4 = x · x2 · 4 = x · x8 = x1+8 = x9.
Column B: (x3)3 = x3 · 3 = x9.
The answer is (C).
 Medium
Medium
2. From the inequality 0 < x < y, x and y are positive and x < y. Hence, the sides of the inequality x < y can be inverted and the direction safely flipped. Hence, l/x > 1/y.
Subtracting y from both sides of the inequality x < y yields x - y < 0.
Finally, subtracting 1/y from both sides of the inequality l/x > 1/y yields l/x - 1/y > 0.
Thus, Column A has 7 raised to a positive number, while Column B has 7 raised to a negative number. Hence, Column A is greater than 1, and Column B is less than 1. The answer is (A).
3. We are given that x= 101.4 and y = 100.7. Substituting these values in the given equation xz = y3 yields
(101.4)z = (100.7)3
101.4z = 100.7 · 3
101.4z = 1021
1.4z = 2.1 since the bases are the same, the exponents must be equal
z = 2.1/1.4 = 3/2
The answer is (C).
4. We are given that N =34 · 53 · 7. Writing N as a product of perfect squares yields (34 · 52) · 5 · 7 = (32 · 5)2 · 5 · 7 = (9 · 5)2 · 5 · 7. The product of the remaining numbers 5 and 7 cannot be written as a perfect square. Hence, (9 · 5)2 is the biggest perfect square factor of N. The answer is (D).
5. Since none of the answers are fractions, let’s rationalize the given fraction by multiplying top and bottom by the conjugate of the bottom of the fraction:
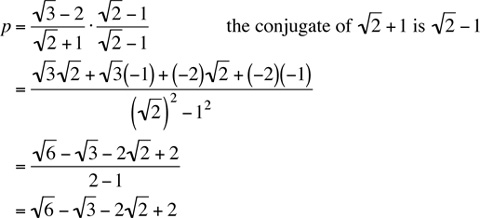
Now, p - 4 = 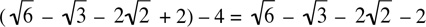 . The answer is (D).
. The answer is (D).
6. Since the columns are positive, we can square both columns without affecting the inequality relation between the columns. Doing this yields

Subtracting 25 from both columns yields

Since  is greater than 0, Column A is greater than Column B. The answer is (A).
is greater than 0, Column A is greater than Column B. The answer is (A).
Method II
Whatever the value of 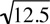 is, it is greater than 3 since
is, it is greater than 3 since 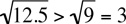 . Hence,
. Hence, 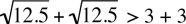 = 6 > 5 = Column B.
= 6 > 5 = Column B.
 Hard
Hard
7. Simplifying the given equation yields

Now,
Choice (A): p/19 = (19/36)/19 = 1/36, not an integer. Reject.
Choice (B): p/36 = (19/36)/36 = 19/362, not an integer. Reject.
Choice (C): p = 19/36, not an integer. Reject.
Choice (D): 19/p = 19/(19/36) = 19 · 36/19 = 36, an integer. Correct.
Choice (E): 36/p = 36/(19/36) = 362/19, not an integer. Reject.
Choice (F): 19p = 19(19/36) = 192/36, not an integer. Reject.
Choice (G): 36p = 36(19/36) = 19, an integer. Accept.
The answer is (D) and (G).
8. Let’s rationalize both fractions by multiplying top and bottom of each fraction by the conjugate of its denominator:
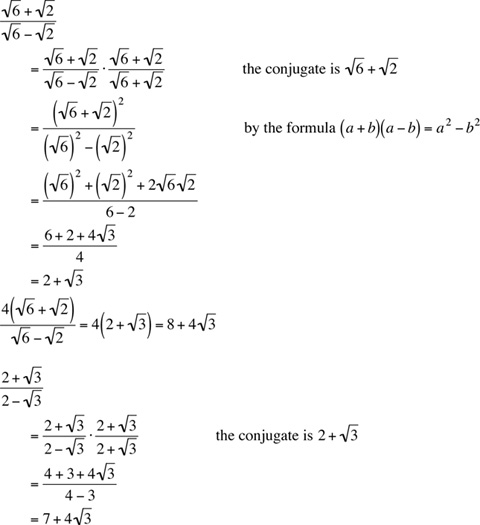
Hence, 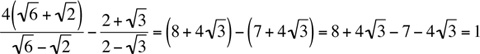 . The answer is (A).
. The answer is (A).
9. We have
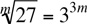
|
|
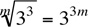
|
By replacing 27 with 33 |
(33)1/m = 33m |
Since by definition 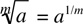 |
33/m = 33m |
Since (xa)b equals xab |
33/m = 3m |
By equating the powers on both sides |
m2 = 1 |
By multiplying both sides by m/3 |
m= ±1 |
By square rooting both sides |
We have 4m > 1. If m = –1, then 4m = 4–1 = 1/4 = 0.25, which is not greater than 1. Hence, m must equal the other value 1. Here, 4m = 41 = 4, which is greater than 1. Hence, m = 1. The answer is (E).
10.
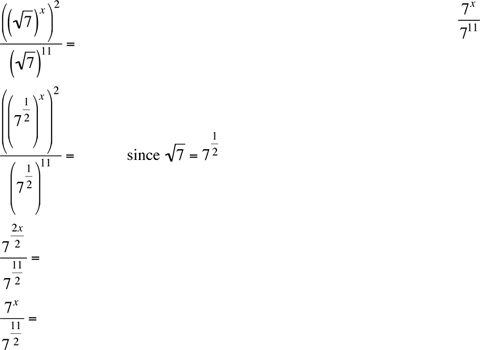
Canceling 7* from both columns yields

Multiplying both columns by 711 · 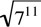 yields
yields
711 |
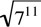
|
Now, clearly, Column A is greater than Column B, and the answer is (A).
11. If r is negative, then r2 and r4 must be positive [Reject (A) and (C)] and r3 and r2 · r3 = r5 must be negative [Accept (B) and (E)]. If r lies between -1 and 0, then r2 is numerically greater than r3 and therefore r2 + r3 is positive. Reject choice (D).
The answer is (B) and (E).
 Very Hard
Very Hard
12. Choice (A): O.9p = 0.9q. Equating exponents on both sides of the equation yields p = q. Hence, p is not greater than q. Reject.
Choice (B): 0.9p = 0.92q. Equating the exponents on both sides yields p = 2q. This is not sufficient information to determine whether p is greater than q. For example, in case both p and q are negative, q > p. In case both p and q are positive, p > p. Hence, reject the choice.
Cases for choices (C), (D), and (E):
A. 0.92>0.93 |
0.81 > 0.729 |
B. 0.91/2 < 0.91/3 |
0.94 < 0.96 |
C. 0.9-2<0.9-3 |
1.1<1.37 |
D. 0.9-1/2 > 0.9-1/31.06 > 1.04 |
|
E. 92<93 |
81 < 729 |
F. 91/2>91/3 |
3 > 2.064 |
G. 9-2>9-3 |
1/81 > 1/729 |
H. 9-1/2 < 9-1/3 |
1/3 < 1/2.06 |
Summary: If ax>ay, then
x > y if a > 1
and
x < y if 0 < a < 1
Choice (C):0.9p > 0.9q:
Comparing the cases A and D against the inequality 0.9p > 0.9q, we have that in A, p (= 2) is less than q (= 3). Hence, reject the choice. In case of D, p (= -1/2) is greater than q (= -1/3).
Choice (D): 9p < 9q:
Comparing the case E against the inequality 9p < 9q, we have that in E, p (= 2) is less than q (= 3). Hence, reject the choice.
Choice (E): 9p > 9q:
The cases F and G match the inequality 9p > 9q. In case of F, p (= 1/2) is greater than q (= 1/3) and also in case G, p(= -2) is greater than q (= -3). In either case, p is greater than q.
The answer is (E).
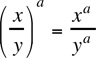
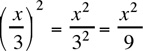
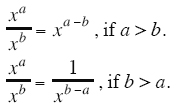
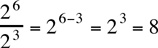
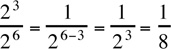
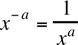
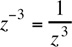 Caution, a negative exponent does not make the number negative; it merely indicates that the base should be reciprocated. For example,
Caution, a negative exponent does not make the number negative; it merely indicates that the base should be reciprocated. For example, 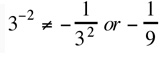
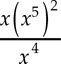 =
=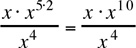
 .
.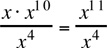
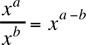 :
: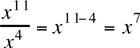
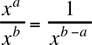 :
: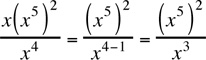
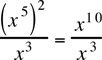
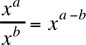
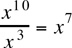
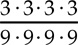
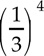
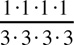 , or
, or 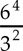
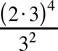
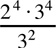
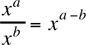
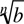 is read the nth root of b, where n is called the index, b is called the base, and
is read the nth root of b, where n is called the index, b is called the base, and 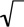 is called the radical,
is called the radical, 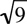 = 3
= 3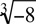 = -2 because (-2)3 = -8. Even roots occur in pairs: both a positive root and a negative root. For example,
= -2 because (-2)3 = -8. Even roots occur in pairs: both a positive root and a negative root. For example, 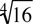 = 2 since 2 = 16, and
= 2 since 2 = 16, and 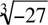 = -3 since (-3) = -27. If given an even root, you are to assume it is the positive root. However, if you introduce even roots by solving an equation, then you
= -3 since (-3) = -27. If given an even root, you are to assume it is the positive root. However, if you introduce even roots by solving an equation, then you 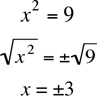
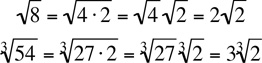
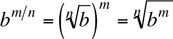
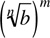 is better when calculating because the part under the radical is smaller in this case. For example,
is better when calculating because the part under the radical is smaller in this case. For example, 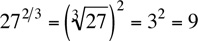 . Using the form
. Using the form 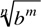 would be much harder in this case:
would be much harder in this case: 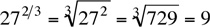 . Most students know the value of
. Most students know the value of 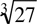 , but few know the value of
, but few know the value of 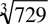 .
.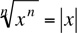
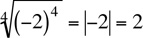 . With odd roots, the absolute value symbol is not needed. For example,
. With odd roots, the absolute value symbol is not needed. For example, 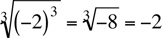 .
.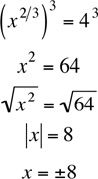
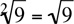 .
.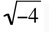 ; expressions of this type are called complex numbers.
; expressions of this type are called complex numbers.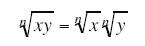
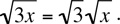
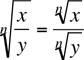
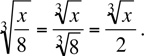
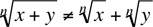 . For example,
. For example, 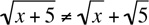 Also,
Also, 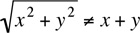 . This common mistake occurs because it is similar to the following valid property:
. This common mistake occurs because it is similar to the following valid property: 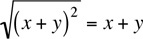 (If x + y can be negative, then it must be written with the absolute value symbol: |x + y|). Note, in the valid formula, it’s the whole term, x + y, that is squared, not the individual x and y.
(If x + y can be negative, then it must be written with the absolute value symbol: |x + y|). Note, in the valid formula, it’s the whole term, x + y, that is squared, not the individual x and y.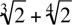 cannot be added because the indices are different, nor can
cannot be added because the indices are different, nor can 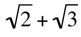 be added because the bases are different. However,
be added because the bases are different. However, 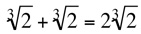 . In this case, the roots can be added because both the indices and bases are the same. Sometimes radicals with different bases can actually be added once they have been simplified to look alike. For example,
. In this case, the roots can be added because both the indices and bases are the same. Sometimes radicals with different bases can actually be added once they have been simplified to look alike. For example, 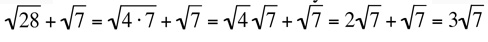 .
.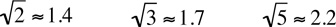
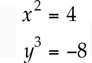 which of the following is NOT necessarily true?
which of the following is NOT necessarily true? is an integer
is an integer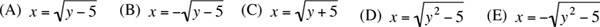
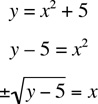
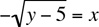 . The answer is (B).
. The answer is (B).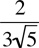
 :
: 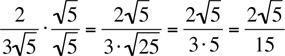
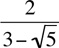 .
.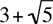
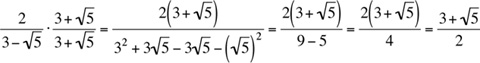
 Easy
Easy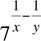
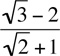 , then which one of the following equals p - 4?
, then which one of the following equals p - 4?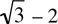
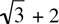
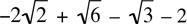
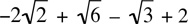

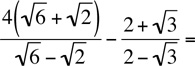
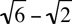
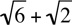
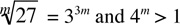 , then what is the value of m?
, then what is the value of m?
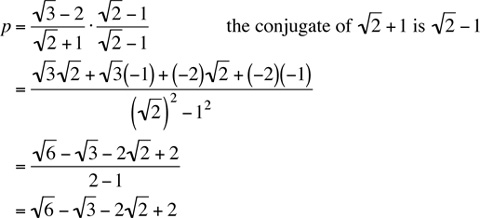
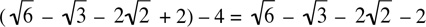 . The answer is (D).
. The answer is (D).

 is greater than 0, Column A is greater than Column B. The answer is (A).
is greater than 0, Column A is greater than Column B. The answer is (A).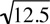 is, it is greater than 3 since
is, it is greater than 3 since 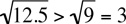 . Hence,
. Hence, 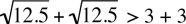 = 6 > 5 = Column B.
= 6 > 5 = Column B.
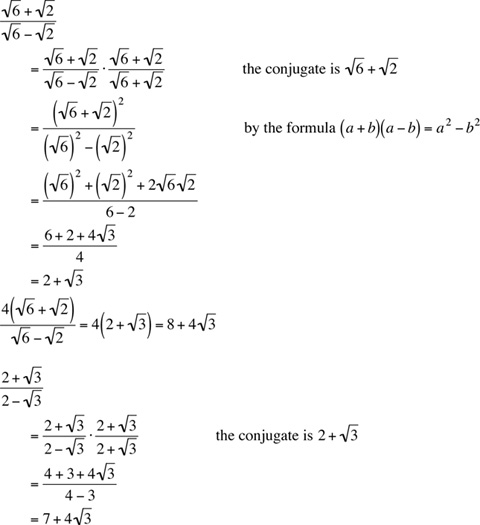
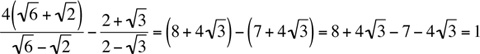 . The answer is (A).
. The answer is (A).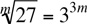
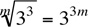
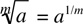
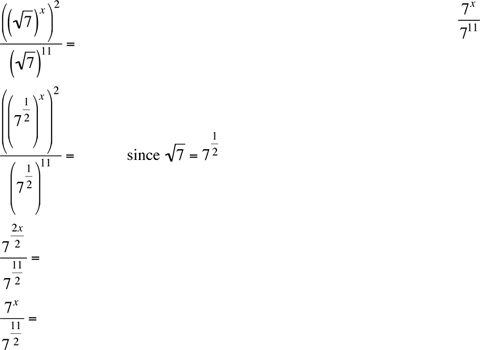

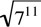 yields
yields