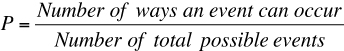
PROBABILITY
We know what probability means, but what is its formal definition? Let’s use our intuition to define it. If there is no chance that an event will occur, then its probability of occurring should be 0. On the other extreme, if an event is certain to occur, then its probability of occurring should be 100%, or 1. Hence, our probability should be a number between 0 and 1, inclusive. But what kind of number? Suppose your favorite actor has a 1 in 3 chance of winning the Oscar for best actor. This can be measured by forming the fraction 1/3. Hence, a probability is a fraction where the top is the number of ways an event can occur and the bottom is the total number of possible events:
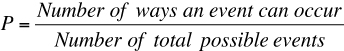
Example: Flipping a coin
What’s the probability of getting heads when flipping a coin?
There is only one way to get heads in a coin toss. Hence, the top of the probability fraction is 1. There are two possible results: heads or tails. Forming the probability fraction gives 1/2.
Example: Tossing a die
What’s the probability of getting a 3 when tossing a die?
A die (a cube) has six faces, numbered 1 through 6. There is only one way to get a 3. Hence, the top of the fraction is 1. There are 6 possible results: 1, 2, 3, 4, 5, and 6. Forming the probability fraction gives 1/6.
Example: Drawing a card from a deck
What’s the probability of getting a king when drawing a card from a deck of cards?
A deck of cards has four kings, so there are 4 ways to get a king. Hence, the top of the fraction is 4. There are 52 total cards in a deck. Forming the probability fraction gives 4/52, which reduces to 1/13. Hence, there is 1 chance in 13 of getting a king.
Example: Drawing marbles from a bowl
What’s the probability of drawing a blue marble from a bowl containing 4 red marbles, 5 blue marbles, and 5 green marbles?
There are five ways of drawing a blue marble. Hence, the top of the fraction is 5. There are 14 (= 4 + 5 + 5) possible results. Forming the probability fraction gives 5/14.
Example: Drawing marbles from a bowl (second drawing)
What’s the probability of drawing a red marble from the same bowl, given that the first marble drawn was blue and was not placed back in the bowl?
There are four ways of drawing a red marble. Hence, the top of the fraction is 4. Since the blue marble from the first drawing was not replaced, there are only 4 blue marbles remaining. Hence, there are 13 (= 4 + 4 + 5) possible results. Forming the probability fraction gives 4/13.
Consecutive Probabilities
What’s the probability of getting heads twice in a row when flipping a coin twice? Previously we calculated the probability for the first flip to be 1/2. Since the second flip is not affected by the first (these are called independent events), its probability is also 1/2. Forming the product yields the probability of two heads in a row: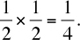 
What’s the probability of drawing a blue marble and then a red marble from a bowl containing 4 red marbles, 5 blue marbles, and 5 green marbles? (Assume that the marbles are not replaced after being selected.) As calculated before, there is a 5/14 likelihood of selecting a blue marble first and a 4/13 likelihood of selecting a red marble second. Forming the product yields the probability of a red marble immediately followed by a blue marble: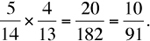 
These two examples can be generalized into the following rule for calculating consecutive probabilities:
To calculate consecutive probabilities, multiply the individual probabilities.
This rule applies to two, three, or any number of consecutive probabilities.
Either-Or Probabilities
What’s the probability of getting either heads or tails when flipping a coin once? Since the only possible outcomes are heads or tails, we expect the probability to be 100%, or 1 :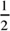 
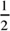+ = 1. Note that the events heads and tails are independent. That is, if heads occurs, then tails cannot (and vice versa).
What’s the probability of drawing a red marble or a green marble from a bowl containing 4 red marbles, 5 blue marbles, and 5 green marbles? There are 4 red marbles out of 14 total marbles. So the probability of selecting a red marble is 4/14 = 2/7. Similarly, the probability of selecting a green marble is 5/14. So the probability of selecting a red or green marble is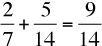 
. Note again that the events are independent. For instance, if a red marble is selected, then neither a blue marble nor a green marble is selected.
These two examples can be generalized into the following rule for calculating either-or probabilities:
To calculate either-or probabilities, add the individual probabilities (only if the events are independent).
The probabilities in the two immediately preceding examples can be calculated more naturally by adding up the events that occur and then dividing by the total number of possible events. For the coin example, we get 2 events (heads or tails) divided by the total number of possible events, 2 (heads and tails): 2/2 = 1. For the marble example, we get 9 (= 4 + 5) ways the event can occur divided by 14 (= 4 + 5 + 5) possible events: 9/14.
If it’s more natural to calculate the either-or probabilities above by adding up the events that occur and then dividing by the total number of possible events, why did we introduce a second way of calculating the probabilities? Because in some cases, you may have to add the individual probabilities. For example, you may be given the individual probabilities of two independent events and be asked for the probability that either could occur. You now know to merely add their individual probabilities.
Geometric Probability
In this type of problem, you will be given two figures, with one inside the other. You’ll then be asked what is the probability that a randomly selected point will be in the smaller figure. These problems are solved with the same principle we have been using: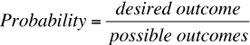 
.
Example: In the figure, the smaller square has sides of length 2 and the larger square has sides of length 4. If a point is chosen at random from the large square, what is the probability that it will be from the small square?
Applying the probability principle, we get Probability =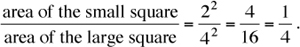 
Statistics is the study of the patterns and relationships of numbers and data. There are four main concepts that may appear on the test:
Median
When a set of numbers is arranged in order of size, the median is the middle number. For example, the median of the set {8, 9, 10, 11, 12} is 10 because it is the middle number. In this case, the median is also the mean (average). But this is usually not the case. For example, the median of the set {8, 9, 10, 11, 17} is 10 because it is the middle number, but the mean is 11 =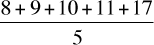 
. If a set contains an even number of elements, then the median is the average of the two middle elements. For example, the median of the set {1, 5, 8, 20} is 
Example: What is the median of 0, –2, 256, 18, 
?
Arranging the numbers from smallest to largest (we could also arrange the numbers from the largest to smallest; the answer would be the same), we get –2, 0, , 18, 256. The median is the middle number, .
Mode
The mode is the number or numbers that appear most frequently in a set. Note that this definition allows a set of numbers to have more than one mode.
Example: What is the mode of 3, –4, 3, 7, 9, 7.5?
The number 3 is the mode because it is the only number that is listed more than once.
Example: What is the mode of 2, π, 2, –9, π, 5?
Both 2 and π are modes because each occurs twice, which is the greatest number of occurrences for any number in the list.
Range
The range is the distance between the smallest and largest numbers in a set. To calculate the range, merely subtract the smallest number from the largest number.
Example: What is the range of 2, 8, 1, –6, π, 1/2?
The largest number in this set is 8, and the smallest number is –6. Hence, the range is 8 – (–6) = 8 + 6 = 14.
Standard Deviation
On the test, you are not expected to know the definition of standard deviation. However, you may be presented with the definition of standard deviation and then be asked a question based on the definition. To make sure we cover all possible bases, we’ll briefly discuss this concept.
Standard deviation measures how far the numbers in a set vary from the set’s mean. If the numbers are scattered far from the set’s mean, then the standard deviation is large. If the numbers are bunched up near the set’s mean, then the standard deviation is small.
Example: Which of the following sets has the larger standard deviation?
A = {1, 2, 3, 4, 5}
B = {1, 4, 15, 21, 27}
All the numbers in Set A are within 2 units of the mean, 3. All the numbers in Set B are greater than 5 units from the mean, 15. Hence, the standard deviation of Set B is greater.
Easy
1. The minimum temperatures from Monday through Sunday in the first week of July in southern Iceland are observed to be –2°C, 4°C, 4°C, 5°C, 7°C, 9°C, 10°C. What is the range of the temperatures?
(A) –10°C
(B) –8°C
(C) 8°C
(D) 10°C
(E) 12°C
Medium
2. What is the probability that the product of two integers (not necessarily different integers) randomly selected from the numbers 1 through 20, inclusive, is odd?
(A) 0
(B) 1/4
(C) 1/2
(D) 2/3
(E) 3/4
3. Two data sets S and R are defined as follows:
Data set S: 28, 30, 25, 28, 27
Dataset R: 22, 19, 15, 17, 21, 25
By how much is the median of data set S greater than the median of data set R
(A) 5
(B) 6
(C) 7
(D) 8
(E) 9
4. If x and y are two positive integers and x + y = 5, then what is the probability that x equals 1?
(A) 1/2
(B) 1/3
(C) 1/4
(D) 1/5
(E) 1/6
5. The following values represent the number of cars owned by the 20 families on Pearl Street.
1, 1, 2, 3, 2, 5, 4, 3, 2, 4, 5, 2, 6, 2, 1, 2, 4, 2, 1, 1
What is the probability that a family randomly selected from Pearl Street has at least 3 cars?
(A) 1/6
(B) 2/5
(C) 9/20
(D) 13/20
(E) 4/5
6. The following frequency distribution shows the number of cars owned by the 20 families on Pearl Street.
|
x |
The number of families having × number of cars |
|
1 |
2 |
|
2 |
2 |
|
3 |
a |
|
4 |
4 |
|
5 |
5 |
|
6 |
2 |
What is the probability that a family randomly selected from the street has at least 4 cars?
(A) 1/10
(B) 1/5
(C) 3/10
(D) 9/20
(E) 11/20
7. Thirty airmail and 40 ordinary envelopes are the only envelopes in a bag. Thirty-five envelopes in the bag are unstamped, and 5/7 of the unstamped envelopes are airmail letters. What is the probability that an envelope picked randomly from the bag is an ordinary airmail envelope?
(A) 1/7
(B) 1/3
(C) 5/14
(D) 17/38
(E) 23/70
8. Set S is the set of all numbers from 1 through 100, inclusive. What is the probability that a number randomly selected from the set is divisible by 3?
(A) 1/9
(B) 33/100
(C) 34/100
(D) 1/3
(E) 66/100
9. What is the probability that the sum of two different numbers randomly picked (without replacement)from the set S = {1, 2, 3, 4} is 5?
(A) 1/5
(B) 3/16
(C) 1/4
(D) 1/3
(E) 1/2
10. The ratio of the number of red balls, to yellow balls, to green balls in a urn is 2 : 3 : 4. What is the probability that a ball chosen at random from the urn is a red ball?
(A) 2/9
(B) 3/9
(C) 4/9
(D) 5/9
(E) 7/9
11. The frequency distribution for x is as given below. What is the range of f?
|
x |
f |
|
0 |
1 |
|
1 |
5 |
|
2 |
4 |
|
3 |
4 |
(A) 0
(B) 1
(C) 3
(D) 4
(E) 5
12. The table shows the distribution of a team of 16 engineers by gender and level.
|
Junior Engineers |
Senior Engineers |
Lead Engineers |
Male |
3 |
4 |
2 |
Female |
2 |
4 |
1 |
If one engineer is selected from the team, what is the probability that the engineer is a male senior engineer?
(A) 7/32
(B) 1/4
(C) 7/16
(D) 1/2
(E) 3/4
13. A prize of $200 is given to anyone who solves a hacker puzzle independently. The probability that Tom will win the prize is 0.6, and the probability that John will win the prize is 0.7. What is the probability that both will win the prize?
(A)0.35
(B)0.36
(C)0.42
(D)0.58
(E)0.88
14. If the probability that Mike will miss at least one of the ten jobs assigned to him is 0.55, then what is the probability that he will do all ten jobs?
(A) 0.1
(B) 0.45
(C) 0.55
(D) 0.85
(E) 1
15. The probability that Tom will win the Booker prize is 0.5, and the probability that John will win the Booker prize is 0.4. There is only one Booker prize to win. What is the probability that at least one of them wins the prize?
(A) 0.2
(B) 0.4
(C) 0.7
(D) 0.8
(E) 0.9
16. The following values represent the exact number of cars owned by the 20 families on Pearl Street.
1, 1, 2, 3, 2, 5, 4, 3, 2, 4, 5, 2, 6, 2, 1, 2, 4, 2, 1, 1
This can be expressed in frequency distribution format as follows:
|
x |
The number of families having x number of cars |
|
1 |
5 |
|
2 |
7 |
|
3 |
a |
|
4 |
3 |
|
5 |
b |
|
6 |
1 |
What are the values of a and b, respectively
(A) 1 and 1
(B) 1 and 2
(C) 1 and 1
(D) 2 and 2
(E) 2 and 3
17. |
Column A |
In a box of 5 eggs, 2 are rotten. |
Column B |
|
The probability that one egg chosen at random from the box is rotten |
|
The probability that two eggs chosen at random from the box are rotten |
Hard
18. A meeting is attended by 750 professionals. 450 of the attendees are females. Half the female attendees are less than thirty years old, and one-fourth of the male attendees are less than thirty years old. If one of the attendees of the meeting is selected at random to receive a prize, what is the probability that the person selected is less than thirty years old?
(A) 1/8
(B) 1/2
(C) 3/8
(D) 2/5
(E) 3/4
[Multiple-choice Question – Select One or More Answer Choices]
19. Removing which of the following numbers from the set S = {1, 2, 3, 4, 5, 6} would move the median of the set S to the right on the number line?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
(F) 6
20. A national math examination has 4 statistics problems. The distribution of the number of students who answered the questions correctly is shown in the chart. If 400 students took the exam and each question was worth 25 points, then what is the average score of the students taking the exam?
|
Question Number |
Number of students who solved the question |
|
1 |
200 |
|
2 |
304 |
|
3 |
350 |
|
4 |
250 |
(A) 1 point
(B) 25 point
(C) 26 point
(D) 69 point
(E) 263.5 point
Very Hard
21. There are 58 balls in a jar. Each ball is painted with at least one of two colors, red or green. It is observed that 2/7 of the balls that have red color also have green color, while 3/7 of the balls that have green color also have red color. What is the probability that a ball randomly picked from the jar will have both red and green colors?
(A) 6/14
(B) 2/7
(C) 6/35
(D) 6/29
(E) 6/42
Answers and Solutions to Problem Set Z
Easy
1. The range is the greatest measurement minus the smallest measurement. The greatest of the seven temperature measurements is 10°C, and the smallest is –2°C. Hence, the required range is 10 – (–2) = 12°C. The answer is (E).
Medium
2. The product of two integers is odd when both integers are themselves odd. Hence, the probability of the product being odd equals the probability of both numbers being odd. Since there is one odd number in every two numbers (there are 10 odd numbers in the 20 numbers 1 through 20, inclusive), the probability of a number being odd is 1/2. The probability of both numbers being odd (independent case) is 1/2 × 1/2 = 1/4. The answer is (B).
3. The definition of median is “When a set of numbers is arranged in order of size, the median is the middle number. If a set contains an even number of elements, then the median is the average of the two middle elements.”
Data set s (arranged in increasing order of size) is 25, 27, 28, 28, 30. The median of the set is the third number 28.
Data set R (arranged in increasing order of size) is 15, 17, 19, 21, 22, 25. The median is the average of the two middle numbers (the 3rd and 4th numbers): (19 + 21)/2 = 40/2 = 20.
The difference of 28 and 20 is 8. The answer is (D).
4. The possible positive integer solutions x and y of the equation x + y = 5 are {x, y} = {1, 4}, {2, 3}, {3, 2}, and {4, 1}. Each solution is equally probable. Exactly one of the 4 possible solutions has x equal to 1. Hence, the probability that x equals 1 is one in four ways, which equals 1/4. The answer is (C).
5. From the distribution given, the 4th, 6th, 7th, 8th, 10th, 11th, 13th, and 17th families, a total of 8, have at least 3 cars. Hence, the probability of selecting a family having at least 3 cars out of the available 20 families is 8/20, which reduces to 2/5. The answer is (B).
6. From the distribution given, there are
4 families having exactly 4 cars
5 families having exactly 5 cars
2 families having exactly 6 cars
Hence, there are 4 + 5 + 2 = 11 families with at least 4 cars. Hence, the probability of picking one such family from the 20 families is 11/20. The answer is (E).
7. We have that 30 airmail and 40 ordinary envelopes are the only envelopes in the bag. Hence, the total number of envelopes is 30 + 40 = 70. We also have that 35 envelopes in the bag are unstamped, and 5/7 of these envelopes are airmail letters. Now, 5/7 × 35 = 25. So the remaining 35 – 25 = 10 are ordinary unstamped envelopes. Hence, the probability of picking such an envelope from the bag is
(Number of unstamped ordinary envelopes) / (Total number of envelopes) =
10/70 =
1/7
The answer is (A).
8. The count of the numbers 1 through 100, inclusive, is 100.
Now, let 3n represent a number divisible by 3, where n is an integer.
Since we have the numbers from 1 through 100, we have 1 ≤ 3n ≤ 100. Dividing the inequality by 3 yields 1/3 ≤ n ≤ 100/3. The possible values of n are the integer values between 1/3 (≈ 0.33) and 100/3 (≈ 33.33). The possible numbers are 1 through 33, inclusive. The count of these numbers is 33.
Hence, the probability of randomly selecting a number divisible by 3 is 33/100. The answer is (B).
9. The first selection can be done in 4 ways (by selecting any one of the numbers 1, 2, 3, and 4 of the set S). Hence, there are 3 elements remaining in the set. The second number can be selected in 3 ways (by selecting any one of the remaining 3 numbers in the set S). Hence, the total number of ways the selection can be made is 4 × 3 = 12.
The selections that result in the sum 5 are 1 and 4, 4 and 1, 2 and 3, 3 and 2, a total of 4 selections. So, 4 of the 12 possible selections have a sum of 5. Hence, the probability is the fraction 4/12 = 1/3. The answer is (D).
10. Let the number of red balls in the urn be 2k, the number of yellow balls 3k, and the number of green balls 4k, where k is a common factor of the three. Now, the total number of balls in the urn is 2k + 3k + 4k = 9k. Hence, the fraction of red balls from all the balls is 2k/9k = 2/9. This also equals the probability that a ball chosen at random from the urn is a red ball. The answer is (A).
11. The range of f is the greatest value of f minus the smallest value of f: 5 – 1 = 4. The answer is (D).
12. From the distribution table, we know that the team has exactly 4 male senior engineers out of a total of 16 engineers. Hence, the probability of selecting a male senior engineer is 4/16 = 1/4. The answer is (B).
13. Let P(A) = The probability of Tom solving the problem = 0.6, and let P(B) = The probability of John solving the problem = 0.7. Now, since events A and B are independent (Tom’s performance is independent of John’s performance and vice versa), we have
P(A and B) =
P(A) × P(B) =
0.6 × 0.7 =
0.42
The answer is (C).
14. There are only two cases:
1) Mike will miss at least one of the ten jobs.
2) Mike will not miss any of the ten jobs.
Hence, (The probability that Mike will miss at least one of the ten jobs) + (The probability that he will not miss any job) = 1. Since the probability that Mike will miss at least one of the ten jobs is 0.55, this equation becomes
0.55 + (The probability that he will not miss any job) = 1
(The probability that he will not miss any job) = 1 – 0.55
(The probability that he will not miss any job) = 0.45
The answer is (B).
15. Probability of Tom winning the prize is 0.5. Hence, probability of Tom not winning is 1 – 0.5 = 0.5.
Probability of John winning is 0.4. Hence, probability of John not winning is 1 – 0.4 = 0.6.
So, the probability of both Tom and John not winning equals
Probability of Tom not winning × Probability of John not winning =
0.5 × 0.6 =
0.3
The probability of one of them (at least) winning + The probability of neither winning = 1 (because these are the only cases.)
Hence, The probability of one of them (at least) not winning = 1 – The probability of neither winning = 1 – 0.3 = 0.7.
The answer is (C).
16. In the frequency distribution table, the first column represents the number of cars and the second column represents the number of families having the particular number of cars. Now, from the data given, the number of families having exactly 3 cars is 2, and the number of families having exactly 5 cars is 2. Hence, a = 2 and b = 2. The answer is (D).
17. Since 2 of the 5 eggs are rotten, the chance of selecting a rotten egg the first time is 2/5. For the second selection, there is only one rotten egg, out of the 4 remaining eggs. Hence, there is a 1/4 chance of selecting a rotten egg again. Hence, the probability of selecting 2 rotten eggs in a row is 2/5 × 1/4 = 1/10. Since 2/5 > 1/10, Column A is greater than Column B. The answer is (A).
Hard
18. The number of attendees at the meeting is 750 of which 450 are female. Hence, the number of male attendees is 750 – 450 = 300. Half of the female attendees are less than 30 years old. One half of 450 is 450/2 = 225. Also, one-fourth of the male attendees are less than 30 years old. One-fourth of 300 is 300/4 = 75.
Now, the total number of (male and female) attendees who are less than 30 years old is 225 + 75 = 300.
So, out of the total 750 attendees 300 attendees are less than 30 years old. Hence, the probability of randomly selecting an attendee less than 30 years old (equals the fraction of all the attendees who are less than 30 years old) is 300/750 = 2/5. The answer is (D).
19. The median of the set S = {1, 2, 3, 4, 5, 6} is half the sum of the middle numbers: (3 + 4)/2 = 7/2 = 3.5.
To move the median to the right on the number line, remove one of the elements to the left of the median on the number line.
For example, removing 3 from the set yields S = {1, 2, 4, 5, 6}. Now, the median is 4; it increased.
The correct answers are the numbers to the left of 3.5 on the number line, choices (A), (B), and (C).
20. The average score of the students is equal to the net score of all the students divided by the number of students. The number of students is 400 (given). Now, let’s calculate the net score. Each question carries 25 points, the first question is solved by 200 students, the second one by 304 students, the third one by 350 students, and the fourth one by 200 students. Hence, the net score of all the students is
200 × 25 + 304 × 25 + 350 × 25 + 250 × 25 =
25(200 + 304 + 350 + 250) =
25(1104)
Hence, the average score equals
25(1104)/400 =
1104/16 =
69
The answer is (D).
Very Hard
21. Let T be the total number of balls, R the number of balls having red color, G the number having green color, and B the number having both colors.
Hence, the number of balls having only red is R – B, the number having only green is G – B, and the number having both is B. Now, the total number of balls is T = (R – B) + (G – B) + B = R + G – B.
We are given that 2/7 of the balls having red color have green also. This implies that B = 2R/7. Also, we are given that 3/7 of the green balls have red color. This implies that B = 3G/7. Solving for R and G in these two equations yields R = 7B/2 and G = 7B/3. Substituting this into the equation T = R + G – B yields T = 7B/2 + 7B/3 – B. Solving for B yields B = 6T/29. Hence, the probability of selecting such a ball is the fraction (6T/29)/T = 6/29. The answer is (D).