Repetition problems have the objects repeating in the combinations or permutations that are formed from a base set.Suppose you must seat 3 of 5 delegates in 3 chairs. And suppose you are interested in the order in which they sit. You will first select 3 of the 5 delegates, and then choose the order in which they sit. The first act is a combination, the second is a permutation. Effectively, the permutation comes after the combination. The delegates in each combination can be ordered in different ways, which can be called permutations of the combination.
Now, if you can select 3 of the 5 delegates in m ways and each selection can be ordered in n ways, then the total number of possible arrangements (permutations) is m · n.
Now, let’s count the number of permutations of 3 objects taken from a set of 4 objects {A, B, C, D}. Let’s call the set {A, B, C, D} a base set.
We must first choose 3 objects from the base set, which yields the following selections:
{A, B, C}, {B, C, D}, {A, C, D}, {A, B, D}
These are combinations. We have 4 selections (combinations) here.
If {El, E2, E3} represents one of the four combinations above, then the following are its possible permutations:
E1 E2 E3
E1 E3 E2
E2 E1 E3
E2 E3 E1
E3 E1 E2
E3 E2 El
You can use this scheme to find the permutations of each of the 4 selections (combinations) we formed above. For example, for the selection {A, B, C}, the following are the six permutations:
A – B – C
A – C – B
B – A – C
B – C – A
C – A – B
C – B – A
Thus, we have 6 permutations for each selection. For practice, you may wish to list the permutations for the remaining 3 selections: {B, C, D}, {A, C, D}, and {A, B, D}.
Summary:
Here, {A, B, C, D} is the base set. We formed 4 combinations that use 3 elements each. Then we formed 6 permutations for each of the 4 combinations. Hence, the problem has in total 6 + 6 + 6 + 6 = 4 × 6 = 24 permutations.
Note 1: A combination might have multiple permutations. The reverse is never true.
Note 2: A permutation is an ordered combination.
Note 3: With combinations, AB = BA. With permutations, AB ≠ BA.
Combinations and their Permutations
Here is another discussion of the distinction between permutations and combinations. The concept is repeated here because it forms the basis for the rest of the chapter.
Combinations are the selections (subsets) of a base set.
For example, the possible combinations of two elements each of the set {A, B} are
A, B or B, A
(Both are the same combination)
The permutations (the combination ordered in different ways) of the combination are
A – B and B – A
(The permutations are different)
How to distinguish between a Combination and a Permutation
At the risk of redundancy, here is yet another discussion of the distinction between permutations and combinations.
As combinations, {A, B, C} and {B, A, C} are the same because each has the same number of each type of object: A, B, and C as in the base set.
But, as permutations, A – B – C and B – A – C are not the same because the ordering is different, though each has the same number of each type of object: A, B, and C as in the base set In fact, no two arrangements that are not identical are ever the same permutation.
Hence, with combinations, look for selections, while with permutations, look for arrangements.
The following definitions will help you distinguish between Combinations and Permutations
Permutations are arrangements (order is important) of objects formed from an original set (base set) such that each new arrangement has an order different from the original set. So, the positions of objects is important.
Combinations are sets of objects formed by selecting (order not important) objects from an original set (base set).
To help you remember, think “Permutation … Position.”
Combinations with Repetitions: Permutations with Repetitions
Here, repetition of objects is allowed in selections or the arrangements.
Suppose you have the base set {A, B, C}. Allowing repetitions, the objects can repeat in the combinations (selections).
Hence, the allowed selections of 2 elements are {A, A}, {A, B} or {B, A}, {B, B}, {B, C} or {C, B}, {C, C}, {C, A} or {A, C} in total 6.
The corresponding permutations are
A – A for {A, A}
A – B and B – A for {A, B}
B – B for {B, B}
B – C and C – B for {B, C}
C – C for {C, C}
C – A and A – C for {C, A}
The total number of combinations is 6, and the total number of permutations is 9. We have 3 objects to choose for 2 positions; allowing repetitions, the calculation is 32 = 9.
Note that {A, B} and {B, A} are the same combination because each has an equal number of A’s and B’s.
By allowing repetitions, you can chose the same object more than once and therefore can have the same object occupying different positions.
In general, permutation means “permutation without repetition,” unless stated otherwise.
Indistinguishable Objects
Suppose we replace C in the base set {A, B, C} with A. Then, we have {A, B, A}. Now the A’s in the first and third positions of the set are indistinguishable and make some of the combinations and permutations formed earlier involving C redundant (because some identical combinations and permutations will be formed). Hence, replacing distinguishable objects with indistinguishable ones reduces the number of combinations and permutations.
Combinations (repetition not allowed) with Indistinguishable Objects
Consider the set {A, B, A}. Here, for example, ABA (2 A’s and 1 B as in the base set) is an allowed combination but ABB (containing 2 B’s not as in base set) is not because B occurs only once in the base set.
The corresponding permutations are listed in Table IV.
Permutations (repetition not allowed) with Indistinguishable Objects
The corresponding permutations are listed in Table IV.
Observe that {A, B, C} has permutations ABC, ACB, BAC, BCA, CAB, and CBA (6 permutations); and {A, B, A} has permutations ABA, AAB, BAA, BAA, AAB, and ABA (we crossed out the last three permutations because they are identical to the first three). So, there are 3 permutations.
Combinations (repetition allowed) with Indistinguishable Objects
Again, consider the set {A, B, A}. Here, for example, ABA is an allowed combination and ABB is an allowed combination.
All the allowed permutations are listed in Table III.
Permutations (repetition allowed) with Indistinguishable Objects
The corresponding permutations are listed in Table III.
Summary:
Repetition problems have the objects repeating in the combinations or permutations that are formed from a base set.
Problems with indistinguishable objects, instead, have the objects repeating in the base set itself.
Allowing repetition increases the number of selections (combinations) and therefore the number of permutations.
Using indistinguishable objects in the base set reduces the number of selections (combinations)and the number of permutations.
The base set is {A, B, C}
Permutations with Repetitions allowed. [n = 3, r = 3]
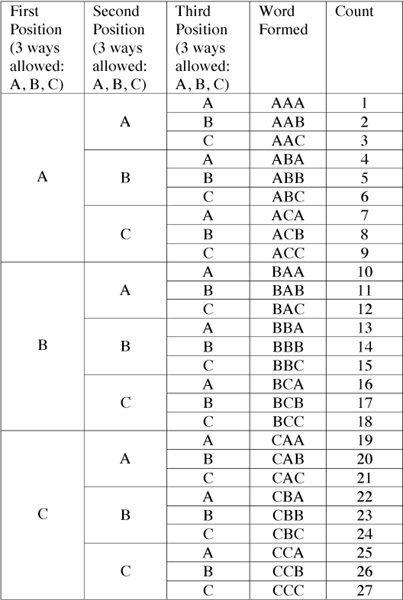
Total number of ways: 27
The base set is {A, B, C}
The Permutations (not allowing Repetitions) are as follows [n = 3, r = 3]. Shaded entries are redundant and therefore not counted. (That is, we pick only the entries in which no object is repeated.) Shaded entries the ones having the same object repeating and therefore not counted.
Total number of ways: 6
There is only 1 combination (without repetition), because any of the 6 words (ABC or ACB or BAC or BCA or CAB or CBA) formed in the above table is the same combination (is a single combination).
Permutations (repetition allowed) using Indistinguishable Objects
By replacing C with A in the base set {A, B, C}, we get {A, B, A}. Reducing the repetitive (redundant) permutations yields
The Permutations (allowing Repetitions) are as follows [n = 3, r = 3], and two of the three objects are indistinguishable. The table is derived by replacing C with A in Table I and eliminating the repeating entries. Shaded entries are redundant and therefore not counted. (That is, we pick only one of the indistinguishable permutations.)
Total number of ways: 8
Permutations (repetition not allowed) with Indistinguishable Objects
Indistinguishable objects are items that repeat in the original set. For example, replace C in the above set with A. Then the new base set would be {A, B, A}. Hence, if we replace C with A in the Table II, we get the repetitions in the permutations. Reducing the repetitive permutations yields
The Permutations (not allowing Repetitions) with Indistinguishable objects are as follows [n = 3, r = 3]. The table is derived by replacing C with A in Table II and eliminating the repeating entries. Shaded entries are redundant and therefore not counted. (That is, we pick only one of the indistinguishable permutations)
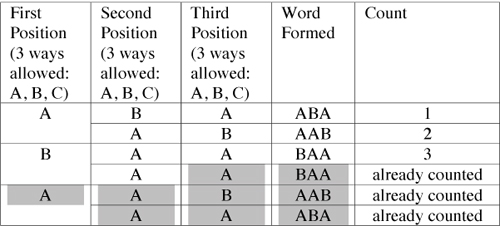
Total number of ways: 3
So far, we have discussed the types of the problems. When trying to solve a problem, it is very helpful to identify its type. Once this is done, we need to count the number of possibilities.
Distinction between Indistinguishable Objects Problems and Repetition Problems
Suppose you are to arrange the letters of the word SUCCESS.
The base set is {S, U, C, C, E, S, S}. There are 3 S’s, which are indistinguishable objects. Hence, the letter S, can be used a maximum of 3 times in forming a new word if repetition is not allowed. So, SSSSUCE is not a possible arrangement.
If repetition is allowed, you can use S as many times as you wish, regardless of the number of S’s in the base word (for example, even if there is only 1 S, you can use it up to maximum allowed times). Hence, SSSSSSS is a possible arrangement.
Counting
There are three models of counting we can use.
We already discussed that if there are m combinations possible from a base set and if there are n permutations possible for each combination, then the total number of permutations possible is m · n.
This is also clear from the Fundamental Principle of Counting.
Model 1:
The Fundamental Principle of Counting:
Construct a tree diagram (we used tables above) to keep track of all possibilities. Each decision made produces a new branch. Finally, count all the allowed possibilities.
The previous tables are examples of tree diagrams. They can represent possibilities as trees. The possibilities are also counted in the tables.
Divide a work into mutually independent jobs and multiply the number of ways of doing each job to find the total number of ways the work can be done. For example, if you are to position three letters in 3 slots, you can divide the work into the jobs as
1) Choose one of three letters A, B, and C for the first position
2) Choose one of the remaining 2 letters for the second position
3) Choose the only remaining letter for the third position
This can be done in 3 × 2 × 1 = 6 ways. The model is a result of the Fundamental Principle of Counting.
Model 3:
Models 1 and 2 are fundamental. Model 3 uses at least one of the first two models. Here, we use the following formula:
Total Number of Permutations = Number of Combinations × Number of Permutations of Each Combination
Predominantly, we use the model for calculating combinations. The total number of permutations and the number of permutations for each combination can be calculated using either or both models 1 and 2 in many cases.
Cyclic Permutations
A cyclic permutation is a permutation that shifts all elements of a given ordered set by a certain amount, with the elements that are shifted off the end inserted back at the beginning in the same order, i.e., cyclically. In other words, a rotation.
For example, {A, B, C, D}, {B, C, D, A}, {C, D, A, B}, and {D, A, B, C} are different linear permutations but the same cyclic permutation. The permutations when arranged in cyclic order, starting from, say, A and moving clockwise, yield the same arrangement {A, B, C, D}. The following figure helps visualize this.
Cyclic arrangements of the cyclic permutations.
For the r placement positions (for the example in the figure, r equals 4), we get r permutations, each is an equivalent cyclic permutation. Hence, the number of cyclic permutations equals
(The number of ordinary permutations) ÷ r
Hence, for nPr permutations, nPr ÷ r cyclic permutations exist. Simply said, r linear permutations would be same cyclic permutation.
Also, {A, B, C, D} and {A, C, B, D} are different linear permutations and different cyclic permutations, because arranging them in cyclic order yields different sequences.
Factorial
The factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n. That is, n! = n(n –1)(n – 2) · · · 3 · 2 · 1. For example, 4! = 4 · 3 · 2 · 1 = 24. Note: 0! is defined to be 1.
Formulas
Verify that the following formulas apply to the scenarios mentioned above. These formulas should be memorized.
Formula 1 : If you have n items to choose from and you choose r of them, then the number of permutations with repetitions allowed is
n · n · … n = nr
(r times)
Formula 2: The formula for permutations with repetitions not allowed is
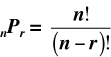
Formula 3: The formula for combinations with repetitions not allowed is
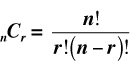
Formula 4: We know that k distinguishable objects have k! different arrangements (permutations). But a set of k indistinguishable objects, will have only 1 indistinguishable permutation. Hence, if we have P permutations for k distinguishable objects, we will have 
permutations for k indistinguishable objects because we now treat the earlier k! arrangements as one.
The case is similar when we have more than one set of indistinguishable objects. Suppose the word ABCDEF has nPr permutations (not allowing repetitions); then the word AAABBC will have 
permutations because here we have a set of 3 indistinguishable objects A and a set of 2 indistinguishable objects B.
There are formulas for the other problem models, but they are not needed for the test. We can always use the Fundamental Principal of Counting for them.
Formula 5: For r linear positions (for the example in the figure, r equals 4), we get r permutations, each of which is an equivalent cyclic permutation. Hence, the number of cyclic permutations is
(The number of ordinary permutations) ÷ r
The formulas in this section will be referenced while we solve the problems.
In permutation and combination problems, it is very important to recognize the type of problem. Many students mistakenly approach a combination problem as a permutation, and vice versa. The steps below will help you determine the problem type.
Solving a permutation or combination problem involves two steps:
1) Recognizing the problem type: permutation vs. combination.
2) Using formulas or models to count the possibilities.
We have three questions to ask ourselves in order to identify the problem type:
1) Is it a permutation or combination?
Check any two typical arrangements with the same combination. If the two arrangements are counted only once, it is a combination problem. Otherwise, it is a permutation.
For example, if you are asked for a lock code, then 321 and 123 could be two possibilities, and the two numbers are formed from the same combination (Same number of 1’s, 2’s, and 3’s). So, lock codes must be permutations.
For another example, suppose you have 5 balls numbering 1 through 5. If you are asked to select 3 out of the 5 balls and you are only interested in the numbers on the balls, not the order in which they are taken, then you have a combination problem.
Problems that by definition connote ordering (though not directly stated) are permutations. For example, 3 digits form a 3-digit number. Here, the 3-digit number connotes ordering. For another example, if you are to answer 3 questions, you probably would not be asked to answer a particular question more than once. So, you would not allow repetition in the calculations. Though not often needed, such logical assumptions are allowed and sometimes expected.
If the problem itself defines slots for the arrangements, it is a permutation problem. Words like “arrange” define slots for the arrangements. We will explain this in more detail later in the problems.
Generally, “arrangements” refer to permutations, and “selections” refer to combinations. These words often flag the problem type.
Other words indicating permutations are “alteration,” “shift,” “transformation,” and “transmutation,” all of which connote ordering.
For example:
In how many ways can the letters of the word XYZ be transformed to form new words?
In how many ways can the letters of the word XYZ be altered to form new words?
Some words indicating combinations are “aggregation,” “alliance,” “association,” “coalition,” “composition,” “confederation,” “gang,” “league,” and “union,” (all of which have nothing to do with arrangements but instead connote selections.)
For example:
In how many ways can a coalition of 2 countries be formed from 4 countries?
(Here, a coalition is the same whether you say country A and B are a coalition or country B and country A are a coalition.)
Check whether, based on the problem description, the results of a permutation/combination can have repetitions.
For example:
If you are to list countries in a coalition, you can hardly list a country twice.
(Here, repetition automatically is not allowed unless specified otherwise.)
If you have 3 doors to a room, you could use the same door for both entering and exiting. (Here, repetition is automatically allowed.)
3) Are there any indistinguishable objects in the base set?
Check the base set: the objects from which a permutation or a combination are drawn. If any indistinguishable objects (repetitions at base set level) are available, collect them. This is easy since it only requires finding identical objects in a base set, which is usually given.
For example, if the original question is to find the words formed from the word GARGUNTUNG, then, in this step, you collect the information: G exists thrice, U exists twice, and so on.
Once the problem type is recognized, use the corresponding formula or model to solve it.
1. There are 3 doors to a lecture room. In how many ways can a lecturer enter and leave the room?
(A) 1
(B) 3
(C) 6
(D) 9
(E) 12
2. There are 3 doors to a lecture room. In how many ways can a lecturer enter the room from one door and leave from another door?
(A) 1
(B) 3
(C) 6
(D) 9
(E) 12
3. How many possible combinations can a 3-digit safe code have?
(A) 9C3
(B) 9P3
(C) 39
(D) 93
(E) 103
4. Goodwin has 3 different colored pants and 2 different colored shirts. In how many ways can he choose a pair of pants and a shirt?
(A) 2
(B) 3
(C) 5
(D) 6
(E) 12
5. In how many ways can 2 doors be selected from 3 doors?
(A) 1
(B) 3
(C) 6
(D) 9
(E) 12
6. In how many ways can 2 doors be selected from 3 doors for entering and leaving a room?
(A) 1
(B) 3
(C) 6
(D) 9
(E) 12
7. In how many ways can a room be entered and exited from the 3 doors to the room?
(A) 1
(B) 3
(C) 6
(D) 9
(E) 12
8. There are 5 doors to a lecture room. Two are red and the others are green. In how many ways can a lecturer enter the room and leave the room from different colored doors?
(A) 1
(B) 3
(C) 6
(D) 9
(E) 12
9. Four pool balls—A, B, C, D—are randomly arranged in a straight line. What is the probability that the order will actually be A, B, C, D?
(A) 1/4
(B)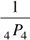 
(C) 
(D) 1/2!
(E) 1/3!
10. A basketball team has 11 players on its roster. Only 5 players can be on the court at one time. How many different groups of 5 players can the team put on the floor?
(A) 511
(B) 11C5
(C) 11P5
(D) 115
(E) 11! · 5!
11. How many different 5-letter words can be formed from the word ORANGE using each letter only once?
(A) 6P6
(B) 36
(C) 6C6
(D) 66
(E) 6P5
12. How many unequal 5-digit numbers can be formed using each digit of the number 11235 only once?
13. How many different six-digit numbers can be formed using all of the following digits:
3, 3, 4, 4, 4, 5
(A) 10
(B) 20
(C) 30
(D) 36
(E) 60
14. This is how Edward’s Lotteries work. First, 9 different numbers are selected. Tickets with exactly 6 of the 9 numbers randomly selected are printed such that no two tickets have the same set of numbers. Finally, the winning ticket is the one containing the 6 numbers drawn from the 9 randomly. There is exactly one winning ticket in the lottery system. How many tickets can the lottery system print?
(A) 9P6
(B) 9P3
(C) 9C9
(D) 9C6
(E) 69
15. How many different strings of letters can be made by reordering the letters of the word SUCCESS?
(A) 20
(B) 30
(C) 40
(D) 60
(E) 420
16. A company produces 8 different types of candies, and sells the candies in gift packs. How many different gift packs containing exactly 3 different candy types can the company put on the market?
(A) 8C2
(B) 8C3
(C) 8P2
(D) 8P3
(E) 
17. Fritz is taking an examination that consists of two parts, A and B, with the following instructions:
Part A contains three questions, and a student must answer two.
Part B contains four questions, and a student must answer two.
Part A must be completed before starting Part B.
In how many ways can the test be completed?
(A) 12
(B) 15
(C) 36
(D) 72
(E) 90
18. A menu offers 2 entrees, 3 main courses, and 3 desserts. How many different combinations of dinner can be made? (A dinner must contain an entrée, a main course, and a dessert.)
(A) 12
(B) 15
(C) 18
(D) 21
(E) 24
19. In how many ways can 3 red marbles, 2 blue marbles, and 5 yellow marbles be placed in a row?
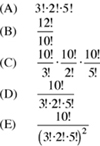
20. The retirement plan for a company allows employees to invest in 10 different mutual funds. Six of the 10 funds grew by at least 10% over the last year. If Sam randomly selected 4 of the 10 funds, what is the probability that 3 of Sam’s 4 funds grew by at least 10% over last year?
21. The retirement plan for a company allows employees to invest in 10 different mutual funds. Six of the 10 funds grew by at least 10% over the last year. If Sam randomly selected 4 of the 10 funds, what is the probability that at least 3 of Sam’s 4 funds grew by at least 10% over the last year?
22. In how many ways can the letters of the word ACUMEN be rearranged such that the vowels always appear together?
23. In how many ways can the letters of the word ACCLAIM be rearranged such that the vowels always appear together?
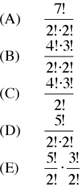
24. In how many ways can the letters of the word GARGANTUNG be rearranged such that all the G’s appear together?
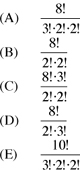
25. In how many ways can the letters of the word GOSSAMERE be rearranged such that all S’s and M’s appear in the middle?
26. How many different four-letter words can be formed (the words need not be meaningful) using the letters of the word GREGARIOUS such that each word starts with G and ends with R?
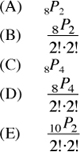
27. A coin is tossed five times. What is the probability that the fourth toss would turn a head?
28. In how many of ways can 5 balls be placed in 4 tins if any number of balls can be placed in any tin?
(A) 5C4
(B) 5P4
(C) 54
(D) 45
(E) 55
29. On average, a sharpshooter hits the target once every 3 shots. What is the probability that he will hit the target in 4 shots?
(A) 1
(B) 1/81
(C) 1/3
(D) 65/81
(E) 71/81
30. On average, a sharpshooter hits the target once every 3 shots. What is the probability that he will not hit the target until 4th shot?
(A) 1
(B) 8/81
(C) 16/81
(D) 65/81
(E) 71/81
31. A new word is to be formed by randomly rearranging the letters of the word ALGEBRA. What is the probability that the new word has consonants occupying only the positions currently occupied by consonants in the word ALGEBRA?
(A) 2/120
(B) 1/24
(C) 1/6
(D) 2/105
(E) 1/35
32. Chelsea has 5 roses and 2 jasmines. A bouquet of 3 flowers is to be formed. In how many ways can it be formed if at least one jasmine must be in the bouquet?
(A) 5
(B) 20
(C) 25
(D) 35
(E) 40
33. In how many ways can 3 boys and 2 girls be selected from a group of 6 boys and 5 girls?
(A) 10
(B) 20
(C) 50
(D) 100
(E) 200
34. In how many ways can a committee of 5 members be formed from 4 women and 6 men such that at least 1 woman is a member of the committee?
(A) 112
(B) 156
(C) 208
(D) 246
(E) 252
35. In how many ways can 5 boys and 4 girls be arranged in a line so that there will be a boy at the beginning and at the end?
36. In how many ways can the letters of the word MAXIMA be arranged such that all vowels are together?
(A) 12
(B) 18
(C) 30
(D) 36
(E) 72
37. In how many ways can the letters of the word MAXIMA be arranged such that all vowels are together and all consonants are together?
(A) 12
(B) 18
(C) 30
(D) 36
(E) 42
38. In how many ways can 4 boys and 4 girls be arranged in a row such that no two boys and no two girls are next to each other?
(A) 1032
(B) 1152
(C) 1254
(D) 1432
(E) 1564
39. In how many ways can 4 boys and 4 girls be arranged in a row such that boys and girls alternate their positions (that is, boy girl boy girl…)?
(A) 1032
(B) 1152
(C) 1254
(D) 1432
(E) 1564
40. The University of Maryland, University of Vermont, and Emory University have each 4 soccer players. If a team of 9 is to be formed with an equal number of players from each university, how many possible teams are there?
(A) 3
(B) 4
(C) 12
(D) 16
(E) 64
41. In how many ways can 5 persons be seated around a circular table?
(A) 5
(B) 24
(C) 25
(D) 30
(E) 120
42. In how many ways can 5 people from a group of 6 people be seated around a circular table?
(A) 56
(B) 80
(C) 100
(D) 120
(E) 144
43. What is the probability that a word formed by randomly rearranging the letters of the word ALGAE is the word ALGAE itself?
(A) 1/120
(B) 1/60
(C) 2/7
(D) 2/5
(E) 1/30
Answers and Solutions to Problem Set AA
1. There are 3 doors to a lecture room. In how many ways can a lecturer enter and leave the room?
(A) 1
(B) 3
(C) 6
(D) 9
(E) 12
Recognizing the Problem:
1) Is it a permutation or a combination problem?
Here, order is important. Suppose A, B, and C are the three doors. Entering by door A and leaving by door B is not the same way as entering by door B and leaving by door A. Hence, AB ≠ BA implies the problem is a permutation (order is important).
2) Are repetitions allowed?
Since the lecturer can enter and exit through the same door, repetition is allowed.
3) Are there any indistinguishable objects in the base set?
Doors are different. They are not indistinguishable, so no indistinguishable objects.
Hence, we have a permutation problem, with repetition allowed and no indistinguishable objects.
Method I (Using known formula for the scenario):
Apply Formula 1, nr, from the Formula section. Here, n = 3, (three doors to choose from), r = 2, 2 slots (one for entry door, one for exit door).
Hence, nr = 32 = 9, and the answer is (D).
Method II (Model 2):
The lecturer can enter the room in 3 ways and exit in 3 ways. So, in total, the lecturer can enter and leave the room in 9 (= 3 · 3) ways. The answer is (D). This problem allows repetition: the lecturer can enter by a door and exit by the same door.
Method III (Model 3):
Let the 3 doors be A, B, and C. We must choose 2 doors: one to enter and one to exit. This can be done in 6 ways: {A, A}, {A, B}, {B, B}, {B, C}, {C, C}, and {C, A}. Now, the order of the elements is important because entering by A and leaving by B is not same as entering by B and leaving by A. Let’s permute the combinations, which yields
A – A
A – B and B – A
{B, B}
B – C and C – B
C – C
C – A and A – C
The total is 9, and the answer is (D).
2. There are 3 doors to a lecture room. In how many ways can a lecturer enter the room from one door and leave from another door?
(A) 1
(B) 3
(C) 6
(D) 9
(E) 12
This problem is the same as the previous one, except entering and leaving must be done by different doors (since the doors are different, repetition is not allowed).
Hence, we have a permutation (there are two slots individually defined: one naming the entering door and one naming the leaving door), without repetition, and no indistinguishable objects (doors are different).
Recognizing the Problem:
1) Is it a permutation or a combination problem?
Here, order is important. Suppose A, B, and C are the three doors. Entering by door B and leaving by door C is not same as entering by door C and leaving by door B. Hence, BC ≠ CB implies the problem is a permutation (order is important).
2) Are repetitions allowed?
We must count the number of possibilities in which the lecturer enters and exits by different doors, so repetition is not allowed.
3) Are there any indistinguishable objects in the base set?
Doors are different. They are not indistinguishable, so no indistinguishable objects.
Hence, we have a permutation problem, with repetition not allowed and no indistinguishable objects.
Method I (Using known formula for the scenario):
Apply Formula 2, nPr, from the Formula section. Here, n = 3 (three doors to choose), r = 2 slots (one for entry door, one for exit door) to place them in.
The calculation is
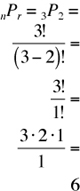
The answer is (C).
Method II (Model 2):
The lecturer can enter the room in 3 ways and exit in 2 ways (not counting the door entered). Hence, in total, the number of ways is 3 · 2 = 6 (by Model 2) or by the Fundamental Principle of Counting 2 + 2 + 2 = 6. The answer is (C). This is a problem with repetition not allowed.
Method III (Model 3):
Let the 3 doors be A, B, and C. Hence, the base set is {A, B, C}. We have to choose 2 doors—one to enter and one to exit. This can be done in 3 ways: {A, B}, {B, C}, {C, A} [The combinations {A, A}, {B, B}, and {C, C} were eliminated because repetition is not allowed]. Now, the order of the permutation is important because entering by A and leaving by B is not considered same as entering by B and leaving by A. Let’s permute the combinations:
{A, B}
{A, C}
{B, A}
{B, C}
{C, A}
{C, B}
The total is 6, and the answer is (C).
3. How many possible combinations can a 3-digit safe code have?
(A) 9C3
(B) 9P3
(C) 39
(D) 93
(E) 103
The safe combination could be 433 or 334; the combinations are the same, but their ordering is different. Since order is important for the safe combinations, this is a permutation problem.
A safe code can be made of any of the numbers {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. No two objects in the set are indistinguishable. Hence, the base set does not have any indistinguishable objects.
Repetitions of numbers in the safe code are possible. For example, 334 is a possible safe code.
Hence, the problem is a permutation, with repetition and no indistinguishable objects. Hence, use Formula 1, nr [here, n = 10, r = 3]. The number of codes is 103 = 1000. The answer is (E).
Safe codes allow 0 to be first digit. Here, the same arrangement rules apply to each of the 3 digits. So, this is a uniform arrangement problem. We can use any formula or model here. But there are non-uniform arrangement problems. For example, if you are to form a 3-digit number, the first digit has an additional rule: it cannot be 0 (because in this case the number would actually be 2-digit number). In such scenarios, we need to use model I or II. The number of ways the digits can be formed by model II is
9 · 10 · 10 = 900
4. Goodwin has 3 different colored pants and 2 different colored shirts. In how many ways can he choose a pair of pants and a shirt?
(A) 2
(B) 3
(C) 5
(D) 6
(E) 12
Model 2:
The pants can be selected in 3 ways and the shirt in 2 ways. Hence, the pair can be selected in 3 · 2 = 6 ways. The answer is (D).
5. In how many ways can 2 doors be selected from 3 doors?
(A) 1
(B) 3
(C) 6
(D) 9
(E) 12
It appears that order is not important in this problem: the doors are mentioned but not defined. Also, since we are selecting doors, it is a combination problem.
The base set is the 3 doors [n = 3]. The doors are different, so there are no indistinguishable objects in the base set.
The arranged sets are the 2 doors [r = 2] we select. A door cannot be selected twice because “we select 2 doors” clearly means 2 different doors.
Hence, the problem is a combination, with no indistinguishable objects and no repetitions. Hence, using Formula 3, nCr, yields
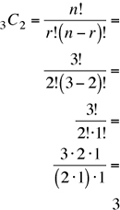
3 The answer is (B).
6. In how many ways can 2 doors be selected from 3 doors for entering and leaving a room?
(A) 1
(B) 3
(C) 6
(D) 9
(E) 12
The problem statement almost ended at “3 doors.” The remaining part “entering and leaving” only explains the reason for the selection. Hence, this does not define the slots. So, this is a combination problem. Moreover, we are asked to select, not to arrange. Hence, the problem is a combination, with no indistinguishable objects and no repetitions allowed. Using Formula 3, the number of ways the room can be entered and left is
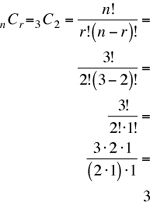
3 The answer is (B).
7. In how many ways can a room be entered and exited from the 3 doors to the room?
(A) 1
(B) 3
(C) 6
(D) 9
(E) 12
There is specific stress on “entered” and “exited” doors. Hence, the problem is not combinational; it is a permutation (order/positioning is important).
The problem type is “no indistinguishable objects and repetitions allowed”. Hence, by Formula 1, the number of ways the room can be entered and exited is nr = 32 = 9. The answer is (D).
8. There are 5 doors to a lecture room. Two are red and the others are green. In how many ways can a lecturer enter the room and leave the room from different colored doors?
(A) 1
(B) 3
(C) 6
(D) 9
(E) 12
There are 2 red and 3 green doors. We have two cases:
The room can be entered from a red door (2 red doors, so 2 ways) and can be left from a green door (3 green doors, so 3 ways): 2 · 3= 6.
The room can be entered from a green door (3 green doors, so 3 ways) and can be left from a red door (2 red doors, so 2 ways): 3 · 2 = 6.
Hence, the total number of ways is
2 · 3 + 3 · 2 = 6 + 6 = 12
The answer is (E).
9. Four pool balls—A, B, C, D—are randomly arranged in a straight line. What is the probability that the order will actually be A, B, C, D?
(A) 1/4
(B) 
(C) 
(D) 1/2!
(E) 1/3!
This is a permutation problem (order is important).
A ball cannot exist in two slots, so repetition is not allowed.
Each ball is given a different identity A, B, C, and D, so there are no indistinguishable objects.
Here, n = 4 (number of balls to arrange) in r = 4 (positions). We know the problem type, and the formula to use. Hence, by Formula 2, the number of arrangements possible is 4P4, and {A, B, C, D} is just one of the arrangements. Hence, the probability is 1 in 4P4, or . The answer is (C).
10. A basketball team has 11 players on its roster. Only 5 players can be on the court at one time. How many different groups of 5 players can the team put on the floor?
(A) 511
(B) 11C5
(C) 11P5
(D) 115
(E) 11! · 5!
The task is only to select a group of 5, not to order them. Hence, this is a combination problem. There are 11 players; repetition is not possible among them (one player cannot be counted more than once); and they are not given the same identity. Hence, there are no indistinguishable objects. Using Formula 3, groups of 5 can be chosen from 11 players in 11C5 ways. The answer is (B).
11. How many different 5-letter words can be formed from the word ORANGE using each letter only once?
(A) 6P3
(B) 36
(C) 6C6
(D) 66
(E) 6P5
In the problem, order is important because ORGAN is a word formed from ORANGE and ORNAG is a word formed from ORANGE, but they are not the same word. Repetition is not allowed, since each letter in the original word is used only once.
The problem does not have indistinguishable objects because no two letters of the word ORANGE are the same. Hence, by Formula 2, nPr, the answer is 6P5, which is choice (E).
12. How many unequal 5-digit numbers can be formed using each digit of the number 11235 only once?
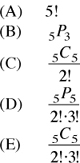
The word “unequal” indicates that this is a permutation problem, because 11532 is the same combination as 11235, but they are not equal. Hence, they are permutations, different arrangements in a combination.
The indistinguishable objects in the base set {1, 1, 2, 3, 5} are the two 1’s.
Since each digit of the number 11235 (objects in the base set) is used only once, repetitions are not allowed.
Hence, by Formula 4, the number of unequal 5-digit numbers that can be formed is
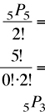
The answer is (B).
13. How many different six-digit numbers can be formed using all of the following digits:
3, 3, 4, 4, 4, 5
(A) 10
(B) 20
(C) 30
(D) 36
(E) 60
Forming a six-digit number is a permutation because the value of the number changes with the different arrangements.
Since we have indistinguishable numbers in the base set, the regular permutations generate repeating numbers. But we are asked for only different six-digit numbers. So, we count only 1 for each similar permutation.
There are two sets of indistinguishable objects in the base set: two 3’s and three 4’s.
No repetitions are allowed since all elements in the base set are to be used in each number.
Hence, by Formula 4, the formula for permutations with no repetitions and with distinguishable objects, the number of six-digit numbers that can be formed is
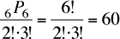
The answer is (E).
14. This is how Edward’s Lotteries work. First, 9 different numbers are selected. Tickets with exactly 6 of the 9 numbers randomly selected are printed such that no two tickets have the same set of numbers. Finally, the winning ticket is the one containing the 6 numbers drawn from the 9 randomly. There is exactly one winning ticket in the lottery system. How many tickets can the lottery system print?
(A) 9P6
(B) 9C3
(C) 9C9
(D) 9C6
(E) 69
The only condition is that the winning ticket has the same set of numbers as the drawn numbers (in whatever order). Hence, order is not important. Now, count the combinations.
Since the numbers in the base set (9 numbers) are different, the base set does not have indistinguishable objects.
Six of the 9 different numbers are selected by the lottery system, so no repetitions are allowed.
By Formula 3, the formula for combinations with no repetitions and no indistinguishable objects, the number of possible selections by the lottery system is 9C6.
Since only one winning ticket (winning combination) exists per lottery system, there is of 9C6 tickets per lottery system. The answer is (D).
15. How many different strings of letters can be made by reordering the letters of the word SUCCESS?
(A) 20
(B) 30
(C) 40
(D) 60
(E) 420
The word SUCCESS is a different word from SUSSECC, while they are the same combination. Hence, this is a permutation problem, not a combination problem.
There are two sets of indistinguishable objects in the base set: 2 C’s and 3 S’s.
Each letter is used only once in each reordering (so do not allow repetition).
Hence, we have a permutation problem, with indistinguishable objects and no repetitions. Using Formula 4, the formula for permutations with no repetitions but with distinguishable objects in the Formula section, yields n = 7 (base word has 7 letters), and r = 1 (each new word will have 7 letters). The repetitions are 2 C’s and 3 S’s. Hence, the total number of permutations is
The answer is (E).
16. A company produces 8 different types of candies, and sells the candies in gift packs. How many different gift packs containing exactly 3 different candy types can the company put on the market?
(A) 8C2
(B) 8C3
(C) 8P2
(D) 8P3
(E)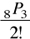 
The phrase “8 different candies” indicates the base set does not have indistinguishable objects.
Since no placement slots are defined, this is a combination problem. We need only to choose 3 of 8 candies; we do not need to order them.
Repetitions are not allowed in the sets formed.
By Formula 3, the formula for permutations with no repetitions but with distinguishable objects yields 8C3 which is Choice (B).
17. Fritz is taking an examination that consists of two parts, A and B, with the following instructions:
Part A contains three questions, and a student must answer two.
Part B contains four questions, and a student must answer two.
Part A must be completed before starting Part B.
In how many ways can the test be completed?
(A) 12
(B) 15
(C) 36
(D) 72
(E) 90
The problem has two parts.
Each part is a permutation problem with no indistinguishable objects (no 2 questions are the same in either part), and repetitions are not allowed (the same question is not answered twice).
Hence, the number of ways of answering the first part is 3P2 (2 questions to answer from 3), and the number of ways of answering the second part is 4P2 (2 questions to answer from 4).
By the Fundamental Principle of Counting, the two parts can be done in
3P2 · 4p2 = 6 · 12 = 72 ways
The answer is (D).
Method II [Model 2]:
The first question in Part A can be chosen to be one of the 3 questions in Part A.
The second question in Part A can be chosen to be one of the remaining 2 questions in Part A.
The first question in Part B can be chosen to be one of the 4 questions in Part B.
The second question in Part B can be chosen to be one of the remaining 3 questions in Part B.
Hence, the number of choices is
3 · 2 · 4 · 3 = 72
The answer is (D).
Method III [Fundamental Principle of Counting combined with Model 2]:
The first question in part A can be chosen to be one of the 3 questions in Part A.
The second question in part A can be chosen to be one of the 3 questions in Part A allowing the repetitions. Hence, number of permutations is 3 · 3 = 9. There are 3 repetitions [Q1 & Q1, Q2 & Q2, Q3 & Q3]. The main question does not allow repetitions since you would not answer the same question again. Deleting them, we have 9 – 3 = 6 ways for Part A.
The first question in Part B can be chosen to be one of the 4 questions in Part B.
The second question in Part B can be chosen to be one of 4 questions in Part B. Hence, the number of permutations is 4 · 4 = 16. There are 4 repetitions [Q1 & Q1, Q2 & Q2, Q3 & Q3, Q4 & Q4]. The main question does not allow repetitions since you would not answer the same question again. Deleting them, we have 16 – 4 = 12 ways for Part A.
Hence, the number of choices is
6 · 12 = 72
The answer is (D).
18. A menu offers 2 entrees, 3 main courses, and 3 desserts. How many different combinations of dinner can be made? (A dinner must contain an entrée, a main course, and a dessert.)
(A) 12
(B) 15
(C) 18
(D) 21
(E) 24
The problem is a mix of 3 combinational problems. The goal is to choose 1 of 2 entrees, then 1 of 3 main courses, then 1 of 3 desserts. The choices can be made in 2, 3, and 3 ways, respectively. Hence, the total number of ways of selecting the combinations is 2 · 3 · 3 = 18. The answer is (C).
We can also count the combinations by the Fundamental Principle of Counting:
|
|
Dessert 1 |
|
Main Course 1 |
Dessert 2 |
|
|
Dessert 3 |
|
|
Dessert 1 |
Entrée 1 |
Main Course 2 |
Dessert 2 |
|
|
Dessert 3 |
|
|
Dessert 1 |
|
Main Course 3 |
Dessert 2 |
|
|
Dessert 3 |
|
|
Dessert 1 |
|
Main Course 1 |
Dessert 2 |
|
|
Dessert 3 |
|
|
Dessert 1 |
Entrée 2 |
Main Course 2 |
Dessert 2 |
|
|
Dessert 3 |
|
|
Dessert 1 |
|
Main Course 3 |
Dessert 2 |
|
|
Dessert 3 |
|
|
Total 18 |
The Fundamental Principle of Counting states:
The total number of possible outcomes of a series of decisions, making selections from various categories, is found by multiplying the number of choices for each decision.
Counting the number of choices in the final column above yields 18.
19. In how many ways can 3 red marbles, 2 blue marbles, and 5 yellow marbles be placed in a row?
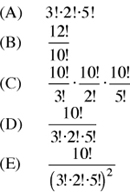
Since the question is asking for the number of ways the marbles can be placed adjacent to each other, this is a permutation problem.
The base set has 3 red marbles (indistinguishable objects), 2 blue marbles (indistinguishable objects) and 5 yellow marbles (indistinguishable objects). The possible arrangements are 3 + 2 + 5 = 10 positions.
The same marble cannot be used twice, so no repetitions are allowed. Formula 4, nPr, and the method for indistinguishable objects (that is, divide the number of permutations, nPr, by the factorial count of each indistinguishable object [see Formulas section]) yield the number of permutations:
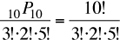
The answer is (D).
20. The retirement plan for a company allows employees to invest in 10 different mutual funds. Six of the 10 funds grew by at least 10% over the last year. If Sam randomly selected 4 of the 10 funds, what is the probability that 3 of Sam’s 4 funds grew by at least 10% over last year?
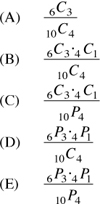
There are 6 winning funds that grew more than 10%, and 4 losing funds that grew less than 10%.
The problem can be split into 3 sub-problems:
We have the specific case where Sam must choose 4 funds, 3 of which are winning, so the remaining fund must be losing. Let’s evaluate the number of ways this can be done. [Note: The order in which the funds are chosen is not important because whether the first 3 funds are winning and the 4th one is losing, or the first fund is losing and the last 3 are winning; only 3 of 4 funds will be winning ones. Hence, this is a combination problem.] The problem has 2 sub-problems:
1. Sam must choose 3 of the 6 winning funds. This can be done in 6C3 ways.
2. Sam must choose one losing fund (say the 4th fund). There are 10 – 6 = 4 losing funds. Hence, the 4th fund can be any one of the 4 losing funds. The selection can be done in 4C1 ways.
Hence, the total number of ways of choosing 3 winning funds and 1 losing one is 6C3 · 4Cl.
3. Sam could have chosen 4 funds in 10C4 ways.
Hence, the probability that 3 of Sam’s 4 funds grew by at least 10% over last year is
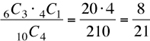
The answer is (B).
21. The retirement plan for a company allows employees to invest in 10 different mutual funds. Six of the 10 funds grew by at least 10% over the last year. If Sam randomly selected 4 of the 10 funds, what is the probability that at least 3 of Sam’s 4 funds grew by at least 10% over the last year?
There are 6 winning funds that grew more than 10%, and 4 losing funds that grew less than 10%.
The problem can be split into 3 sub-problems:
1) Sam has to choose 3 winning funds. This can be done in 6C3 ways.
2) Sam has to choose 1 losing fund. This can be done in 4C1 ways.
Or
3) Sam has to choose all 4 funds to be winning funds. This can be done in 6C4 ways.
This is how Sam chooses at least 3 winning funds.
Hence, the total number of ways of choosing at least 3 winning funds is 6C3 · 4C1 + 6C4.
If there were no restrictions (such as choosing at least 3 winning funds), Sam would have chosen funds in 10C4 ways.
Hence, the probability that at least 3 of Sam’s 4 funds grew by at least 10% over the last year is
The answer is (E).
22. In how many ways can the letters of the word ACUMEN be rearranged such that the vowels always appear together?
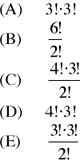
The word “rearranged” indicates that this is a permutation problem.
The base set {A, C, U, M, E, N} has no indistinguishable objects.
Repetition is not allowed.
Since the 3 vowels must appear together, treat the three as an inseparable unit. Hence, reduce the base set to {{A, U, E}, C, M, N}. Now, there are 4 different units in the base set, and they can be arranged in 4P4 = 4! ways. The unit {A, U, E} can itself be internally arranged in 3P3 = 3! ways. Hence, by The Fundamental Principle of Counting, the total number of ways of arranging the word is 4! · 3!. The answer is (D).
23. In how many ways can the letters of the word ACCLAIM be rearranged such that the vowels always appear together?
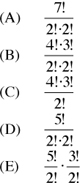
The word “rearranged” indicates that this is a permutation problem.
Since the 3 vowels A, A, and I must appear together, treat the three as an inseparable unit. Hence, reduce the base set to {{A, A, I}, C, C, L, M}.
The set has two indistinguishable objects, C’s.
Also, repetitions are not allowed since we rearrange the word.
Hence, the number of permutations that can be created with units of the set is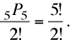 
Now, let’s see how many permutations we can create with the unit {A, A, I}.
The unit {A, A, 1} has two indistinguishable objects, A’s.
Also, repetitions are not allowed.
Hence, by Formula 4, the number of ways of permuting it is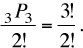 
Hence, by The Fundamental Principle of Counting, the total number of ways of rearranging the letters is
The answer is (E).
24. In how many ways can the letters of the word GARGANTUNG be rearranged such that all the G’s appear together?
The word “rearranged” indicates that this is a permutation problem.
Since all 3 G’s are together, treat them a single inseparable unit. Hence, the base set reduces to {{G, G, G}, A, R, A, N, T, U, N}. There are 8 independent units, 2 A’s (indistinguishable), and two N’s (indistinguishable). No unit is used twice, so there are no repetitions. Hence, by Formula 4, the number of 8! arrangements is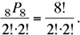 
The 3 G’s can be rearranged amongst themselves in 
way. Hence, the total number of ways the letters can be rearranged is
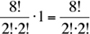
The answer is (B).
25. In how many ways can the letters of the word GOSSAMERE be rearranged such that all S’s and M’s appear in the middle?
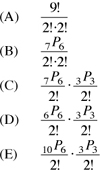
The word “rearranged” indicates that this is a permutation problem.
Since S and M must appear in the middle, treat them as an inseparable unit and reserve the middle seat for them. Correspondingly, bracket them in the base set. The new base set becomes {{S, S, M}, G, O, A, E, R, E}. Hence, we have the following arrangement:
Now, the remaining 6 units G, O, A, E, R, and E can be arranged in the 6 blank slots; and for each arrangement, every permutation inside the unit {S, S, M} is allowed.
Hence, the blank slots can be filled in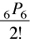 
(E repeats twice) ways.
And the unit {S, S, M} can be internally arranged in 
ways.
Hence, by Model 2, the total number of ways the letters can be rearranged is
The answer is (D).
26. How many different four-letter words can be formed (the words need not be meaningful) using the letters of the word GREGARIOUS such that each word starts with G and ends with R?
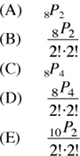
Place one G in the first slot and one R in the last slot:
The remaining letters, {G, R, E, A, I, O, U, S}, can be arranged in the remaining 2 slots in 8P2 (no indistinguishable objects nor repetition). The answer is (A).
Note: Since the two G’s in the base word are indistinguishable, the word G1G2AR is the same as G2G1AR. Hence, the internal arrangement of the G’s or, for the same reason, the R’s is not important.
27. A coin is tossed five times. What is the probability that the fourth toss would turn a head?
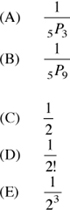
The fourth toss is independent of any other toss. The probability of a toss turning heads is 1 in 2, or simply 1/2. Hence, the probability of the fourth toss being a head is 1/2. The answer is (C).
Each toss has 2 outcomes. Hence, 5 tosses have 2 · 2 · 2 ·… 2 (5 times) = 25 outcomes (permutation with repetition over r = 2 and n = 5 [repetitions allowed: the second and the fourth toss may both yield heads or tails]).
Reserve the third toss for a head. Now, the number of ways the remaining 4 tosses can be tossed is 24 (repetitions allowed). The probability is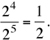 
The answer is (C).
28. In how many of ways can 5 balls be placed in 4 tins if any number of balls can be placed in any tin?
(A) 5C4
(B) 5P4
(C) 54
(D) 45
(E) 55
The first ball can be placed in any one of the four tins.
Similarly, the second, the third, the fourth, and the fifth balls can be placed in any one of the 4 tins.
Hence, the number of ways of placing the balls is 4 · 4 · 4 · 4 · 4 = 45. The answer is (D).
Note: We used Model 2 here.
29. On average, a sharpshooter hits the target once every 3 shots. What is the probability that he will hit the target in 4 shots?
(A) 1
(B) 1/81
(C) 1/3
(D) 65/81
(E) 71/81
The sharpshooter hits the target once in 3 shots. Hence, the probability of hitting the target is 1/3. The probability of not hitting the target is 1 – 1/3 = 2/3.
Now, (the probability of not hitting the target even once in 4 shots) + (the probability of hitting at least once in 4 shots) equals 1, because these are the only possible cases.
Hence, the probability of hitting the target at least once in 4 shots is
1 – (the probability of not hitting even once in 4 shots)
The probability of not hitting in the 4 chances is =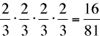 
. Now, 1 – 16/81 = 65/81. The answer is (D).
This methodology is similar to Model 2. You might try analyzing why. Clue: The numerators of 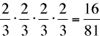are the number of ways of doing the specific jobs, and the denominators are the number of ways of doing all possible jobs.
30. On average, a sharpshooter hits the target once in every 3 shots. What is the probability that he will not hit the target until 4th shot?
(A) 1
(B) 8/81
(C) 16/81
(D) 65/81
(E) 71/81
The sharpshooter hits the target once in 3 shots. Hence, the probability of hitting the target is 1/3. The probability of not hitting the target is 1 – 1/3 = 2/3.
He will not hit the target on the first, second, and third shots, but he will hit it on the fourth shot. The probability of this is
The answer is (B).
This methodology is similar to Model 2. You might try analyzing why. Clue: The numerators of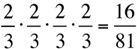 
are the number of ways of doing the specific jobs, and the denominators are the number of ways of doing all possible jobs.
31. A new word is to be formed by randomly rearranging the letters of the word ALGEBRA. What is the probability that the new word has consonants occupying only the positions currently occupied by consonants in the word ALGEBRA?
(A) 2/120
(B) 1/24
(C) 1/6
(D) 2/105
(E) 1/35
If we do not put restrictions on the arrangements of the consonants, then by Formula 4 the number of words that can be formed from the word ALGEBRA is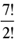 
(A repeats).
If we constrain that the positions of consonants is reserved only for consonants, then the format of the new arrangement should look like this
A, L, G, E, B, R, A
V, C, C, V, C, C, V
V for vowels, C for consonants.
The 4 slots for consonants can be filled in 4P4 = 4! ways, and the 3 slots for vowels can be filled in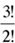 
(A repeats) ways. Hence, by Formula 2, the total number of arrangements in the format is 
.
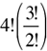Hence, the probability is
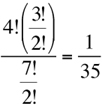
The answer is (E).
32. Chelsea has 5 roses and 2 jasmines. A bouquet of 3 flowers is to be formed. In how many ways can it be formed if at least one jasmine must be in the bouquet?
(A) 5
(B) 20
(C) 25
(D) 35
(E) 40
This is a selection problem because whether you choose a jasmine first or a rose first does not matter.
The 3 flowers in the bouquet can be either 1 jasmine and 2 roses or 2 jasmines and 1 rose.
1 of 2 jasmines can be selected in 2C1 ways.
2 of 5 roses can be selected in 5C2 ways.
The subtotal is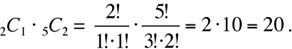 
2 of 2 jasmines can be selected in 2C2 ways.
1 of 5 roses can be selected in 5C1 ways.
The subtotal is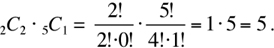 
The grand total is 20 + 5 = 25 ways. The answer is (C).
33. In how many ways can 3 boys and 2 girls be selected from a group of 6 boys and 5 girls?
(A) 10
(B) 20
(C) 50
(D) 100
(E) 200
We have two independent actions to do:
1) Select 3 boys from 6 boys.
2) Select 2 girls from 5 girls.
Selection is a combination problem since selection does not include ordering. Hence, by Model 2, the number of ways is
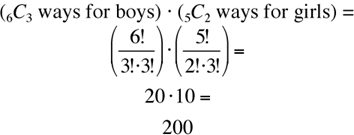
The answer is (E).
34. In how many ways can a committee of 5 members be formed from 4 women and 6 men such that at least 1 woman is a member of the committee?
(A) 112
(B) 156
(C) 208
(D) 246
(E) 252
Forming members of committee is a selection action and therefore this is a combination problem. Whether you select A first and B next or vice versa, it will only be said that A and B are members of the committee.
The number of ways of forming the committee of 5 from 4 + 6 = 10 people is 10C5. The number of ways of forming a committee with no women (5 members to choose from 6 men) is 6C5. Hence, the number of ways of forming the combinations is
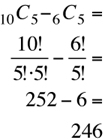
The answer is (D).
35. In how many ways can 5 boys and 4 girls be arranged in a line so that there will be a boy at the beginning and at the end?
The arrangement is a permutation, and there are no indistinguishable objects because no two boys or girls are identical. The first and the last slots hold two of the 5 boys, and the remaining slots are occupied by the 4 girls and the 3 remaining boys.
The first and the last slots can hold 2 of the 5 boys in 5P2 ways, and the 3 boys and the 4 girls position themselves in the middle slots in 7P7 ways. Hence, there are 
possible arrangements. The answer is (C).
36. In how many ways can the letters of the word MAXIMA be arranged such that all vowels are together?
(A) 12
(B) 18
(C) 30
(D) 36
(E) 72
The base set can be formed as {{A, I, A}, M, X, M}. The unit {A, I, A} arranges itself in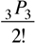 
ways. The 4 units in the base set can be arranged in 4P4/2! ways. Hence, the total number of ways of arranging the letters is
The answer is (D).
37. In how many ways can the letters of the word MAXIMA be arranged such that all vowels are together and all consonants are together?
(A) 12
(B) 18
(C) 30
(D) 36
(E) 42
Since vowels are together and consonants are together, arrange the base set as {{A, I, A}, {M, X, M}} Here, {A, I, A} and {M, X, M} are two inseparable units.
The two units can be mutually arranged in 2P2 ways.
Each unit has 3 objects, 2 of which are indistinguishable.
Hence, the number of permutations of each is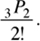
Hence, the total number of arrangements possible is
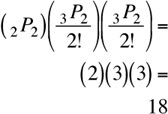
The answer is (B).
38. In how many ways can 4 boys and 4 girls be arranged in a row such that no two boys and no two girls are next to each other?
(A) 1032
(B) 1152
(C) 1254
(D) 1432
(E) 1564
Form the base set as {{B1, B2, B3, B4}, {G1, G2, G3, G4}}; Looking at the problem, either B’s or G’s occupy the odd slots and the other one occupies the even slots. Choosing one to occupy an odd slot set can be done in 2P1 ways, and the other one is automatically filled by the other group.
Now, fill B’s in odd slots (the number of ways is 4P4), and fill G’s in even slots (the number of ways is 4P4 ways). The total number of ways of doing this is 4P4 · 4P4.
The number of ways of doing all of this is 2! · 4P4 · 4P4 = 2 · 24 · 24 = 1152. The answer is (B).
39. In how many ways can 4 boys and 4 girls be arranged in a row such that boys and girls alternate their positions (that is, boy girl)?
(A) 576
(B) 1152
(C) 1254
(D) 1432
(E) 1564
Form the base set as {{B1, B2, B3, B4},{G1, G2, G3, G4}}; the set {B1, B2, B3, B4} occupies alternate positions, as does the set {G1, G2, G3, G4}.
Now there are odd slots and even slots. Each odd slot alternates, and each even slot alternates. Therefore, we have two major slots: even and odd and two units to occupy them: {B1, B2, B3, B4} and {G1, G2, G3, G4}. This can be done in 2P1 ways.
An alternate explanation for this is: The person starting the row can be chosen in 2 ways (i.e., either boys start the first position and arrange alternately or girls start and do the same), either B starts first or G starts first.
Either way, the positions {1, 3, 5, 7} are reserved for one of the two groups B or G. and the positions {2, 4, 6, 8} are reserved for the other group. Arrangements in each position set can be done in 4P4 ways.
Hence, the total number of arrangements is 2! · 4P4 · 4P4 = 2 · 24 · 24 = 1152. The answer is (B).
Mathematically, this problem is the same as the previous one. Just the expression (wording) of the problem is different.
40. The University of Maryland, University of Vermont, and Emory University have each 4 soccer players. If a team of 9 is to be formed with an equal number of players from each university, how many possible teams are there?
(A) 3
(B) 4
(C) 12
(D) 16
(E) 64
The selection from the 3 universities can be done in 4 × 4 × 4 = 43 = 64 ways.
The answer is (E).
41. In how many ways can 5 persons be seated around a circular table?
(A) 5
(B) 24
(C) 25
(D) 30
(E) 120
For a circular table, we use cyclical permutations, not linear permutations. Hence, 1 in every r linear permutations (here n = 5 and r = 5) is a circular permutation. There are 5P5 linear permutations. Hence,
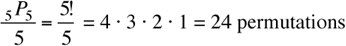
The answer is (B).
42. In how many ways can 5 people from a group of 6 people be seated around a circular table?
(A) 56
(B) 80
(C) 100
(D) 120
(E) 144
For a circular table, we use cyclical permutations, not linear permutations. Hence, 1 in every r linear permutations (here r = 5) is a circular permutation. There are 6P5 linear permutations and therefore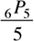 
circular permutations. Now,
The answer is (E).
43. What is the probability that a word formed by randomly rearranging the letters of the word ALGAE is the word ALGAE itself?
(A) 1/120
(B) 1/60
(C) 2/7
(D) 2/5
(E) 1/30
The number of words that can be formed from the word ALGAE is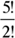 
(A repeats). ALGAE is just one of the words. Hence, the probability is 
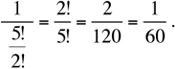The answer is (B).
