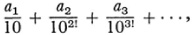
God made the integers; all else is the work of man.
LEOPOLD KRONECKER
One of the most surprising facts in the history of mathematics is that the logical foundation of the real number system was not erected until the late nineteenth century. Up to that time not even the simplest properties of positive and negative rational numbers and irrational numbers were logically established, nor were these numbers defined. Even the logical foundation of complex numbers had not been long in existence (Chap. 32, sec. 1), and that foundation presupposed the real number system. In view of the extensive development of algebra and analysis, all of which utilized the real numbers, the failure to consider the precise structure and properties of the real numbers shows how illogically mathematics progresses. The intuitive understanding of these numbers seemed adequate and mathematicians were content to operate on this basis.
The rigorization of analysis forced the realization that the lack of clarity in the number system itself had to be remedied. For example, Bolzano’s proof (Chap. 40, sec. 2) that a continuous function that is negative for x = a and positive for x = b is zero for some value of x between a and b floundered at a critical point because he lacked an adequate understanding of the structure of the real number system. The closer study of limits also showed the need to understand the real number system, for rational numbers can have an irrational limit and conversely. Cauchy’s inability to prove the sufficiency of his criterion for the convergence of a sequence likewise resulted from his lack of understanding of the structure of the number system. The study of discontinuities of functions representable by Fourier series revealed the same deficiency. It was Weierstrass who first pointed out that to establish carefully the properties of continuous functions he needed the theory of the arithmetic continuum.
Another motivation to erect the foundations of the number system was the desire to secure the truth of mathematics. One consequence of the creation of non-Euclidean geometry was that geometry had lost its status as truth (Chap. 36, sec. 8), but it still seemed that the mathematics built on the ordinary arithmetic must be unquestionable reality in some philosophical sense. As far back as 1817, in his letter to Olbers, Gauss1 had distinguished arithmetic from geometry in that only the former was purely a priori. In his letter to Bessel of April 9, 1830,2 he repeats the assertion that only the laws of arithmetic are necessary and true. However, the foundation of the number system that would dispel any doubts about the truth of arithmetic and of the algebra and analysis built on that base was lacking.
It is very much worth noting that before the mathematicians appreciated that the number system itself must be analyzed, the problem that had seemed most pertinent was to build the foundations of algebra, and in particular to account for the fact that one could use letters to represent real and complex numbers and yet operate with letters by means of properties accepted as true for the positive integers. To Peacock, De Morgan, and Duncan Gregory, algebra in the early nineteenth century was an ingenious but also an ingenuous complex of manipulatory schemes with some rhyme but very little reason ; it seemed to them that the crux of the current confusion lay in the inadequate foundation for algebra. We have already seen how these men resolved this problem (Chap. 32, sec. 1). The late nineteenth-century men realized that they must probe deeper on behalf of analysis and clarify the structure of the entire real number system. As a by-product they would also secure the logical structure of algebra, for it was already intuitively clear that the various types of numbers possessed the same formal properties. Hence if they could establish these properties on a sound foundation, they could apply them to letters that stood for any of these numbers.
A step in the direction of an improved understanding of irrational numbers was the mid-nineteenth-century work on algebraic and transcendental irrationals. The distinction between algebraic and transcendental irrationals had been made in the eighteenth century (Chap. 25, sec. 1). The interest in this distinction was heightened by the nineteenth-century work on the solution of equations, because this work revealed that not all algebraic irrationals could be obtained by algebraic operations on rational numbers. Moreover, the problem of determining whether e and ? were algebraic or transcendental continued to attract mathematicians.
Up to 1844, the question of whether there were any transcendental irrationals was open. In that year Liouville3 showed that any number of the form
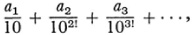
where the ai are arbitrary integers from 0 to 9, is transcendental.
To prove this, Liouville first proved some theorems on the approximation of algebraic irrationals by rational numbers. By definition (Chap. 25, sec. 1) an algebraic number is any number, real or complex, that satisfies an algebraic equation
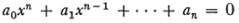
where the ai are integers. A root is said to be an algebraic number of degree n if it satisfies an equation of the nth degree but of no lower degree. Some algebraic numbers are rational; these are of degree one. Liouville proved that if p/q is any approximation to an algebraic irrational x of degree n, with p and q integral, then there exists a positive number M such that
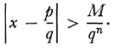
This means that any rational approximation to an algebraic irrational of degree ? by any pjq must be less accurate than M\qn. Alternatively we may say that if ? is an algebraic irrational of degree n, there is a positive number M such that the inequality
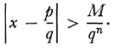
has no solutions in integers p and q for μ = n and hence for μ ⊈ n. Then x is transcendental if for a fixed M and for every positive integer μ the inequality has a solution p/q. By showing that his irrationals satisfy this last criterion, Liouville proved they were transcendental.
The next big step in the recognition of specific transcendental numbers was Hermite’s proof in 18734 that e is transcendental. After obtaining this result, Hermite wrote to Carl Wilhelm Borchardt (1817-80), “I do not dare to attempt to show the transcendence of π. If others undertake it, no one will be happier than I about their success, but believe me, my dear friend, this cannot fail to cost them some effort.”
That π is transcendental had already been suspected by Legendre (Chap. 25, sec. I). Ferdinand Lindemann (l852-1939) proved this in 1882 5 by a method that does not differ essentially from Hermite’s. Lindemann established that if xu x 2,…, xn are distinct algebraic numbers, real or complex, and/)1,/)2,…,ƒ>„ are algebraic numbers and not all zero, then the sum
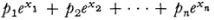
cannot be 0. If we take n = 2, px = 1, and x2 = 0, we see that ex1 cannot be algebraic for an xr that is algebraic and nonzero. Since xx can be 1, « is transcendental. Now it was known that e1x + 1 =0; hence the number in cannot be algebraic. Then π is not, because i is, and the product of two algebraic numbers is algebraic. The proof that π is transcendental disposed of the last point in the famous construction problems of geometry, for all constructible numbers are algebraic.
One mystery about a fundamental constant remains. Euler’s constant (Chap. 20, sec. 4)
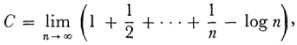
which is approximately 0.577216 and which plays an important role in analysis, notably in the study of the gamma and zeta functions, is not known to be rational or irrational.
By the latter part of the nineteenth century the question of the logical structure of the real number system was faced squarely. The irrational numbers were considered to be the main difficulty. However, the development of the meaning and properties of irrational numbers presupposes the establishment of the rational number system. The various contributors to the theory of irrational numbers either assumed that the rational numbers were so assuredly known that no foundation for them was needed or gave some hastily improvised scheme.
Curiously enough, the erection of a theory of irrationals required not much more than a new point of view. Euclid in Book V of the Elements had treated incommensurable ratios of magnitudes and had defined the equality and inequality of such ratios. His definition of equality (Chap. 4, sec. 5) amounted to dividing the rational numbers m/n into two classes, those for which m/n is less than the incommensurable ratio a/b of the magnitudes a and b and those for which m/n is greater. It is true that Euclid’s logic was deficient because he never defined an incommensurable ratio. Moreover, Euclid’s development of the theory of proportion, the equality of two incommensurable ratios, was applicable only to geometry. Nevertheless, he did have the essential idea that could have been used sooner to define irrational numbers. Actually Dedekind did make use of Euclid’s work and acknowledged this debt;6 Weierstrass too may have been guided by Euclid’s theory. However, hindsight is easier than foresight. The long delay in taking advantage of some reformulation of Euclid’s ideas is readily accounted for. Negative numbers had to be fully accepted so that the complete rational number system would be available. Moreover, the need for a theory of irrationals had to be felt, and this happened only when the arithmetization of analysis had gotten well under way.
In two papers, read before the Royal Irish Academy in 1833 and 1835 and published as “Algebra as the Science of Pure Time,” William R. Hamilton offered the first treatment of irrational numbers.7 He based his notion of all the numbers, rationals and irrationals, on time, an unsatisfactory basis for mathematics (though regarded by many, following Kant, as a basic intuition). After presenting a theory of rational numbers he introduced the idea of partitioning the rationals into two classes (the idea will be described more fully in connection with Dedekind’s work) and defined an irrational number as such a partition. He did not complete the work.
Apart from this unfinished work all pre-Weierstrassian introductions of irrationals used the notion that an irrational is the limit of an infinite sequence of rationals. But the limit, if irrational, does not exist logically until irrationals are defined. Cantor8 points out that this logical error escaped notice for some time because the error did not lead to subsequent difficulties. Weierstrass, in lectures at Berlin beginning in 1859, recognized the need for and gave a theory of irrational numbers. A publication by H. Kossak, Die Elemente der Arithmetik (1872), claimed to present this theory but Weierstrass disowned it.
In 1869 Charles Méray (1835-1911), an apostle of the arithmetization of mathematics and the French counterpart of Weierstrass, gave a definition of the irrationals based on the rationals.9 Georg Cantor also gave a theory, which he needed to clarify the ideas on point sets that he used in his 1871 work on Fourier series. This was followed one year later by the theory of (Heinrich) Eduard Heine, which appeared in the Journal für Mathematik, 10 and one by Dedekind, which he published in Stetigkeit und irrationale Zahlen.11
The various theories of irrational numbers are in essence very much alike; we shall therefore confine ourselves to giving some indication of the
theories of Cantor and Dedekind. Cantor12 starts with the rational numbers. In his 1883 paper,13 wherein he gives more details about his theory of irrational numbers, he says (p. 565) that it is not necessary to enter into the rational numbers because this had been done by Hermann Grassmann in his Lehrbuch der Arithmetik (1861) and J. H. T. Muller (1797-1862) in his Lehrbuch der allgemeinen Arithmetik (1855). Actually these presentations did not prove definitive. Cantor introduced a new class of numbers, the real numbers, which contain rational real and irrational real numbers. He builds the real numbers on the rationals by starting with any sequence of rationals that obeys the condition that for any given ε, all the members except a finite number differ from each other by less than ε, or that
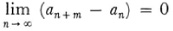
for arbitrary m. Such a sequence he calls a fundamental sequence. Each such sequence is, by definition, a real number that we can denote by b. Two such sequences (av) and (bv) are the same real number if and only if Öav. — bv approaches zero as ? becomes infinite.
For such sequences three possibilities present themselves. Given any arbitrary rational number, the members of the sequence for sufficiently large ? are all smaller in absolute value than the given number; or, from a given ? on, the members are all larger than some definite positive rational member p; or, from a given ? on, the members are all smaller than some definite negative rational number — p. In the first case b = 0; in the second b = 0; in the third b = b.
If (av) and (a’v) are two fundamental sequences, denoted by b and b’, then one can show that (av ± a’v) and (av-a’v) are fundamental sequences. These define b ± b’ and b-b’. Moreover, if b = 0, then (a’v/av) is also a fundamental sequence that defines b/b.
The rational real numbers are included in the above definition of real numbers, because, for example, any sequence (av.) with a, equal to the rational number a for each v defines the rational real number a.
Now one can define the equality and inequality of any two real numbers. Indeed b = b′, b < b′, or b < b′, according as b — V equals 0, is greater than 0 or is less than 0.
The next theorem is crucial. Cantor proves that if (bv) is any sequence of real numbers (rational or irrational), and if lim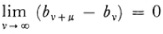 
for arbitrary μ, then there is a unique real number b, determined by a fundamental sequence (av) of rational av, such that
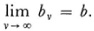
That is, the formation of fundamental sequences of real numbers does not create the need for still newer types of numbers that can serve as limits of these fundamental sequences, because the already existing real numbers suffice to provide the limits. In other words, from the standpoint of providing limits for fundamental sequences (or what amounts to the same thing, sequences which satisfy Cauchy’s criterion of convergence), the real numbers are a complete system.
Dedekind’s theory of irrational numbers, presented in his book of 1872 mentioned above, stems from ideas he had in 1858. At that time he had to give lectures on the calculus and realized that the real number system had no logical foundation. To prove that a monotonically increasing quantity that is bounded approaches a limit he, like the other authors, had to resort to geometrical evidence. (He says that this is still the way to do it in the first treatment of the calculus, especially if one does not wish to lose much time.) Moreover, many basic arithmetic theorems were not proven. He gives as an example the fact that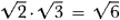 
had not yet been strictly demonstrated.
He then states that he presupposes the development of the rational numbers, which he discusses briefly. To approach the irrational numbers he asks first what is meant by geometrical continuity. Contemporary and earlier thinkers—for example, Bolzano—believed that continuity meant the existence of at least one other number between any two, the property now known as denseness. But the rational numbers in themselves form a dense set. Hence denseness is not continuity.
Dedekind obtained the suggestion for the definition of an irrational number by noting that in every division of the line into two classes of points such that every point in one class is to the left of each point in the second, there is one and only one point that produces the division. This fact makes the line continuous. For the line it is an axiom. He carried this idea over to the number system. Let us consider, Dedekind says, any division of the rational numbers into two classes such that any number in the first class is less than any number in the second. Such a division of the rational numbers he calls a cut. If the classes are denoted by Ay and A2, then the cut is denoted by (Ay, A2) From some cuts, namely, those determined by a rational number, there is either a largest number in Ay or a smallest number in A2. Conversely every cut in the rationals in which there is a largest number in the first class or a smallest in the second is determined by a rational number.
But there are cuts that are not determined by rational numbers. If we put into the first class all negative rational numbers and all positive ones whose squares are less than 2, and put into the second class all the other rationals, then this cut is not determined by a rational number. To each such cut “we create a new irrational member ? which is fully defined by this cut; we will say that the number a corresponds to this cut or that it brings about this cut.” Hence there corresponds to each cut one and only one either rational or irrational number.
Dedekind’s language in introducing irrational numbers leaves a little to be desired. He introduces the irrational a as corresponding to the cut and defined by the cut. But he is not too clear about where a comes from. He should say that the irrational number ? is no more than the cut. In fact Heinrich Weber told Dedekind this, and in a letter of 1888 Dedekind replied that the irrational number a is not the cut itself but is something distinct, which corresponds to the cut and which brings about the cut. Likewise, while the rational numbers generate cuts, they are not the same as the cuts. He says we have the mental power to create such concepts.
He then defines when one cut (A1, A2) is less than or greater than another cut (B1, B2). After having defined inequality, he points out that the real numbers possess three provable properties: (1) If α > β and β > έ, then α > γ. (2) If α and γ are two different real numbers, then there is an infinite number of different numbers which lie between α and γ. (3) If α is any real number, then the real numbers are divided into two classes A1 and A2, each of which contains an infinite number of members, and each member of Ay is less than a and each member of A2 is greater than a. The number a itself can be assigned to either class. The class of real numbers now possesses continuity, which he expresses thus: If the set of all real numbers is divided into two classes Ay and A2 such that each member of Ax is less than all members of A2, then there exists one and only one number a which brings about this division.
He defines next the operations with real numbers. Addition of the cuts (Ay, A2) and (By, B2) is defined thus: If ? is any rational number, then we put it in the class Cf if there is a number ay in Ay and a number by in By such that ay + by > c. All other rational numbers are put in the class C”2. This pair of classes Cy and C2 forms a cut (C\, C2) because every member of Cy is less than every member of C2. The cut (6"1; C2) is the sum of (Ay, A2) and (By, B2 )). The other operations, he says, arc defined analogously. He can now establish properties such as the associative and commutative properties of addition and multiplication. Though Dedekind’s theory of irrational numbers, with minor modifications such as the one indicated above, is logically satisfactory, Cantor criticized it because cuts do not appear naturally in analysis.
There are other approaches to the theory of irrational numbers beyond those already mentioned or described. For example, Wallis in 1696 had identified rational numbers and periodic decimal numbers. Otto Stolz (1842-1905), in his Vorlesungen über allgemeine Arithmetik,14 showed that every irrational number can be represented as a nonperiodic decimal and this fact can be used as a defining property.
It is apparent from these various approaches that the logical definition of the irrational number is rather sophisticated. Logically an irrational number is not just a single symbol or a pair of symbols, such as a ratio of two integers, but an infinite collection, such as Cantor’s fundamental sequence or Dedekind’s cut. The irrational number, logically defined, is an intellectual monster, and we can see why the Greeks and so many later generations of mathematicians found such numbers difficult to grasp.
Advances in mathematics arc not greeted with universal approbation. Hermann Hankel, himself the creator of a logical theory of rational numbers, objected to the theories of irrational numbers.15 “Every attempt to treat the irrational numbers formally and without the concept of [geometric] magnitude must lead to the most abstruse and troublesome artificialities, which, even if they can be carried through with complete rigor, as we have every right to doubt, do not have a higher scientific value.”
The next step in the erection of foundations for the number system was the definition and deduction of the properties of the rational numbers. As already noted, one or two efforts in this direction preceded the work on irrational numbers. Most of the workers on the rational numbers assumed that the nature and properties of the ordinary integers were known and that the problem was to establish logically the negative numbers and fractions.
The first such effort was made by Martin Ohm (1792-1872), a professor in Berlin and brother of the physicist, in his Versuch eines vollkommen conse-quenlen Systems der Mathematik (Study of a Complete Consistent System of Mathematics, 1822). Then Weierstrass, in lectures given during the 1860s, derived the rational numbers from the natural numbers by introducing the positive rationals as couples of natural numbers, the negative integers as another type of couple of natural numbers, and the negative rationals as couples of negative integers. This idea was utilized independently by Peano, and so we shall present it in more detail later in connection with his work. Weierstrass did not feel the need to clarify the logic of the integers. Actually his theory of rational numbers was not free of difficulties. However, in his lectures from 1859 on, he did affirm correctly that once the whole numbers were admitted there was no need for further axioms to build up the real numbers.
The key problem in building up the rational number system was the founding of the ordinary integers by some process and the establishment of the properties of the integers. Among those who worked on the theory of the
integers, a few believed that the whole numbers were so fundamental that no logical analysis of them could be made. This position was taken by Kronecker, who was motivated by philosophical considerations into which we shall enter more deeply later. Kronecker too wished to arithmetize analysis, that is, to found analysis on the integers; but he thought one could not go beyond recognition of knowledge of the integers. Of these man has a fundamental intuition. “God made the integers,” he said, “all else is the work of man.”
Dedekind gave a theory of the integers in his Was sind und was sollen die Zahlen.16 Though published in 1888, the work dates from 1872 to 1878. He used set-theoretic ideas, which by this time Cantor had already advanced, and which were to assume great importance. Nevertheless, Dedekind’s approach was so complicated that it was not accorded much attention.
The approach to the integers that best suited the axiomatizing proclivities of the late nineteenth century was to introduce them entirely by a set of axioms. Giuseppe Peano (1858-1932) also accomplished this in his Arithmetices Principia Nova Methodo Exposita (1889).17 Presumably he was influenced by Dedekind’s 1888 work but he gave his own slant to the ideas. Since Peano’s approach is very widely used we shall review it.
Peano used a great deal of symbolism because he wished to sharpen the reasoning. Thus ε means to belong to; means implies; N0 means the class of natural numbers; and a+ denotes the next natural number after a. Peano used this symbolism in his presentation of all of mathematics, notably in his Formulario malhemalico (5 vols., 1895-1908). He used it also in his lectures, and the students rebelled. He tried to satisfy them by passing all of them, but that did not work, and he was obliged to resign his professorship at a military academy and he remained at the University of Turin.
Though Peano’s work influenced the further development of symbolic logic and the later movement of Frege and Russell to build mathematics on logic, his work must be distinguished from that of Frege and Russell. Peano did not wish to build mathematics on logic. To him, logic was the servant of mathematics.
Peano started with the undefined concepts (cf. Chap. 42, sec. 2) of “set,” “natural numbers,” “successor,” and “belong to.” His five axioms for the natural numbers are:
(1) 1 is a natural number.
(2) 1 is not the successor of any other natural number.
(3) Each natural number a has a successor.
(4) If the successors of a and b are equal then so are a and b.
(5) If a set S of natural numbers contains 1 and if when S contains any number a it also contains the successor of a, then S contains all the natural numbers.
This last axiom is the axiom of mathematical induction.
Peano also adopted the reflexive, symmetric, and transitive axioms for equality. That is, a = a; if a — b, then b = a; and if a = b and b = c, then a = c. He defined addition by the statements that for each pair of natural numbers a and b there is a unique sum such that
a + 1 = a +
a + (b +) = (a + b)+.
Likewise, multiplication was defined by the statement that to each pair of natural numbers a and b there is a unique product such that
a· 1 = a
a·b+ = (a·b) + a.
He then established all the familiar properties of natural numbers.
From the natural numbers and their properties others found it simple to define and establish the properties of the negative whole numbers and the rational numbers. One can first define the positive and negative integers as a new class of numbers, each an ordered pair of natural numbers. Thus (a, b) where a and b are natural numbers is an integer. The intuitive meaning of (a, b) is a — b. Hence when a > b, the couple represents the usual positive integer, and when a < b, the couple represents the usual negative integer. Suitable definitions of the operations of addition and multiplication lead to the usual properties of the positive and negative integers.
Given the integers, one introduces the rational numbers as ordered couples of integers. Thus if A and x are integers, the ordered couple (A, B) is a rational number. Intuitively (A, B) is A\B. Again suitable definitions of the operations of addition and multiplication of the couples lead to the usual properties of the rational numbers.
Thus, once the logical approach to the natural numbers was attained, the problem of building up the foundations of the real number system was completed. As we have already noted, generally the men who worked on the theory of irrationals assumed that the rational numbers were so thoroughly understood that they could be taken for granted, or made only a minor gesture toward clarifying them. After Hamilton had grounded the complex numbers on the real numbers, and after the irrationals were defined in terms of the rational numbers, the logic of this last class was finally created. The historical order was essentially the reverse of the logical order required to build up the complex number system.
The essence of the approaches to the logical foundations of the real number system thus far described is to obtain the integers and their properties in some manner and, with these in hand, then to derive the negative numbers, the fractions, and finally the irrational numbers. The logical base of this approach is some series of assertions concerning the natural numbers only, for example, Peano’s axioms. All the other numbers are constructed. Hilbert called the above approach the genetic method (he may not have known Peano’s axioms at this time but he knew other approaches to the natural numbers). He grants that the genetic method may have pedagogical or heuristic value but, he says, it is logically more secure to apply the axiomatic method to the entire real number system. Before we state his reasons, let us look at his axioms.18
He introduces the undefined term, number, denoted by a, b, c,…, and then gives the following axioms:
I. Axioms of Connection
It. From the number a and the number b there arises through addition a definite number c; in symbols
a + b = c or c = a + b.
I1If a and b are given numbers, then there exists one and only one number x and also one and only one number ? so that
a + x = b and y + a = b.
I3. There is a definite number, denoted by 0, so that for each a
a + 0 = a and 0 + a = a.
I4 From the number a and the number b there arises by another method, by multiplication, a definite number c; in symbols
ab = c or c = ab.
I5 If a and b are arbitrary given numbers and a not 0, then there exists one and only one number x, and also one and only one number y such that
ax = b and ya = b.
I6 There exists a definite number, denoted by 1, such that for each a we have
a · 1 = a and 1 · a = a.
111. a + (b + c) = (a + b) + c
II2a + b = b + a.
II3a(bc) = (ab)c.
II4a(b + c) = ab + ac.
II5 (a + ¿>)c = αδ+ èc.
II6 ab = èa.
III. Axioms of Order
III1. If a and b are any two different numbers, then one of these is always greater than the other; the latter is said to be smaller; in symbols
a > b and b < a.
III2. If a > b and b > c then a > c.
III3. If a > b then it is always true that
a + c > b + c and c + a > c + b.
III4 If a > b and c > 0 then ac > be and ca > cb.
IV. Axioms of Continuity
IV1(Axiom of Archimedes) If a > 0 and è > 0 are two arbitrary numbers then it is always possible to add a to itself a sufficient number of times so that
a + a +…+ a > b.
IV2 (Axiom of Completeness) It is not possible to adjoin to the system of numbers any collection of things so that in the combined collection the preceding axioms are satisfied; that is, briefly put, the numbers form a system of objects which cannot be enlarged with the preceding axioms continuing to hold.
Hilbert points out that these axioms are not independent; some can be deduced from the others. He then affirms that the objections against the existence of infinite sets (sec. 6) are not valid for the above conception of the real numbers. For, he says, we do not have to think about the collection of all possible laws in accordance with which the elements of a fundamental sequence (Cantor’s sequences of rational numbers) can be formed. We have but to consider a closed system of axioms and conclusions that can be deduced from them by a finite number of logical steps. He does point out that it is necessary to prove the consistency of this set of axioms, but when this is done the objects defined by it, the real numbers, exist in the mathematical sense. Hilbert was not aware at this time of the difficulty of proving the consistency of axioms for real numbers.
To Hilbert’s claim that his axiomatic method is superior to the genetic method, Bertrand Russell replied that the former has the advantage of theft over honest toil. It assumes at once what can be built up from a much smaller set of axioms by deductive arguments.
As in the case of almost every significant advance in mathematics, the creation of the theory of real numbers met with opposition. Du Bois-Rey-mond, whom we have already cited as opposing the arithmetization of analysis, said in his Théorie générale des fonctions of 1887, 19
No doubt with help from so-called axioms, from conventions, from philosophic propositions contributed ad hoc, from unintelligible extensions of originally clear concepts, a system of arithmetic can be constructed which resembles in every way the one obtained from the concept of magnitude, in order thus to isolate the computational mathematics, as it were, by a cordon of dogmas and defensive definitions…. But in this way one can also invent other arithmetic systems. Ordinary arithmetic is just the one which corresponds to the concept of linear magnitude.
Despite attacks such as this, the completion of the work on the real numbers seemed to mathematicians to resolve all the logical problems the subject had faced. Arithmetic, algebra, and analysis were by far the most extensive part of mathematics and this part was now securely grounded.
The rigorization of analysis had revealed the need to understand the structure of sets of real numbers. To treat this problem Cantor had already introduced (Chap. 40, sec. 6) some notions about infinite sets of points, especially the sets of the first species. Cantor decided that the study of infinite sets was so important that he undertook to study infinite sets as such. This study, he expected, would enable him to distinguish clearly the different infinite sets of discontinuities.
The central difficulty in the theory of sets is the very concept of an infinite set. Such sets had naturally come to the attention of mathematicians and philosophers from Greek times onward, and their very nature and seemingly contradictory properties had thwarted any progress in understanding them. Zeno’s paradoxes are perhaps the first indication of the difficulties. Neither the infinite divisibility of the straight line nor the line as an infinite set of discrete points seemed to permit rational conclusions about motion. Aristotle considered infinite sets, such as the set of whole numbers, and denied the existence of an infinite set of objects as a fixed entity. For him, sets could be only potentially infinite (Chap. 3, sec. 10).
Proclus, the commentator on Euclid, noted that since a diameter of a circle divides it into halves and since there is an infinite number of diameters, there must be twice that number of halves. This seems to be a contradiction to many, Proclus says, but he resolves it by saying that one cannot speak of an actual infinity of diameters or parts of a circle. One can speak only of a larger and larger number of diameters or parts of a circle. In other words, Proclus accepted Aristotle’s concept of a potential infinity but not an actual infinity. This avoids the problem of a double infinity equaling an infinity.
Throughout the Middle Ages philosophers took one side or the other on the question of whether there can be an actual infinite collection of objects. It was noted that the points of two concentric circles could be put into one-to-one correspondence with each other by associating points on a common radius. Yet one circumference was longer than the other.
Galileo struggled with infinite sets and rejected them because they were not amenable to reason. In his Two New Sciences (pp. 18-40 of the English translation), he notes that the points of two unequal lengths AB and CD (Fig. 41.1) can be put into one-to-one correspondence with each other and so presumably contain the same number of points. He also notes that the whole numbers can be put into one-to-one correspondence with their squares merely by assigning each number to its square. But this leads to different “amounts” of infinities, which Galileo says cannot be. All infinite quantities are the same and cannot be compared.
Gauss, in his letter to Schumacher of July 12, 1831,20 says, “I protest against the use of an infinite quantity as an actual entity; this is never allowed in mathematics. The infinite is only a manner of speaking, in which one properly speaks of limits to which certain ratios can come as near as desired, while others are permitted to increase without bound.” Cauchy, like others before him, denied the existence of infinite sets because the fact that a part can be put into one-to-one correspondence with the whole seemed contradictory to him.
The polemics on the various problems involving sets were endless and
involved metaphysical and even theological arguments. The attitude of most mathematicians toward this problem was to ignore what they could not solve. On the whole they also avoided the explicit recognition of actually infinite sets, though they used infinite series, for example, and the real number system. They would speak of points of a line and yet avoid saying that the line is composed of an infinite number of points. This avoidance of troublesome problems was hypocritical, but it did suffice to build classical analysis. However, when the nineteenth century faced the problem of instituting rigor in analysis, it could no longer side-step many questions about infinite sets.
Bolzano, in his Paradoxes of the Infinite (1851), which was published three years after his death, was the first to take positive steps toward a definitive theory of sets. He defended the existence of actually infinite sets and stressed the notion of equivalence of two sets, by which he meant what was later called the one-to-one correspondence between the elements of the two sets. This notion of equivalence applied to infinite sets as well as finite sets. He noted that in the case of infinite sets a part or subset could be equivalent to the whole and insisted that this must be accepted. Thus the real numbers between 0 and 5 can be put into one-to-one correspondence with the real numbers between 0 and 12 through the formula y = 12x/5, despite the fact that the second set of numbers contains the first set. Numbers could be assigned to infinite sets and there would be different transfinite numbers for different infinite sets, though Bolzano’s assignment of transfinite numbers was incorrect according to the later theory of Cantor.
Bolzano’s work on the infinite was more philosophical than mathematical and did not make sufficiently clear the notion of what was called later the power of a set or the cardinal number of a set. He, too, encountered properties that appeared paradoxical to him, and these he cites in his book. He decided that transfinite numbers were not needed to found the calculus and so did not pursue them farther.
The creator of the theory of sets is Georg Cantor (1845-1918) who was born in Russia of Danish-Jewish parentage but moved to Germany with his parents. His father urged him to study engineering and Cantor entered the University of Berlin in 1863 with that intention. There he came under the influence of Weierstrass and turned to pure mathematics. He became Privatdozent at Halle in 1869 and professor in 1879. When he was twenty-nine he published his first revolutionary paper on the theory of infinite sets in the Journal für Mathematik. Although some of its propositions were deemed faulty by the older mathematicians, its overall originality and brilliance attracted attention. He continued to publish papers on the theory of sets and on transfinite numbers until 1897.
Cantor’s work which resolved age-old problems and reversed much previous thought, could hardly be expected to receive immediate acceptance. His ideas on transfinite ordinal and cardinal numbers aroused the hostility of the powerful Leopold Kronecker, who attacked Cantor’s ideas savagely over more than a decade. At one time Cantor suffered a nervous breakdown, but resumed work in 1887. Even though Kronecker died in 1891, his attacks left mathematicians suspicious of Cantor’s work.
Cantor’s theory of sets is spread over many papers and so we shall not attempt to indicate the specific papers in which each of his notions and theorems appear. These papers are in the Mathematische Annalen and the Journal für Mathematik from 1874 on.21 By a set Cantor meant a collection of definite and separate objects which can be entertained by the mind and to which we can decide whether or not a given object belongs. He says that those who argue for only potentially infinite sets are wrong, and he refutes the earlier arguments of mathematicians and philosophers against actually infinite sets. For Cantor a set is infinite if it can be put into one-to-one correspondence with part of itself. Some of his set-theoretic notions, such as limit point of a set, derived set, and set of the first species, were defined and used in a paper on trigonometric series;22 these we have already described in the preceding chapter (sec. 6). A set is closed if it contains all its limit points. It is open if every point is an interior point, that is, if each point may be enclosed in an interval that contains only points of the set. A set is perfect if each point is a limit point and the set is closed. He also defined the union and intersection of sets. Though Cantor was primarily concerned with sets of points on a line or sets of real numbers, he did extend these notions of set theory to sets of points in ?-dimensional Euclidean space.
He sought next to distinguish infinite sets as to “size” and, like Bolzano, decided that one-to-one correspondence should be the basic principle. Two sets that can be put into one-to-one correspondence are equivalent or have the same power. (Later the term “power” became “cardinal number.”) Two sets may be unequal in power. If of two sets of objects M and ?, N can be put into one-to-one correspondence with a subset of Al but M cannot be put into one-to-one correspondence with a subset of N, the power of M is larger than that of N.
Sets of numbers were of course the most important, and so Cantor illustrates his notion of equivalence or power with such sets. He introduces the term “enumerable” for any set that can be put into one-to-one correspondence with the positive integers. This is the smallest infinite set. Then
Cantor proved that the set of rational numbers is enumerable. He gave one proof in 1874.23 However, his second proof24 is the one now most widely used and we shall describe it.
The rational numbers are arranged thus:
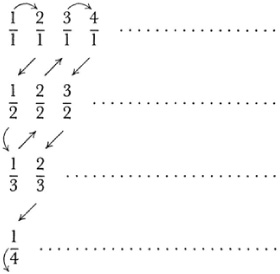
It will be noted that all those in any one diagonal have the same sum of numerator and denominator. Now one starts with 1/1 and follows the arrows assigning the number 1 to 1/1, 2 to 2/1, 3 to 1/2, 4 to 1/3, and so on. Every rational number will be reached at some stage and to each one a finite integer will be assigned. Hence the above set of rational numbers (in which some appear many times) is in one-to-one correspondence with the integers. Then if duplicates are eliminated the set of rational numbers will still be infinite and necessarily enumerable since this is the smallest infinite set.
Still more surprising is Cantor’s proof in the 1874 paper just referred to that the set of all algebraic numbers, that is, the set of all numbers that are solutions of all algebraic equations
a0xn + a1xn-1 +… + an = 0,
where the a¡ are integers, is also enumerable.
To prove this, he assigns to any algebraic equation of degree ? the height ?? defined by
N = n — 1 + |a0| + |a1| +… + |an|
where the a¡ are the coefficients of the equation. The height ?? is an integer. To each N there corresponds only a finite number of algebraic equations and hence only a finite number of algebraic numbers, say Φ(N). Thus Φ(1) = 1; Φ(2) = 2; Φ(3) = 4. He starts with N = 1 and labels the corresponding algebraic numbers from 1 to αδ; the algebraic numbers that have
height 2 are labeled from n1 + 1 to n2; and so forth. Because each algebraic number will be reached and be assigned to one and only one integer, the set of algebraic numbers is enumerable.
In his correspondence with Dedekind in 1873, Cantor posed the question of whether the set of real numbers can be put into one-to-one correspondence with the integers, and some weeks later he answered in the negative. He gave two proofs. The first (in the 1874 article just referred to) is more complicated than the second,25 which is the one most often used today. It also has the advantage, as Cantor pointed out, of being independent of technical considerations about irrational numbers.
Cantor’s second proof that the real numbers are uncountable (non-enumerable) begins by assuming that the real numbers between 0 and 1 are countable (enumerable). Let us write each as a decimal and let us agree that a number such as 1/2 will be written as.4999…. If these real numbers are countable, then we can assign each one to an integer n, thus:
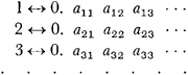
Now let us define a real number between 0 and 1 thus: Let b = 0. b1 b b2 b b3. …, where bk = 9 if akk = 1 and bk = 1 if a kk 1. This real number differs from any of those in the above correspondence. However, this was supposed to contain all the real numbers between 0 and 1. Hence there is a contradiction.
Since the real numbers are uncountable and the algebraic numbers are countable, there must be transcendental irrationals. This is Cantor’s nonconstructive existence proof, which should be compared with Liouville’s actual construction of transcendental irrationals (sec. 2).
In 1874 Cantor occupied himself with the equivalence of the points of a line and the points of Rn (?-dimcnsional space) and sought to prove that a one-to-one correspondence between these two sets was impossible. Three years later he proved that there is such a correspondence. He wrote to Dedekind,26 “I see it but I do not believe it.”
The idea27 used to set up this one-to-one correspondence can be exhibited readily if we set up such a correspondence between the points of the unit square and the points of the segment (0, 1). Let (x, y) be a point of the unit square and ? a point of the unit interval. Let ? and y be represented by infinite decimals so that in a finite decimal terminating in zero, we replace the 0 by an infinite sequence of 9’s. We now break up ? and y
into groups of decimals, each group ending with the first nonzero digit encountered. Thus
x =.3 002 03 04 6 · · ·
y =.01 6 07 8 09 · · ·
Form
z =.3 01 002 6 03 07 04 8 6 09…
by choosing as the groups in ? the first group from x, then the first from y, and so forth. If two x’s or ?/’s differ in some digit then the corresponding z’s will differ. Hence to each (x, y) there is a unique z. Given a z, one breaks up its decimal representation into the groups just described and forms the ? and y by reversing the above process. Again two different z’s will yield two different pairs (x, y) so that to each ? there is a unique (x, y). The one-to-one correspondence just described is not continuous; roughly stated, this means that neighboring z-points do not necessarily go into neighboring (x, #)-points, nor conversely.
Du Bois-Reymond objected to this proof.28 “It appears repugnant to common sense. The fact is that this is simply the conclusion of a type of reasoning which allows the intervention of idealistic fictions, wherein one lets them play the role of genuine quantities even though they are not even limits of representations of quantities. This is where the paradox resides.”
Having demonstrated the existence of sets with the same power and different powers, Cantor pursued this concept of the power of a set and introduced a theory of cardinal and ordinal numbers in which the transfinite cardinals and ordinals are the striking elements. Cantor developed this work in a series of papers in the Mathematische Annalen from 1879 to 1884, all under the title “Über unendliche lineare Punktmannichfaltigkeiten” (On Infinite Linear Aggregates of Points). Then he wrote two definitive papers in 1895 and 1897 in the same journal.29
In the fifth paper on linear aggregates30 Cantor opens with the observation,
The description of my investigations in the theory of aggregates has reached a stage where their continuation has become dependent on a generalization of real positive integers beyond the present limits; a generalization which takes a direction in which, as far as I know, nobody has yet looked.
I depend on this generalization of the number concept to such an extent that without it I could not freely take even small steps forward in the theory of sets. I hope that this situation justifies or, if necessary, excuses the introduction of seemingly strange ideas into my arguments. In fact the purpose is to generalize or extend the series of real integers beyond infinity. Daring as this might appear, I express not only the hope but also the firm conviction that in due course this generalization will be acknowledged as a quite simple, appropriate, and natural step. Still I am well aware that by adopting such a procedure I am putting myself in opposition to widespread views regarding infinity in mathematics and to current opinions on the nature of number.
He points out that his theory of infinite or transfinite numbers is distinct from the concept of infinity wherein one speaks of a variable becoming infinitely small or infinitely large. Two sets which are in one-to-one correspondence have the same power or cardinal number. For finite sets the cardinal number is the usual number of objects in the set. For infinite sets new cardinal numbers are introduced. The cardinal number of the set of whole numbers he denoted by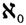 
o. Since the real numbers cannot be put into one-to-one correspondence with the whole numbers, the set of real numbers must have another cardinal number which is denoted by c, the first letter of continuum. Just as in the case of the concept of power, if two sets M and jVare such that jVcan be put into one-to-one correspondence with a subset of M but M cannot be put into one-to-one correspondence with a subset of N, the cardinal number of AI is greater than that of N. Then c >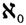
To obtain a cardinal number larger than a given one,31 one considers any set M which the second cardinal number represents and considers the set N of all the subsets of AI. Among the subsets of AI are the individual elements of AI, all pairs of elements of Aí, and so on. Now it is certainly possible to set up a one-to-one correspondence between M and a subset of N because one subset of N consists of all the individual members of N (each regarded as a set and as a member of N), and these members are the very members of AI. It is not possible to set up a one-to-one correspondence between AI and all the members of N. For suppose such a one-to-one correspondence were set up. Let m be any member of M and let us consider all the m’s such that the subsets (members) of N that are associated with m’s of Al do not contain the m to which they correspond under this supposed one-to-one correspondence. Let ? be the set of all these m’s. ? is of course a member of ?7. Cantor affirms that ? is not included in the supposed one-to-one correspondence. For if ? corresponded to some m of Aí, and ? contained m,
that would be a contradiction of the very definition of η. On the other hand if η did not contain m, it should because η was by definition the set of all m’s which were not contained in the corresponding subsets of N. Hence the assumption that there is a one-to-one correspondence between the elements m of M and of N, which consists of all the subsets of M, leads to a contradiction. Then the cardinal number of the set consisting of all the subsets of a given set is larger than that of the given set.
Cantor defined the sum of two cardinal numbers as the cardinal number of the set that is the union of the (disjoined) sets represented by the summands. Cantor also defined the product of any two cardinal numbers. Given two cardinal numbers α and α, one takes a set M represented by α and a set N represented by α and forms the pairs of elements (m, n) where m is any element of M and M of N. Then the cardinal number of the set of all possible pairs is the product of α and β.
Powers of cardinal numbers are also defined. If we have a set M of m objects and a set N of n objects, Cantor defines the set mn, and this amounts to the set of permutations of m objects n at a time with repetitions of the m objects permitted. Thus if m — 3 and n = 2 and we have m1, m2, m3, the permutations are
m1m1 m2m2 m3m1
m1m2 m2m1 m3m2
m1m3 m2m3 m3m3
Cantor calls attention to the fact that his theory of cardinal numbers applies in particular to finite cardinals, and so he has given “ the most natural, shortest, and most rigorous foundation for the theory of finite numbers.”
The next concept is that of ordinal number. He has already found the need for this concept in his introduction of successive derived sets of a given point set. He now introduces it abstractly. A set is simply ordered if any two elements have a definite order so that given m 1 and m2 either m1 precedes m2 or m2 precedes m1; the notation is m1 < m 2 or m2. Further if in1 < m 2 and m2 < m 3, then simple order also implies xc < m 3; that is, the order relationship is transitive. An ordinal number of an ordered set M is the order type of the order in the set. Two ordered sets are similar if there is a one-to-one correspondence between them and if, when mi corresponds to ZÍJ and m2 to n2 and m1 < m 2, then ?? < n 2. Two similar sets have the same type or ordinal number. As examples of ordered sets, we may use any finite set of numbers in any given order. For a finite set, no matter what the order is, the ordinal number is the same and the symbol for it can be taken to be the cardinal number of the set of numbers in the set. The ordinal number of the set of positive integers in their natural order is denoted by ?. On the other hand, the set of positive integers in decreasing order, that is
…,4, 3, 2, 1
is denoted by *ω. The set of positive and negative integers and zero in the usual order has the ordinal number *ω + ω.
Then Cantor defines the addition and multiplication of ordinal numbers. The sum of two ordinal numbers is the ordinal number of the first ordered set plus the ordinal number of the second ordered set taken in that specific order. Thus the set of positive integers followed by the first five integers, that is,
12 3·· 1 2 3 4 5
has the ordinal number ω + 5. Also the equality and inequality of ordinal numbers is defined in a rather obvious way.
And now he introduces the full set of transfinite ordinals, partly for their own value and partly to define precisely higher transfinite cardinal numbers. To introduce these new ordinals he restricts the simply ordered sets to well-ordered sets.32 A set is well-ordered if it has a first element in the ordering and if every subset has a first element. There is a hierarchy of ordinal numbers and cardinal numbers. In the first class, denoted by Z 1;are the finite ordinals
1,2, 3,···.
In the second class, denoted by Z2, are the ordinals
ω, ω + 1, ω + 2,…, 2ω, 2ω + 1,…,3ω,3ω + 1,…, ω2,ω3,…, ωω,…
Each of these ordinals is the ordinal of a set whose cardinal number is .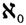
The set of ordinals in Z2 has a cardinal number is 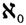. The set is not enumerable and so Cantor introduces a new cardinal number 
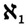as the cardinal number of the set Z2. is then shown to be the next cardinal after .
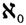The ordinals of the third class, denoted by Z3, are
Ω, Ω + 1, Ω + 2,…, Ω + Ω,…
These are the ordinal numbers of well-ordered sets, each of which has 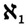elements. However, the set of ordinals Z3 has more than 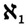elements, and Cantor denotes the cardinal number of the set Z3 by. This hierarchy of ordinals and cardinals can be continued indefinitely.
Now Cantor had shown that given any set, it is always possible to create a new set, the set of subsets of the given set, whose cardinal number is larger than that of the given set. If 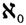is the given set, then the cardinal number of the set of subsets is 2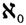. Cantor had proved that 2 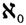= c, where c is the cardinal number of the continuum. On the other hand he introduced 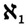xthrough the ordinal numbers and proved that 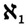is the next cardinal after 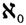. Hence 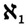≤ c, but the question as to whether Xx = c, known as the continuum hypothesis, Cantor, despite arduous efforts, could not answer. In a list of outstanding problems presented at the International Congress of Mathematicians in 1900, Hilbert included this (Chap. 43, sec. 5; see also Chap. 51, sec. 8).
For general sets M and Nit is possible that M cannot be put into one-to-one correspondence with any subset of N and N cannot be put into one-to-one correspondence with a subset of M. In this case, though M and N have cardinal numbers α and β, say, it is not possible to say that β = α, β < β, or α > β. That is, the two cardinal numbers are not comparable. For well-ordered sets Cantor was able to prove that this situation cannot arise. It seemed paradoxical that there should be non-well-ordered sets whose cardinal numbers cannot be compared. But this problem, too, Cantor could not solve.
Ernst Zermelo (1871-1953) took up the problem of what to do about the comparison of the cardinal numbers of sets that are not well-ordered. In 190433 he proved, and in 190834 gave a second proof, that every set can be well-ordered (in some rearrangement). To make the proof he had to use what is now known as the axiom of choice (Zermelo’s axiom), which states that given any collection of nonempty, disjoined sets, it is possible to choose just one member from each set and so make up a new set. The axiom of choice, the well-ordering theorem, and the fact that any two sets may be compared as to size (that is, if their cardinal numbers are α and β, either α = β, α > β, or ? > ?) are equivalent principles.
Cantor’s theory of sets was a bold step in a domain that, as already noted, had been considered intermittently since Greek times. It demanded strict application of purely rational arguments, and it affirmed the existence of infinite sets of higher and higher power, which are entirely beyond the grasp of human intuition. It would be singular if these ideas, far more revolutionary than most others previously introduced, had not met with opposition. The doubts as to the soundness of this development were rein-
forced by questions raised by Cantor himself and by others. In letters to Dedekind of July 28 and August 28, 1899,35 Cantor asked whether the set of all cardinal numbers is itself a set, because if it is it would have a cardinal number larger than any other cardinal. He thought he answered this in the negative by distinguishing between consistent and inconsistent sets. However, in 1897 Cesare Burali-Forti (1861-1931) pointed out that the sequence of all ordinal numbers, which is well-ordered, should have the greatest of all ordinal numbers as its ordinal number.36 Then this ordinal number is greater than all the ordinal numbers. (Cantor had already noted this difficulty in 1895.) These and other unresolved problems, called paradoxes, were beginning to be noted by the end of the nineteenth century.
The opposition did make itself heard. Kronecker, as we have already observed, opposed Cantor’s ideas almost from the start. Felix Klein was by no means in sympathy with them. Poincaré37 remarked critically, “But it has happened that we have encountered certain paradoxes, certain apparent contradictions which would have pleased Zeno of Elea and the school of Megara. … I think for my part, and I am not the only one, that the important point is never to introduce objects that one cannot define completely in a finite number of words.” He refers to set theory as an interesting “pathological case.” He also predicted (in the same article) that “Later generations will regard [Cantor’s] Mengenlehre as a disease from which one has recovered.” Hermann Weyl spoke of Cantor’s hierarchy of alephs as a fog on a fog.
However, many prominent mathematicians were impressed by the uses to which the new theory had already been put. At the first International Congress of Alathematicians in Zurich (1897), Adolf Hurwitz and Hadamard indicated important applications of the theory of transfinite numbers to analysis. Additional applications were soon made in the theory of measure (Chap. 44) and topology (Chap. 50). Hilbert spread Cantor’s ideas in Germany, and in 192638 said, “No one shall expel us from the paradise which Cantor created for us.” He praised Cantor’s transfinite arithmetic as “the most astonishing product of mathematical thought, one of the most beautiful realizations of human activity in the domain of the purely intelligible.”39 Bertrand Russell described Cantor’s work as “probably the greatest of which the age can boast.”
Becker, Oskar: Grundlagen der Mathematik in geschichtlicher Entwicklung, Verlag Karl Alber, 1954, pp. 217-316.
Boyer, Carl ?.: A History of Mathematics, John Wiley and Sons, 1968, Chap. 25.
Cantor, Georg: Gesammelte Abhandlungen, 1932, Georg Olms (reprint), 1962.
–––: Contributions to the Founding of the Theory of Transfinite Numbers, Dover (reprint), no date. This contains an English translation of Cantor’s two key papers of 1895 and 1897 and a very helpful introduction by P. E. B. Jourdain.
Cavaillès, Jean: Philosophie mathématique, Hermann, 1962. Also contains the Cantor-Dedekind correspondence translated into French.
Dedekind, R.: Essays on the Theory of Numbers, Dover (reprint), 1963. Contains an English translation of Dedekind’s “Stetigkeit und irrationale Zahlen” and “Was sind und was sollen die Zahlen.” Both essays are in Dedekind’s Werke, 3, 314-34 and 335-91.
Fraenkel, Abraham ?.: “Georg Cantor,” Jahres, der Deut. Math.-Verein., 39, 1930, 189-266. A historical account of Cantor’s work.
Helmholtz, Hermann von: Counting and Measuring, D. Van Nostrand, 1930. English translation of Hclmholtz’s Zählen und Alessen, Wissenschaftliche Abhandlungen, 3, 356-91.
Manheim, Jerome ?.: The Genesis of Point Set Topology, Macmillan, 1964, pp. 76-1 10.
Meschkowski, Herbert: Ways of Thought of Great Mathematicians, Holden-Day, 1964, pp. 91-104.
———: Evolution of Mathematical Thought, Holden-Day, 1965, Chaps. 4-5.
———: Probleme des Unendlichen: Werk und Leben Georg Cantors, F. Vieweg und Sohn, 1967.
Noether, E. andj. Cavaillès: Briefwechsel Cantor-Dedekind, Hermann, 1937.
Peano G.: Opere scelte, 3 vols., Edizioni Cremonese, 1957-59.
Schoenflies, Arthur M.: Die Entwicklung der Mengenlehre und ihre Anwendungen, two parts, B. G. Teubner, 1908, 1913.
Smith, David Eugene: A Source Book in Mathematics, Dover (reprint), 1959, Vol. 1, pp. 35-45, 99-106.
Stammler, Gerhard: Der Zahlbegriff seit Gauss, Georg Olms, 1965.