Chapter 5

Grouping Your Way into Accurate Predictions

IN THIS CHAPTER

Understanding the basics of clustering, classification, and other grouping algorithms

Clustering your data with the k-means algorithm and kernel density estimation

Choosing between decision trees and random forests

Getting to know hierarchical and neighborhood clustering algorithms

Working through nearest neighbor algorithms

When it comes to making predictions from data, grouping techniques can be a simple and powerful way to generate valuable insights quickly. Although grouping methods tend to be relatively simple, you can choose from quite a few approaches. In this chapter, I introduce you to classification, and clustering algorithms, as well as decision trees and random forests.

Data scientists use clustering to help them divide their unlabeled data into subsets. If they’re starting with labeled data, they can use classification methods to build predictive models that they can then use to forecast the classification of future observations. Classification is a form of supervised machine learning — the classification algorithm essentially learns from your labeled data.

Though the basics behind clustering and classification seem relatively easy to understand at first, things get tricky fast when you get into using some of the more advanced algorithms. I start you out with the simplest approach — clustering — and then lightly touch on decision trees and random forests before I help you, lastly, tackle instance-based learning classification algorithms.

Starting with Clustering Basics

To grasp advanced methods for use in clustering your data, first take a few moments to grasp the basics that underlie all forms of clustering. Clustering is a form of machine learning — the machine in this case is your computer, and learning refers to an algorithm that’s repeated over and over until a certain set of predetermined conditions is met. Learning algorithms are generally run until the point that the final analysis results won’t change, no matter how many additional times the algorithm is passed over the data.

Clustering is one of the two main types of machine learning: unsupervised machine learning. In unsupervised machine learning, the data in the dataset is unlabeled. Because the data is unlabeled, the algorithms must use inferential methods to discover patterns, relationships, and correlations within the raw dataset. To put clustering through its paces, I want to use a readily available sample dataset from the World Bank’s open datasets on country income and education. This data shows the percentage of income earned by the bottom 10 percent of the population in each country and the percentage of children who complete primary school in each country.

For this chapter’s discussion, I’m isolating the median reported statistic from the years 2000 to 2003. (Some countries report on these statistics only every few years, and during 2000 to 2003, this data was fully reported by 81 of 227 countries.)

In datasets about the percentage of children who complete primary school, some are reported at more than 100 percent. That’s because some countries count this statistic at different ages, but the data was normalized so that the percentage distribution is proportionally scaled across the range of countries represented in the dataset. In other words, although the total scale exceeds 100 percent, the values have been normalized so that they’re proportional to one another and you’re getting an apples-to-apples comparison. Thus, the fact that some countries report completion rates greater than 100 percent has no adverse effect on the analysis you make in this chapter.

Getting to know clustering algorithms

You use clustering algorithms to subdivide unlabeled datasets into clusters of observations that are most similar for a predefined feature. If you have a dataset that describes multiple features about a set of observations and you want to group your observations by their feature similarities, use clustering algorithms.

Over on the companion website to this book (http://www.businessgrowth.ai/), you’ll find a free training-and-coding demonstration of how to use clustering in Python for a popular use case — customer profiling and segmentation.

You can choose from various clustering methods, depending on how you want your dataset to be divided. The two main types of clustering algorithms are

• Partitional: Algorithms that create only a single set of clusters
• Hierarchical: Algorithms that create separate sets of nested clusters, each in its own hierarchical level

You can read about both approaches later in this chapter, but for now, start by looking at Figure 5-1, a simple scatterplot of the Country Income and Education datasets.

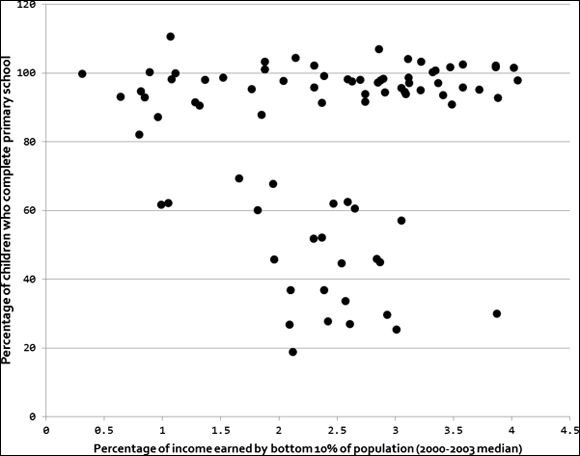
FIGURE 5-1: A simple scatterplot.

In unsupervised clustering, you start with this data and then proceed to divide it into subsets. These subsets, called clusters, are composed of observations that are most similar to one another. In Figure 5-1, it appears that the scatterplot has at least two clusters, and probably three — one at the bottom with low income and education, and then the high-education countries look like they might be split between low and high incomes.

Figure 5-2 shows the result of eyeballing, or making a visual estimate of, clusters in this dataset.

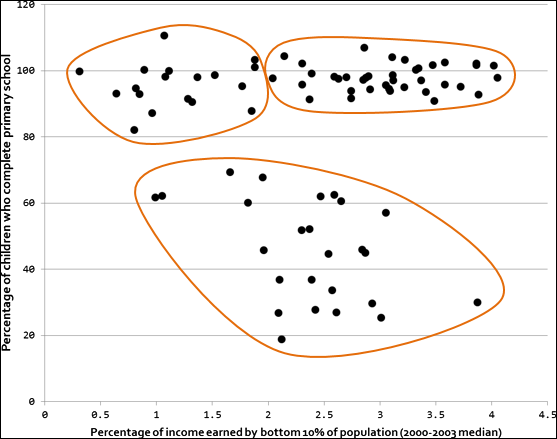
FIGURE 5-2: A simple scatterplot, showing eyeballed estimations of clustering.

Although you can generate visual estimates of clusters, you can achieve much more accurate results when dealing with much larger datasets by using algorithms to generate clusters for you. Visual estimation is a rough method that’s useful only on smaller datasets of minimal complexity. Algorithms produce exact, repeatable results, and you can use algorithms to generate clusters from multiple dimensions of data within your dataset.

Clustering algorithms are appropriate in situations where the following characteristics are true:

• You know and understand the dataset you’re analyzing.
• Before running the clustering algorithm, you don’t have an exact idea of the nature of the subsets (clusters). Often, you don’t even know how many subsets are in the dataset before you run the algorithm.
• The subsets (clusters) are determined by only the single dataset you’re analyzing.
• Your goal is to determine a model that describes the subsets in a single dataset and only this dataset.

If you add more data to your dataset after you’ve already built the model, be sure to rebuild the model from scratch to produce more complete and accurate model results.

Examining clustering similarity metrics

Clustering is based on calculating the similarity or difference between two observations. If your dataset is numeric — composed of only numerical features — and can be portrayed on an n-dimensional plot, you can use various geometric metrics to scale your multidimensional data.

An n-dimensional plot is a multidimensional scatterplot that you can use to plot n number of dimensions of data.

Some popular geometric metrics, used for calculating distances between observations include:

• Euclidean: A measure of the distance between points plotted on a Euclidean plane.
• Manhattan: A measure of the distance between points where distance is calculated as the sum of the absolute value of the differences between two points’ Cartesian coordinates.
• Minkowski distance: A generalization of the Euclidean and Manhattan distance metrics. Quite often, these metrics can be used interchangeably.
• Cosine similarity: The cosine metric measures the similarity of two data points based on their orientation, as determined by calculating the cosine of the angle between them.

Lastly, for nonnumeric data, you can use metrics like the Jaccard distance metric, an index that compares the number of features that two observations have in common. For example, to illustrate a Jaccard distance, look at these two text strings:

Saint Louis de Ha-ha, Quebec
St-Louis de Ha!Ha!, QC

What features do these text strings have in common? And what features are different between them? The Jaccard metric generates a numerical index value that quantifies the similarity between text strings.

Identifying Clusters in Your Data

You can use many different algorithms for clustering, but the speed and robustness of the k-means algorithm make it a popular choice among experienced data scientists. As alternatives, kernel density estimation methods, hierarchical algorithms, and neighborhood algorithms are also available to help you identify clusters in your dataset.

Clustering with the k-means algorithm

The k-means clustering algorithm is a simple, fast, unsupervised learning algorithm that you can use to predict groupings within a dataset. For getting started with k-means clustering, you first need to be familiar with the concept of centroid. A centroid is the most representative point within any given cluster group. With k-means, you define the number of centroids the model should find as it generates its prediction. The number of centroids is represented by k, and the clusters are formed by calculating the nearest mean values to those centroids, measured by the Euclidean distance between observations.

Because the features of a dataset are usually on different scales, the difference of scales can distort the results of this distance calculation. To avoid this problem, scale your variables before using k-means to predict data groupings.

The quality of the clusters is heavily dependent on the correctness of the k value you specify. If your data is 2- or 3-dimensional, a plausible range of k values may be visually determinable. In the eyeballed approximation of clustering from the World Bank Income and Education data scatterplot (refer to Figure 5-2), a visual estimation of the k value would equate to three clusters, or k = 3.

When defining the k value, it may be possible to choose the number of centroids by looking at a scatterplot (if your dataset is 2- or 3-dimensional) or by looking for obvious, significant groupings within your dataset’s variables. You can pick the number of centroids based on the number of groupings that you know exist in the dataset or by the number of groupings that you want to exist in the dataset. Whatever the case, use your subjective knowledge about the dataset when choosing the number of clusters to be modeled.

If your dataset has more than three dimensions, however, you can use computational methods to generate a good value for k. One such method is the silhouette coefficient — a method that calculates the average distance of each point from all other points in a cluster and then compares that value with the average distance to every point in every other cluster. Luckily, because the k-means algorithm is efficient, it doesn’t require much computer processing power and you can easily calculate this coefficient for a wide range of k values.

The k-means algorithm works by placing sample cluster centers on an n-dimensional plot and then evaluating whether moving them in any single direction would result in a new center with higher density — with more observations closer to it, in other words. The centers are moved from regions of lower density to regions of higher density until all centers are within a region of local maximum density — a true center of the cluster, where each cluster has a maximum number of data points closest to its cluster center. Whenever possible, try to place the centers yourself, manually. If that’s impossible, simply place the centers randomly and run the algorithm several times to see how often you end up with the same clusters.

One weakness of the k-means algorithm is that it may produce incorrect results by placing cluster centers in areas of local minimum density. This happens when centers get lost in low-density regions (in other words, regions of the plot that have relatively few points plotted in them) and the algorithm-driven directional movement (the movement that’s meant to increase point density) starts to bounce and oscillate between faraway clusters. In these cases, the center gets caught in a low-density space that’s located between two high-point density zones. This results in erroneous clusters based around centers that converge in areas of low, local minimum density. Ironically, this happens most often when the underlying data is very well-clustered, with tight, dense regions that are separated by wide, sparse areas.

Get hands-on experience with the free k-means clustering coding demo that’s hosted on the companion website for this book (http://www.businessgrowth.ai/).

To try things out for yourself, start clustering your data with the k-means methods by using either R’s cluster package or Python's Scikit-learn library. For more on R’s cluster package, check out http://cran.r-project.org/web/packages/cluster/cluster.pdf; for more on Scikit-learn, check out http://scikit-learn.org.

Estimating clusters with kernel density estimation (KDE)

If the k-means algorithm doesn’t appeal to you, one alternative way to identify clusters in your data is to use a density smoothing function instead. Kernel density estimation (KDE) is that smoothing method; it works by placing a kernel — a weighting function that is useful for quantifying density — on each data point in the dataset and then summing the kernels to generate a kernel density estimate for the overall region. Areas of greater point density will sum out with greater kernel density, and areas of lower point density will sum out with less kernel density.

Because kernel smoothing methods don’t rely on cluster center placement and clustering techniques to estimate clusters, they don’t exhibit a risk of generating erroneous clusters by placing centers in areas of local minimum density. Where k-means algorithms generate hard-lined definitions between points in different clusters, KDE generates a plot of gradual density change between observations. For this reason, it’s a helpful aid when eyeballing clusters. Figure 5-3 shows what the World Bank Income and Education scatterplot looks like after KDE has been applied.

In Figure 5-3, you can see that the white spaces between clusters have been reduced. When you look at the figure, it’s fairly obvious that you can see at least three clusters, and possibly more, if you want to allow for small clusters.

Clustering with hierarchical algorithms

A hierarchical clustering algorithm is yet another alternative to k-means clustering. In comparison to k-means clustering, the hierarchical clustering algorithm is a slower, clunkier unsupervised clustering algorithm. It predicts groupings within a dataset by calculating the distance and generating a link between each singular observation and its nearest neighbor. It then uses those distances to predict subgroups within a dataset. If you’re carrying out a statistical study or analyzing biological or environmental data, hierarchical clustering might be your ideal machine learning solution.

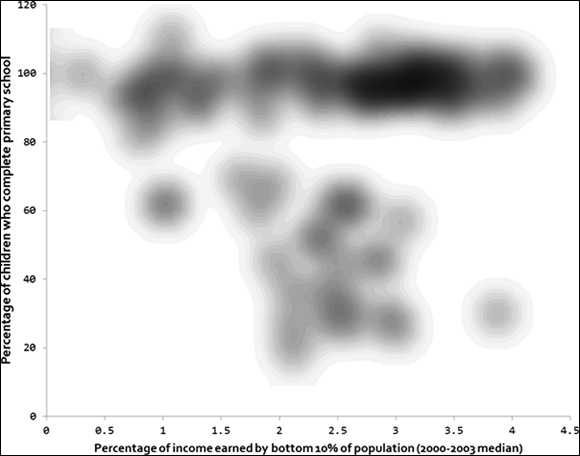
FIGURE 5-3: KDE smoothing of the World Bank’s Income and Education data scatterplot.

To visually inspect the results of your hierarchical clustering, generate a dendrogram — a visualization tool that depicts the similarities and branching between groups in a data cluster. You can use several different algorithms to build a dendrogram, and the algorithm you choose dictates where and how branching occurs within the clusters. Additionally, dendrograms can be built either bottom-up (by assembling pairs of points and then aggregating them into larger and larger groups) or top-down (by starting with the full dataset and splitting it into smaller and smaller groups). Looking at the dendrogram results makes it easier to decide the appropriate number of clusters for your dataset. In the dendrogram example shown in Figure 5-4, the underlying dataset appears to have either three or four clusters.

In hierarchical clustering, the distance between observations is measured in three different ways: Euclidean, Manhattan, or Cosine. Additionally, linkage is formed by three different methods: Ward, Complete, and Average. When deciding what distance and linkage parameters to use, trial-and-error is an easy approach. Just try each combination and then compare all your model results. Go with the model that produces the most accurate prediction.

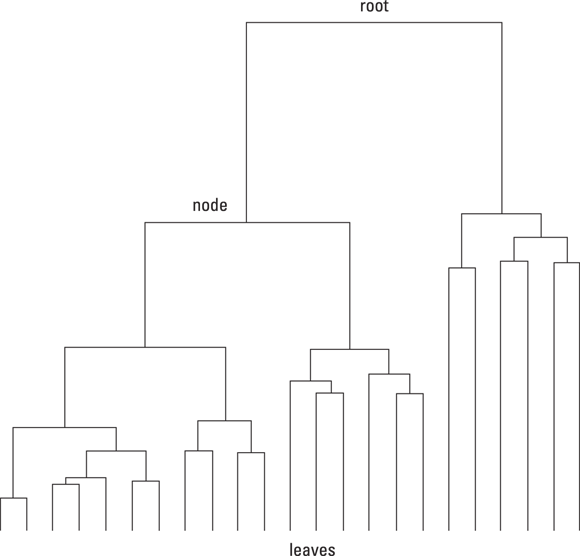
FIGURE 5-4: A schematic layout of a sample dendrogram.

Hierarchical clustering algorithms require more computing resources than k-means algorithms because, with each iteration of hierarchical clustering, many observations must be compared to many other observations. The benefit, however, is that hierarchical clustering algorithms are not subject to errors caused by center convergence at areas of local minimum density (as exhibited with the k-means clustering algorithms).

If you’re working with a large dataset, watch out! Hierarchical clustering will probably be way too slow.

If you want to get started working with hierarchical clustering algorithms, check out R’s hclust package or (again) Python's Scikit-learn library. (If you’re curious about hclust, check out this page:

https://stat.ethz.ch/R-manual/R-patched/library/stats/html/hclust.html

Neither k-means nor hierarchical clustering algorithms perform well when clusters are nonglobular — a configuration where some points in a cluster are closer to points in a different cluster than they are to points in the center of their own cluster. If your dataset shows nonglobular clustering, you can use neighborhood clustering algorithms, like DBScan, to determine whether each point is closer to its neighbors in the same cluster or closer to its neighboring observations in other clusters. (Figure 5-5, in the following section, shows an example of using the DBScan neighborhood clustering algorithm to detect outliers in the classical practice dataset called “Iris,” and the next section covers neighborhood clustering in greater detail.)

Dabbling in the DBScan neighborhood

Density-based spatial clustering of applications with noise (DBScan) is an unsupervised learning method that works by clustering core samples (dense areas of a dataset) while simultaneously demarking noncore samples (portions of the dataset that are comparatively sparse). It’s a neighborhood clustering algorithm that’s ideal for examining two or more variables together to identify outliers. It’s particularly useful for identifying collective outliers — outliers that appear nearby to one another, all having similar values that are anomalous to most values in the variable. (Figure 5-5 shows DBScan at work.)

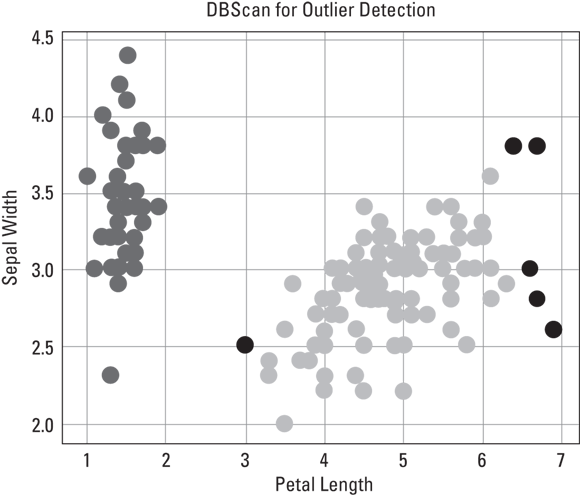
Credit: Python for Data Science Essential Training Part 2, LinkedIn.com

FIGURE 5-5: Using DBScan to detect outliers (in black) within the Iris dataset.

With DBScan, you take an iterative, trial-and-error approach to find the ideal number of outliers for inspection. When experimenting with the DBScan model, outliers should comprise 5 percent or less of the dataset’s observations. You must adjust the model parameters until you’ve isolated this small select group of observations.

Neighborhood clustering algorithms are generally effective, but they are subject to the following two weaknesses:

• Neighborhood clustering can be computationally expensive. With every iteration of this method, every data point might have to be compared to every other data point in the dataset.
• With neighborhood clustering, you might have to provide the model with empirical parameter values for expected cluster size and cluster density. If you guess either of these parameters incorrectly, the algorithm misidentifies clusters, and you must start the whole long process over again to fix the problem. If you choose to use the DBScan method, you’re required to specify these parameters. (As an alternative, you could try the average nearest neighbor and k-nearest neighbor algorithms, which are discussed later in this chapter.)

To avoid making poor guesses for the cluster size and cluster density parameters, you can first use a quick k-means algorithm to determine plausible values.

Categorizing Data with Decision Tree and Random Forest Algorithms

In cases where clustering algorithms fail, decision tree and random forest algorithms might just offer you a perfect alternative machine learning solution. At certain times, you can get stuck trying to cluster and classify data from a nonnumerical dataset. It’s times like these that you can use a decision tree model to help cluster and classify your data correctly.

A decision tree algorithm works by developing a set of yes-or-no rules that you can follow for new data to see exactly how it will be characterized by the model. But you must be careful when using decision tree models, because they run the high risk of error propagation, which occurs whenever one of the model rules is incorrect. Errors are generated in the results of decisions that are made based on that incorrect rule, and then propagated through every other subsequent decision made along that branch of the tree.

To illustrate this type of algorithm, consider a dataset that’s often used in machine learning demonstrations — the list of passenger names from the Titanic. Using a simple decision tree model, you can predict that if a passenger were female or were a male child with a large family, that person probably survived the catastrophe. Figure 5-6 illustrates this determination.

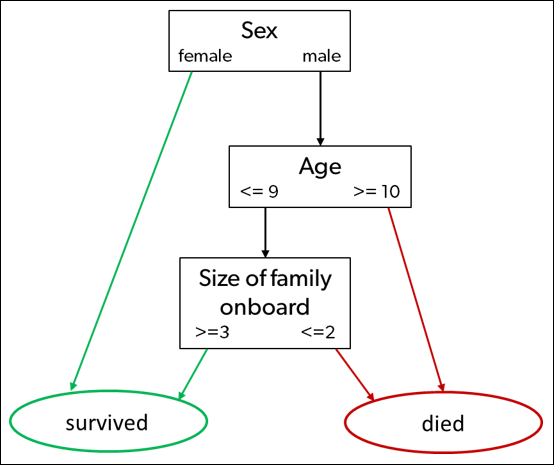
FIGURE 5-6: A decision tree model predicts survival rates from the Titanic catastrophe.

Lastly, random forest algorithms are a slower but more powerful alternative. Rather than build a tree from the data, the algorithm creates random trees and then determines which one best classifies the testing data. This method eliminates the risk of error propagation that is inherent in decision tree models.

Drawing a Line between Clustering and Classification

The purpose of both clustering and classification algorithms is to make sense of, and extract value from, large sets of structured and unstructured data. If you’re working with huge volumes of unstructured data, it only makes sense to try to partition the data into some sort of logical groupings before attempting to analyze it. Both clustering and classification methods allow you to take a sweeping glance of your data all at once and then form some logical structures based on what you find there, before digging deeper into the nuts-and-bolts analysis.

Though your plain-vanilla clustering algorithm — like the k-means method discussed earlier in this chapter — can help you predict subgroups from within unlabeled datasets, there’s way more to life than plain vanilla. I think it’s about time to take things one step further, by exploring how we can make predictions by grouping labeled data instead. Enter instance-based learning classifiers!

Introducing instance-based learning classifiers

Instance-based learning classifiers are supervised, lazy learners — they have no training phase, and they simply memorize training data to predict classifications for new data points. This type of classifier looks at instances — observations within a dataset — and, for each new observation, the classifier searches the training data for observations that are most similar and then classifies the new observation based on its similarity to instances in the training set. Instance-based classifiers include

• k-nearest neighbor (kNN)
• Self-organizing maps
• Locally weighted learning

If you’re unsure about your dataset’s distribution, instance-based classifiers might be a good option, but first make sure that you know their limitations. These classifiers aren’t well-suited for

• Noisy data (data with unexplainable random variation)
• Datasets with unimportant or irrelevant features
• Datasets with missing values

To simplify this introduction as much as possible, I stick to explaining the k-nearest neighbor classification algorithm (known affectionately as kNN). The concepts involved in kNN are a bit tricky, though, so first I introduce you to the simpler average nearest neighbor methods before going into the kNN approach.

Getting to know classification algorithms

You might have heard of classification and thought that it’s the same concept as clustering. Many people do, but this isn’t the case. In classification, your data is labeled, so before you analyze it, you already know the number of classes into which it should be grouped. You also already know which class you want assigned to each data point. In contrast, with clustering methods, your data is unlabeled, so you have no predefined concept of how many clusters are appropriate. You must rely on the clustering algorithms to sort and cluster the data in the most appropriate way.

With classification algorithms, you use what you know about an existing labeled dataset to generate a predictive model for classifying future observations. If your goal is to use your dataset and its known subsets to build a model for predicting the categorization of future observations, you’ll want to use classification algorithms. When implementing supervised classification, you already know your dataset’s labels — the criteria you use to subset observations into classes. Classification helps you see how well your data fits into the dataset’s predefined classes so that you can then build a predictive model for classifying future observations.

Figure 5-7 illustrates how it looks to classify the World Bank’s Income and Education datasets geographically according to continent.

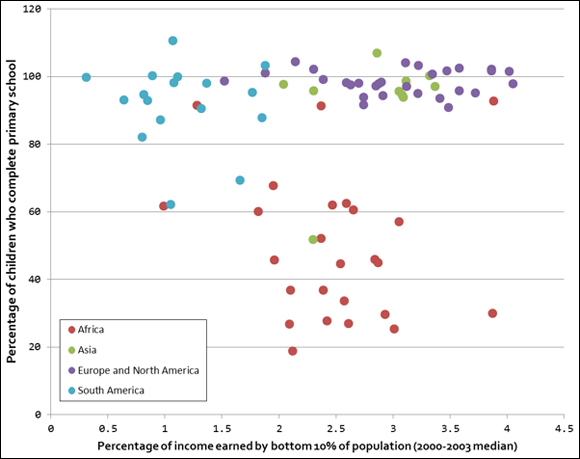
FIGURE 5-7: Using the Continent feature to classify World Bank data.

In Figure 5-7, you can see that, in some cases, the subsets you might identify with a clustering technique do correspond to the Continent category, but in other cases, they don’t. For example, look at the lone Asian country in the middle of the African observations. That’s Bhutan. You could use the data in this dataset to build a model that would predict a Continent class for incoming observations, but if you introduced a data point for a new country that showed statistics similar to those of Bhutan, the new country could be categorized as being part of either the Asian continent or the African continent, depending on how you define your model.

Now imagine a situation in which the original data doesn’t include Bhutan and you use the model to predict Bhutan’s continent as a new data point. In this scenario, the model would incorrectly predict that Bhutan is part of the African continent. This is an example of model overfitting — a situation in which a model is so tightly fit to its underlying dataset, as well as its noise or random error, that the model performs poorly as a predictor for new observations.

To avoid overfitting your models, divide the data into a training set and a test set. A typical ratio is to assign 70 percent (or more) of the data to the training set and the remaining 30 percent to the test set. Build your model with the training set, and then use the test set to evaluate the model by pretending that the test set observations are unknown. You can evaluate the accuracy of your model by comparing the classes assigned to the test set observations to the true classes of these observations.

Model overgeneralization can also be a problem. Overgeneralization is the opposite of overfitting: If you don’t train a machine learning model enough, it will be underfit. As a result, it will make inaccurate, overly general predictions. Naturally it follows that, overly general models end up assigning every class a low degree of confidence. To illustrate model overgeneralization, consider again the World Bank Income and Education datasets. If the model used the presence of Bhutan to cast doubt on every new data point in its nearby vicinity, you end up with a wishy-washy model that treats all nearby points as African, but with a low probability. This model would be a poor predictive performer.

I can illustrate a good metaphor for overfitting and overgeneralization by using this well-known maxim:

If it walks like a duck and talks like a duck, then it’s a duck.

Overfitting would turn the maxim into this statement:

It’s a duck if, and only if, it walks and quacks exactly in the ways that I have personally observed a duck to walk and quack. Since I’ve never observed the way an Australian spotted duck walks and quacks, an Australian spotted duck must not really be a duck at all.

In contrast, overgeneralization would say:

If it moves around on two legs and emits any high-pitched, nasal sound, it’s a duck. Therefore, Fran Fine, who was Fran Drescher’s character in the 1990s American sitcom The Nanny, must be a duck.

Be aware of the constant danger of overfitting and overgeneralization. Find a happy medium between the two.

When classifying data, keep these two points in mind:

• Model predictions are only as good as the model’s underlying data. In the World Bank data example, it could be the case that, if other factors such as life expectancy or energy use per capita were added to the model, its predictive strength would increase.
• Model predictions are only as good as the categorization of the underlying dataset. For example, what do you do with countries, like Russia, that span two continents? Do you distinguish North Africa from sub-Saharan Africa? Do you lump North America in with Europe because they tend to share similar features? Do you consider Central America to be part of North America or South America?

Making Sense of Data with Nearest Neighbor Analysis

At their core, nearest neighbor methods work by taking the value of an observation’s attribute (or feature) — also called an attribute value — and then locating another observation whose attribute value is numerically nearest to it. Because the nearest neighbor technique is a classification method, you can use it to perform tasks as scientifically oriented as deducing the molecular structure of a vital human protein or uncovering key biological evolutionary relationships or as business-driven as designing recommendation engines for e-commerce sites or building predictive models for consumer transactions. The applications are limitless.

A good analogy for the nearest neighbor concept is illustrated in GPS technology. Imagine that you’re in desperate need of a Starbucks iced latte but you have no idea where the nearest store is located. What to do? One easy solution is simply to ask your smartphone where the nearest one is located.

When you do that, the system looks for businesses named Starbucks within a reasonable proximity of your current location. After generating a results listing, the system reports back to you with the address of the Starbucks coffeehouse closest to your current location — the one that is your nearest neighbor, in other words.

As the term nearest neighbor implies, the primary purpose of a nearest neighbor analysis is to examine your dataset and find the observation that’s quantitatively most similar to your observation. Note that similarity comparisons can be based on any quantitative attribute, whether that is distance, age, income, weight, or any other factor that can describe the observation you’re investigating. The simplest comparative attribute is distance.

In my Starbucks analogy, the x, y, z coordinates of the store reported to you by your smartphone are the most similar to the x, y, z coordinates of your current location. In other words, its location is closest in actual physical distance. The quantitative attribute being compared is distance, your current location is the observation, and the reported Starbucks coffeehouse is the most similar observation.

Modern nearest neighbor analyses are almost always performed using computational algorithms. The nearest neighbor algorithm is known as a single-link algorithm — an algorithm that merges clusters if the clusters share between them at least one connective edge (a shared boundary line, in other words). In the following sections, you can learn the basics of the average nearest neighbor algorithm and the k-nearest neighbor algorithm.

Classifying Data with Average Nearest Neighbor Algorithms

Average nearest neighbor algorithms are basic yet powerful classification algorithms. They’re useful for finding and classifying observations that are most similar on average. Average nearest neighbor algorithms are used in pattern recognition, in chemical and biological structural analysis, and in spatial data modeling. They’re most often used in biology, chemistry, engineering, and geosciences.

In this section, you can find out how to use average nearest neighbor algorithms to compare multiple attributes between observations and, subsequently, identify which of your observations are most similar. You can also find out how to use average nearest neighbor algorithms to identify significant patterns in the dataset.

The purpose of using an average nearest neighbor algorithm is to classify observations based on the average of the arithmetic distances between them. If your goal is to identify and group observations by average similarity, the average nearest neighbor algorithm is a useful way to do that.

With respect to nearest neighbor classifiers, a dataset is composed of observations, each of which has an x- and y-variable. An x-variable represents the input value, or feature, and the y-variable represents the data label, or target variable. To keep all these terms straight, consider the following example.

Suppose that your friendly neighborhood business analyst, Business Analyst Stu, is using average nearest neighbor algorithms to perform a classification analysis of datasets in his organization’s database. Stu is comparing employees based on the following five features:

• Age
• Number of children
• Annual income
• Seniority
• Eligibility to Retire

Shown below, you can see that each employee in Stu’s organization is represented by a 5-dimensional tuple — a finite ordered list (or sequence).

• Employee Mike: (34, 1, 120000, 9, 0)
• Employee Liz: (42, 0, 90000, 5, 0)
• Employee Jin: (22, 0, 60000, 2, 0)
• Employee Mary: (53, 3, 180000, 30, 1)

These tuples were created from the data in the dataset that’s shown in Table 5-1 below. Each tuple consists of data on the following five features: Age, Number of Children, Annual Income, and Seniority as predictive features, Business Analyst Stu calculates the average arithmetic differences between each of the employees. Figure 5-8 shows the calculated distances between each of the employees.

TABLE 5-1: Business Analyst Stu’s Employee Data

Employee Name	Age	Number of Children	Annual Income	Seniority	Eligible to Retire
Mike	34	1	$120,000	9	0
Liz	42	0	$90,000	5	0
Jin	22	0	$60,000	2	0
Mary	53	3	$180,000	30	1

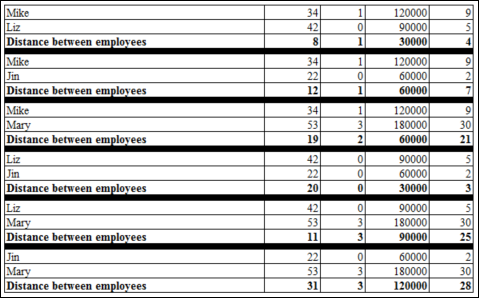
FIGURE 5-8: The distances between the employees’ tuples.

After Business Analyst Stu has this arithmetic measure of distance between the employees, he finds the average nearest neighbor by taking an average of these separation distances. Figure 5-9 shows that average similarity.

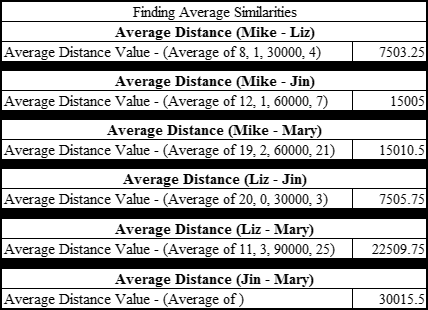
FIGURE 5-9: Finding the average similarity between employees.

Stu then groups the employees by the average separation distance between them. Because the average separation distance values between Mike, Liz, and Jin are the smallest, they’re grouped into class 0. Mary’s average separation distances are quite unlike the others, so she is put into her own class — Class 1.

Does this make sense? Well, you’re working with a labeled dataset and you can see that the attribute Eligible to Retire assumes only one of two possible values. So, yes. If the algorithm predicts two classifications within the data, that’s a reasonable prediction. Furthermore, if Stu gets new incoming data points that are unlabeled with respect to a person’s eligibility to retire, he could probably use this algorithm to predict for that eligibility, based on the other four features.

Classifying with K-Nearest Neighbor Algorithms

The best way to define a k-nearest neighbor is to call it a supervised machine learning classifier that uses the observations it memorizes from within a test dataset to predict classifications for new, unlabeled observations. kNN makes its predictions based on similarity — the more similar the training observations are to the new, incoming observations, the more likely it is that the classifier will assign them both the same class. kNN works best if the dataset is

• Low on noise
• Free of outliers
• Labeled
• Composed only of relevant selected features
• Composed of distinguishable groups

If you’re working with a large dataset, you may want to avoid using kNN, because it will probably take way too long to make predictions from larger datasets.

Over on the companion website to this book (http://www.businessgrowth.ai/), you’ll find a free training-and-coding demonstration of how to build a quick-and-easy k-nearest neighbor classifier in Python.

In the larger context of machine learning, kNN (like all instance-based learning classifiers) is known as a lazy machine learning algorithm — in other words, it has little to no training phase. It simply memorizes training data and then uses that information as the basis on which to classify new observations. The goal of the kNN is to estimate the class of the query point P based on the classes of its k-nearest neighbors.

The kNN algorithm is a generalization of the nearest neighbor algorithm. Rather than consider the nearest neighbor, you consider k numbers of nearest neighbors from within a dataset that contains n number of data points — k defines how many nearest neighbors will have an influence on the classification process. In kNN, the classifier classifies the query point P per the classification labels found in a majority of k-nearest points surrounding the query point.

If you know little about the distribution of your dataset, kNN is definitely a good classification method for you to use. What’s more, if you do have a solid idea about your dataset’s distribution and feature selection criteria — the criteria you're using to identify and remove noise in the dataset — you can leverage this information to create significant enhancements in the algorithm’s performance.

Even though kNN is among the simplest and most easy-to-implement classification methods, it nevertheless yields competitive results when compared to some of the more sophisticated machine learning methods. Probably because of its simplicity and the competitive results it provides, the kNN algorithm has been ranked among the top ten most influential data mining algorithms by the academic research community.

Understanding how the k-nearest neighbor algorithm works

To use kNN, you simply need to pick a query point — usually called P — in the sample dataset and then compute the k-nearest neighbors to this point. The query point P is classified with a label that’s the same as the label of most k-nearest points that surround it. (Figure 5-10 gives a bird’s-eye view of the process.)

K-nearest neighbors are quantified by either distance or similarity based on another quantitative attribute.

Consider the following example: A dataset is given by [1, 1, 4, 3, 5, 2, 6, 2, 4], and point P is equal to 5. Figure 5-10 shows how kNN would be applied to this dataset. By specifying that k is equal to 3, the figure shows that, based on distance, there are three nearest neighbors to the point 5. Those neighbors are 4, 4, and 6. So, based on the kNN algorithm, query point P will be classified as 4 because 4 is the majority number in the k number of points nearest to it. Similarly, kNN continues defining other query points using the same majority principle.

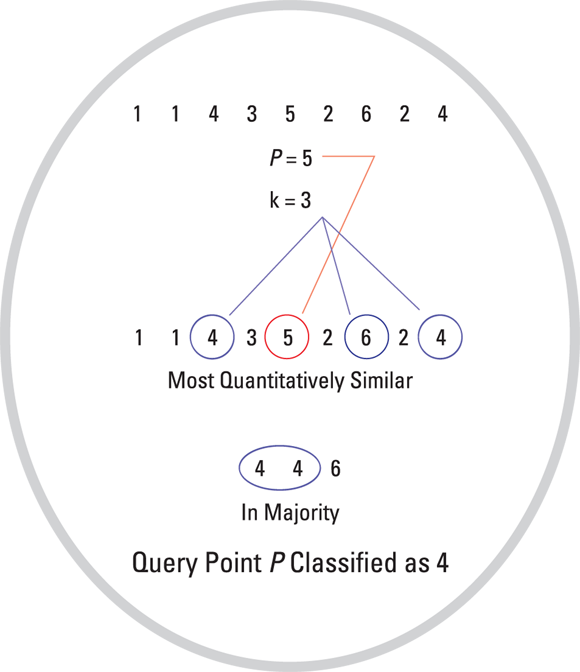
FIGURE 5-10: How kNN works.

When using kNN, it’s crucial to choose a k value that minimizes noise — unexplainable random variation, in other words. At the same time, you must choose a k value that includes sufficient data points in the selection process. If the data points aren’t uniformly distributed, it’s generally harder to predetermine a good k value. Be careful to select an optimum k value for each dataset you’re analyzing.

Large k values tend to produce less noise and more boundary smoothing — clearer definition and less overlap — between classes than small k values do.

Knowing when to use the k-nearest neighbor algorithm

kNN is particularly useful for multi-label learning — supervised learning where the algorithm is applied so that it automatically learns from (detects patterns in) multiple sets of instances. Each of these sets could potentially have several classes of their own. With multi-label learning, the algorithm learns to predict multiple class labels for each new instance it encounters.

The problem with kNN is that it takes a lot longer than other classification methods to classify a sample. Nearest neighbor classifier performance depends on calculating the distance function as well as on the value of the neighborhood parameter k. You can try to speed things up by specifying optimal values for k and n.

Exploring common applications of k-nearest neighbor algorithms

kNN is often used for Internet database management purposes. In this capacity, kNN is useful for website categorization, web page ranking, and other user dynamics across the web.

kNN classification techniques are also quite beneficial in customer relationship management (CRM), a set of processes that ensure a business sustains improved relationships with its clients while simultaneously experiencing increased business revenues. Most CRMs gain tremendous benefit from using kNN to data-mine customer information to find patterns that are useful in boosting customer retention.

The method is so versatile that even if you’re a small-business owner or a marketing department manager, you can easily use kNN to boost your own marketing return on investment. Simply use kNN to analyze your customer data for purchasing patterns, and then use those findings to customize marketing initiatives so that they’re more exactly targeted for your customer base.

Solving Real-World Problems with Nearest Neighbor Algorithms

Nearest neighbor methods are used extensively to understand and create value from patterns in retail business data. In the following sections, I present two powerful cases where kNN and average-NN algorithms are being used to simplify management and security in daily retail operations.

Seeing k-nearest neighbor algorithms in action

Techniques associated with k-nearest neighbor algorithms are often used for theft prevention in the modern retail business. Of course, you’re accustomed to seeing CCTV cameras around almost every store you visit, but most people have no idea how the data gathered from these devices is being used.

You might picture someone in the back room resolutely monitoring these cameras for suspicious activity for hours at a time, and perhaps that is how things were done in the past. But now a modern surveillance system is intelligent enough to analyze and interpret video data on its own, without the need for human assistance. The modern systems can now use k-nearest neighbor for visual pattern recognition to scan and detect hidden packages in the bottom bin of a shopping cart at checkout. If an object is detected that is an exact match with an object listed in the database, the price of the spotted product can even automatically be added to the customer’s bill. Though this automated billing practice isn’t used extensively now, the technology has been developed and is available for use.

Retail stores also use k-nearest neighbor to detect patterns in credit card use. Many new transaction-scrutinizing software applications use kNN algorithms to analyze register data and spot unusual patterns that indicate suspicious activity. For example, if register data indicates that a lot of customer information is being entered manually rather than by automated scanning and swiping, it can indicate that the employee who’s using that register is in fact stealing a customer’s personal information. Or, if register data indicates that a particular good is being returned or exchanged multiple times, it can indicate that employees are misusing the return policy or trying to make money from making fake returns.

Seeing average nearest neighbor algorithms in action

Average nearest neighbor algorithm classification and point pattern detection can be used in grocery retail to identify key patterns in customer purchasing behavior, and subsequently increase sales and customer satisfaction by anticipating customer behavior. Consider the following story:

As with other grocery stores, buyer behavior at (the fictional) Waldorf Food Co-op tends to follow fixed patterns. Managers have even commented on the odd fact that members of a particular age group tend to visit the store during the same particular time window, and they even tend to buy the same types of products. One day, Manager Mike became extremely proactive and decided to hire a data scientist to analyze customer data and provide exact details about some recent trends that were noticeably odd. Data Scientist Dan got in there and quickly uncovered a pattern among employed middle-aged male adults: They tended to visit the grocery store only during the weekends or at the end of the day on weekdays, and if they entered the store on a Thursday, they almost always bought beer.

Armed with these facts, Manager Mike quickly used this information to maximize beer sales on Thursday evenings by offering discounts, bundles, and specials. Not only was the store owner happy with the increased revenues, but Waldorf Food Co-op’s male customers were also happy because they got more of what they wanted, when they wanted it.