THE CLIMATE OF OPINION IN REFORMATION EUROPE, BOTH RELIgious and intellectual, was unfavorable for the acceptance of the Copernican heliocentric theory, which was opposed by both the Catholic and the Protestant churches as well as scholastic philosophers in the universities, who held firmly to the geocentric cosmology of Aristotle and Ptolemy.
The gradual acceptance of the Copernican theory was due primarily to its success in giving an accurate mathematical description of the motion of the celestial bodies. His sun-centered cosmology, by contrast, was in most cases either ignored or rejected outright. The gradual acceptance of his theories was due to their use in new astronomical tables that were more successful in predicting celestial motion than the old ones based on the Ptolemaic theory.
The first astronomical tables based on the Copernican theory were courtesy of Erasmus Reinhold (1511–1553), professor of astronomy at the University of Wittenberg at the same time as Rheticus. When Rheticus returned to Wittenberg in September 1541 with the manuscript of De revolutionibus, he likely showed it to Reinhold. The following year Reinhold published his commentary on Peurbach’s Theoricae novae planetarum, in which he wrote of Copernicus in the preface: “I know of a modern scientist who is exceptionally skillful. He has raised a lively expectancy in everybody. One hopes that he will restore astronomy.” Later he wrote, “I hope that this astronomer, whose genius all posterity will rightly admire, will at long last come to us from Prussia.”
Reinhold set out to produce a more extensive version of the planetary tables in De revolutionibus, which were published in 1551 as the Prutenic Tables, where in the introduction he praises Copernicus but is silent about his heliocentric theory. Reinhold also wrote a commentary on De revolutionbus, but it was unfinished when he died of the plague in 1553.
The Prutenic Tables were the first complete planetary tables prepared in Europe for three centuries. They were demonstrably superior to the older tables, which were now out of date, and so they were used by most astronomers, lending legitimacy to the Copernican theory even when those who used them did not acknowledge the sun-centered cosmology of Copernicus. As the English astronomer Thomas Blundeville wrote in the preface to an astronomy text in 1594: “Copernicus … affirmeth that the earth turneth about and that the sun standeth still in the midst of the heavens, by help of which false supposition he hath made truer demonstrations of the motions and revolutions of the celestial spheres, than ever were made before.”
The English mathematician Robert Recorde (1510–1558) was one of the first to lend some support to the Copernican theory. He discusses the theory in his Castle of Knowledge (1551), an elementary text on Ptolemaic astronomy with a brief favorable reference to the Copernican theory. It is written in the form of a dialogue between a master and a scholar concerning Ptolemy’s arguments against the earth’s motion. After the scholar sums up these arguments, the master presents the Copernican theory in a very positive manner.
That is trulye to be gathered: howe be it, COPERNICUS, a man of greate learning, of much experience, and of wonderfull diligence in observation, hath renewed the opinion of ARISTARCHUS SAMIUS, and affirmith that the earthe not only moveth circularlye about his own centre, but also may be, yea and is, continually out of the precise centre of the world 38 hundred thousand miles.
Five years later an Ephemeris, or set of astronomical tables, was printed in London for the year 1557 by John Feild, based on the work of Copernicus and Reinhold. The introduction was written by John Dee (1527–1608), Queen Elizabeth’s astrologer, who noted that he had persuaded Feild to compile the Ephemeris, based on the Copernican theory, since the older tables were no longer satisfactory. Dee praised Copernicus for his “more than Herculean” effort in restoring astronomy, though he said that this was not the place to discuss the heliocentric theory itself.
A second edition of De revolutionibus was published in Basel in 1566, and copies of it made their way to Italy and England. The English astronomer Thomas Digges (c. 1546–1595), a pupil of Dee, obtained a copy of De revolutionibus that has survived in the library of Geneva University, along with a note he wrote on the title page, “Vulgi opinio Error” (“the common opinion errs”), indicating that he was one of the few sixteenth-century scholars who accepted the Copernican theory.
Digges had already published a work on the nova or new star of 1572. (It is now known that a nova is a star that explodes at the end of its evolutionary cycle, releasing an enormous amount of energy for a few months.) He hoped to use his observations to confirm or refute the Copernican theory, and he appealed to other astronomers to help him.
Digges did a free English translation of chapters 9 through 11 of the first book of De revolutionibus, adding it to his father’s perpetual almanac, A Prognostication Everlasting, publishing them together in 1576 as a Perfit Description of the Caelestiall Orbes, according to the most ancient doctrines of the Pythagoreans lately revived by Copernicus and by Geometricall Demonstrations approved. Digges stated that he had included this excerpt from De revolutionibus in the almanac “so that Englishmen might not be deprived of so noble a theory.”
The book was accompanied by a large folded map of the sun-centered universe, in which the stars were not confined to the outermost celestial sphere but scattered outward indefinitely in all directions. Digges thus burst the bounds of the medieval cosmos, which till then had been limited by the ninth celestial sphere, the one containing the supposedly fixed stars, which in his model extended to infinity.

A model of the Copernican system from Thomas Digges’s A Prognostication Everlasting, 1576
The geocentric celestial spheres were still very much a part of the general worldview in late-sixteenth-century England, as is evident from Christopher Marlowe’s play, The Tragical History of Dr. Faustus. As soon as Faustus has made his pact with the devil, he begins to question Mephistopheles about matters beyond the ken of mortals, beginning with the celestial spheres.
Speak, are there many spheres above the moon?
Are all celestial bodies but one globe,
As is the substance of this centric earth?
The concept of an infinite universe was one of the revolutionary ideas for which the Italian mystic Giordano Bruno (1548–1600) was condemned by the Catholic Church, which had him burned at the stake in Rome on February 17, 1600. Bruno expressed his belief in the Copernican theory on several occasions, most notably in a lecture he gave at Oxford in 1583. Historian Frances A. Yates describes Bruno’s mystical interpretation of the theory, in which he was encouraged by the reference that Copernicus had made to Hermes Trismegistus:
In his defense of Copernicanism against the Aristotelians of Oxford, Bruno presented Copernicus “only as a mathematician” who had not appreciated the true inwardness of his discovery as he, Bruno, understood it—as portending a return to magical insight into living nature. In support of the movement of the earth, Bruno quoted a passage from one of the treatises of the Corpus Hermeticum, which states that the earth moves because it is alive.
Yates went on to say that “the legend that the nineteenth century built around Bruno as the hero who, unlike Galileo, refused to retract his belief that the earth moves is entirely without foundation. Bruno’s case, however, may have affected the attitude of the Church toward the Copernican hypothesis, and may have encouraged the Inquisition’s suspicion of Galileo.”
At the beginning of his dialogue on The Infinite Universe and the Worlds, published in 1584, Bruno said, through one of his characters, that in this limitless space there are innumerable worlds similar to our earth, each of them revolving around its own star-sun. “There are then innumerable suns, and an infinite number of earths revolve around these suns, just as the seven [the five visible planets plus the earth and its moon] we can observe revolve around this sun which is close to us.”
Bruno’s universe was not only infinite but dynamic, in contrast to the finite cosmos of Aristotle, for whom the celestial region was immutable. Here Bruno took his inspiration from the atomic theory of Democritus and Epicurus as interpreted by Lucretius in his De rerum natura, which had been rediscovered in 1417. According to Bruno, the living universe is limited neither in its extent nor in its constantly changing multiplicity:
There are no ends, boundaries, limits or walls which can defraud or deprive us of the infinite multitude of things.… Thus Democritus and Epicurus, who maintained that everything throughout infinity suffered renewal and restoration, understood these matters more truly than those who at all costs maintain a belief in the immutability of the Universe, alleging a constant and unchanging number of particles of identical material that perpetually undergo transformation, one into another.
The concept of an infinite universe appears also in the work of the English scientist William Gilbert (1544–1603), who may have been influenced in this regard by Thomas Digges and Giordano Bruno. Gilbert’s De magnete, published in 1600, was the first work on magnetism since that of Petrus Peregrinus in the thirteenth century.
The sixth and final book of De magnete was devoted to Gilbert’s cosmological theories, in which he rejected the crystalline celestial spheres of Aristotle and said that the apparent diurnal rotation of the stars was actually due to the axial rotation of the earth, which he believed to be a huge magnet. His rejection of diurnal stellar motion was based on his belief that the stars were limitless in number and extended to infinity, so that it was thus ridiculous to assume that they rotated nightly around the celestial pole. While Gilbert discussed the motions of the earth according to Copernicus and Giordano Bruno, he did not affirm or deny the heliocentric theory; at times he dismissed it as not being pertinent to the topic he was discussing.
Meanwhile astronomy was being revolutionized by the Danish astronomer Tycho Brahe (1546–1601), who in the last quarter of the seventeenth century made systematic observations of significantly greater accuracy than any ever done in the past, all just before the invention of the telescope.
Tycho, born to a noble Danish family, was brought up by his paternal uncle, Jörgen Brahe, who hired a tutor to teach him Latin and the preparatory subjects for a university education. He enrolled at the University of Copenhagen at the age of thirteen and subsequently continued his studies at the universities of Leipzig, Rostock, and Basel, from which he graduated in 1568. The astronomy books that he studied included Sacrobosco’s De sphaera, which had been in use since the thirteenth century, and other texts based on the homocentric spheres of Aristotle and the epicycles and eccentrics of Ptolemy.
There had been an eclipse of the moon on October 28, 1566, that led Tycho to predict the death of the Ottoman sultan Süleyman the Magnificent, who, as they soon learned, had already died on September 6 of that year. On December 29 Tycho’s third cousin, Manderup Parsburg, mocked him about this at a dinner party and they both drew their swords and went outside to duel. Before the other guests could stop them, Parsburg had lopped off a large part of Tycho’s nose, which, after a long convalescence, he replaced with an artificial nose of gold and silver blended to appear flesh colored. The disfigurement is apparent in the portrait of Tycho that appears in his book Astronomiae instauratae mechanica, published in 1598.
The occurrence of a solar eclipse on August 21, 1560, though only partial in Copenhagen, aroused Tycho’s interest in observational astronomy, which was not part of the university curriculum. He immediately obtained a copy of a set of ephemerides, or planetary tables, based on Reinhold’s Prutenic Tables. Here he first became aware of the work of Copernicus, whom he called “a second Ptolemy.” Tycho made an observation in Leipzig in August 1563 that he considered to be a turning point in his career, when he noted a conjunction of Saturn and Jupiter, measuring the angular distance between the two planets using a pair of compasses. He found that the Alphonsine Tables were a month off in predicting the date of the conjunction, and that the Prutenic Tables were several days in error. He began making observations with a homemade instrument known as a radius or cross-staff, and since it was not very accurate, he devised a table of corrections to make up for its deficiencies.
Early in 1569 Tycho went to Augsburg, in Germany, where he made his first observation on April 14. The instruments that he designed and built for his observations included a great quadrant with a radius of some nineteen feet for measuring the altitude of celestial bodies. He also constructed a huge sextant with a radius of fourteen feet for measuring angular separations, as well as a celestial globe ten feet in diameter on which to mark the positions of the stars in the celestial map that he began to create.
Tycho returned to Denmark in 1570 and, after his father’s death on May 9 of the following year, he moved to Herrevad Abbey, the home of his maternal uncle, Steen Bille, where he spent his time performing alchemical experiments. The following year he entered a common-law marriage with Kirsten Jorgensdatter, the daughter of the local pastor, who was to bear him six children.
On November 11, 1572, as Tycho was walking back to supper from his laboratory, he saw a nova, or new star, that had suddenly appeared in the constellation Cassiopeia, exceeding even the planet Venus in its brilliance. As he later wrote in his tract on the nova: “I knew perfectly well—for from my earliest youth I have known all the stars in the sky, something which one can learn without difficulty—that no star had ever existed in that place in the heaven, not even the very tiniest, to say nothing of a star of such striking clarity.”
Tycho’s measurements indicated that the nova was well beyond the sphere of Saturn, and the fact that its position did not change showed that it was not a comet. This was clear evidence of a change taking place in the celestial region, where, according to Aristotle’s doctrine, everything was perfect and immutable.
The nova eventually began to fade, its color changing from white to yellow and then red, finally disappearing from view in March 1574. By then Tycho had written a brief tract entitled De nova stella (The New Star), which was published in Copenhagen in May 1573. After presenting the measurements that led him to conclude that the new star was in the heavens beyond the planetary spheres, Tycho expressed his amazement at what he had observed. “I doubted no longer,” he wrote. “In truth, it was the greatest wonder that has ever shown itself in the whole of nature since the beginning of the world, or in any case as great as [when the] Sun was stopped by Joshua’s prayers.”
The tract impressed King Frederick II of Denmark, who gave Tycho an annuity along with the small offshore island of Hveen, in the Oresund Strait north of Copenhagen, the revenues of which would enable him to build and equip an observatory. Tycho settled on Hveen in 1576, calling the observatory Uraniborg, meaning “City of the Heavens.” The astronomical instruments and other equipment of what came to be a large research center were so numerous that Tycho was forced to build an annex called Stjernborg, “City of the Stars,” with subterranean chambers to shield the apparatus and researchers from the elements. That same year Tycho and his assistants began a series of observations of unprecedented accuracy and precision that would continue for the next two decades, laying the foundations for what would prove to be the new astronomy.
Tycho’s main project at Uraniborg was to make new and more accurate determinations of the celestial coordinates of the fixed stars, and to observe the changing positions of the sun, moon, and planets for the purpose of improving the theories of their motions. He produced a catalogue giving the coordinates of 777 fixed stars, to which he later added another 223 so as to bring the total to 1,000.
The celestial coordinates given in Tycho’s star catalogue had a mean error, compared to modern values, of less than 40 seconds of arc, far less than that of any of his predecessors. Comparing the coordinates of the twenty-one principal stars in his catalogue with those measured from antiquity up to his own time, Tycho computed a value for the rate of precession of the equinoxes equal to 51 seconds of arc per year, as compared to the modern value of 50.23 seconds. He correctly assumed the precession to be uniform, making no mention of the erroneous Islamic trepidation theory that had caused unnecessary problems for Copernicus.
Shortly after sunset on November 13, 1577, Tycho first noticed a spectacular comet with a very long tail, and he continued to observe it nightly until January 26 of the following year, by which time it had faded to the point that it was hardy visible. His detailed observations of the comet led him to conclude that at its closest approach it had been farther away than the moon, in fact even beyond the orbit of Mercury, and that it was in an oval orbit around the sun among the outer planets. This contradicted the Aristotelian doctrine that comets were meteorological phenomena occurring below the sphere of the moon. Tycho was thus led to reject Aristotle’s concept of the homocentric crystalline spheres, and he concluded that the planets were moving independently through space.
There really are not any spheres in the heavens.… Those which have been devised by the experts to save the appearances exist only in the imagination for the purpose of enabling the mind to conceive the motion which the heavenly bodies trace in their course and, by the aid of geometry, to determine the motion numerically through the use of arithmetic.
Despite his admiration for Copernicus, Tycho rejected the heliocentric theory, both on physical grounds and on the absence of stellar parallax, where in the latter case he did not take into account the argument made by Archimedes and Copernicus that the stars were too far away to show any parallactic shift. Tycho rejected both the diurnal rotation of the earth and its annual orbital motion, retaining the Aristotelian belief that the stars rotated nightly around the celestial pole.
Faced with the growing debate between the Copernican and Ptolemaic theories, Tycho proposed his own planetary model, which combines elements of the geocentric and heliocentric theories. In the Tychonic system the immobile earth is still at the center of the universe, with the sphere of the fixed stars revolving around it in twenty-four hours. The other planets were in orbit around the sun, which circled the earth every twenty-four hours, while the moon went around the earth once a month. The orbits of Mercury and Venus intersected the orbit of the sun at two points, but did not encompass the earth. The orbit of Mars also intersected the sun’s orbit in two places, but enclosed the earth and its orbiting moon. The orbits of Jupiter and Saturn enclosed the entire path of the sun. Tycho believed that his model combined the best features of both the Ptolemaic and Copernican theories, since it kept the earth stationary and explained why Mercury and Venus were never very far from the sun.
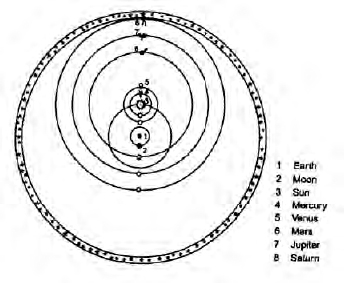
The Tychonic model for planetary motion
Tycho’s patron Frederick II died in 1588 and was succeeded by his son Christian IV, who was then eleven years old. When Christian came of age, in 1596, he informed Tycho that he would no longer support his astronomical research. Without financial backing, Tycho was forced to abandon Uraniborg the following year, taking with him all of his astronomical instruments and records, hoping to find a new royal patron.
Tycho moved first to Copenhagen and then in turn to Rostock and Wandsburg Castle, outside Hamburg. He remained for two years at Wandsburg Castle, where in 1598 he published his Astronomiae instauratae mechanica, a description of all his astronomical instruments. He sent copies of his treatise to all of the wealthy and powerful people who might be interested in supporting his further researches. He appended his star catalogue to the copy he presented to the emperor Rudolph II, who agreed to support Tycho’s work, appointing him as the court astronomer.
Thus in 1600 Tycho moved to Prague, where he set up his instruments and created a new observatory at Benatky Castle, several miles northeast of the city. Soon afterward he hired an assistant named Johannes Kepler (1571–1630), a young German mathematician who had sent him an interesting treatise on astronomy, the Mysterium cosmographicum.
Kepler was born on December 27, 1571, in Weil der Stadt in southwestern Germany. His father was an itinerant mercenary soldier, his mother a fortune-teller who at one point was accused of being a witch and almost burned at the stake. The family moved to the nearby town of Lemberg, where Kepler was enrolled in one of the excellent Latin schools founded by the Duke of Württemberg. Kepler’s youthful interest in astronomy had been stimulated by seeing the comet of 1577 and a lunar eclipse in 1580.
In 1589 Kepler entered the University of Tübingen, where, in addition to his studies in mathematics, physics, and astronomy, he was influenced by Platonism, Pythagoreanism, and the cosmological ideas of Nicholas of Cusa. His mathematics lectures were based on the works of Euclid, Archimedes, and Apollonius of Perge. (As Kepler later said, “How many mathematicians are there, who would toil through the Conics of Apollonius of Perge?”)
Kepler was particularly influenced by his professor of astronomy, Michael Maestlin, from whom he first learned of the heliocentric theory. In the introduction to his first book, the Mysterium cosmographicum, Kepler wrote of his excitement on discovering the work of Copernicus, which he described as “a still unexhausted treasure of truly divine insight into the magnificent order of the whole world and of all bodies.” He wrote also of how Copernicus inspired him to begin thinking about the causes behind this cosmic order:
When I was studying under the distinguished Michael Maestlin at Tübingen six years ago, seeing the inconveniences of the commonly accepted theory of the universe, I became so delighted with Copernicus, whom Maestlin often mentioned in his lectures, that I often defended his opinions in the students’ debates about physics. I even wrote a painstaking disputation about the first motion, maintaining that it happens because of the rotation of the earth. I have by degrees—partly out of hearing Maestlin, partly by myself—collected all the advantages that Copernicus has over Ptolemy. At last in the year 1595 in Graz when I had an intermission in my lectures, I pondered on the subject with the whole energy of my mind. And there were three things above all for which I sought the causes as to why it was this way and not another—the number, the dimensions, and the motion of the orbs.
Kepler received his master’s degree in Tübingen in 1591, after which he studied theology there until 1594, when he was appointed teacher of mathematics at the Protestant seminary in the Austrian town of Graz. A year after his arrival in Graz, Kepler developed an idea that he thought explained the arrangement and order of the heliocentric planetary system. He had learned from his reading of Euclid that there were five and only five regular polyhedra, the so-called Platonic solids, in which all of the faces are equal as well as equilateral—the cube, tetrahedron, dodecahedron, icosahedron, and octahedron—and it occurred to him that they were related to the orbits of the earth and the five other planets. He explained the scheme in his treatise, the Mysterium cosmographicum, published in 1596:
The earth’s orbit is the measure of all things; circumscribe around it a dodecahedron, and the circle containing it will be Mars; circumscribe around Mars a tetrahedron, and the circle containing this will be Jupiter; circumscribe around Jupiter a cube, and the circle containing this will be Saturn. Now inscribe within the earth an icosahedron, and the circle contained in it will be Venus; inscribe within Venus an octahedron, and the circle contained in it will be Mercury. You now have the reason for the number of planets.
The values that Kepler calculated for the relative radii of the planetary orbits agree fairly well with those determined by Copernicus, when allowances are made for the eccentricities of the orbits. Also, in the case of Mercury, Kepler compromised by taking the radius of a sphere formed by the edges of the octahedron rather than in the octahedron itself, though there was no physical basis for his theory. With these concessions everything agrees within 5 percent, except for Jupiter, where the Kepler’s value is off by 9 percent, at which, as he writes, “no one will wonder, considering such a great distance.”
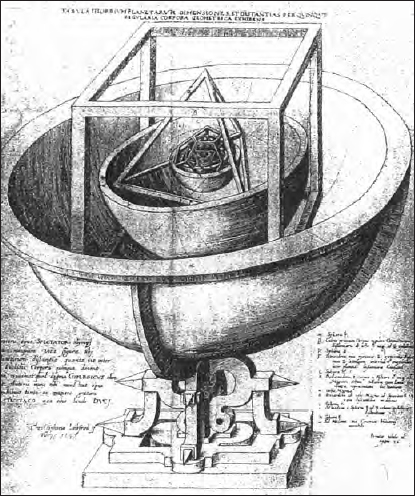
Drawing of the nested Platonic bodies from the Mysterium cosmographicum
Kepler sent copies of his treatise to a number of scientists, including Galileo Galilei (1564–1642). In his letter of acknowledgment, dated August 4, 1597, Galileo congratulated Kepler for having had the courage, which he himself lacked, of publishing a work supporting the Copernican theory. Kepler wrote back to Galileo on October 13, 1597, encouraging him to continue supporting the Copernican theory. “Have faith, Galilei, and come forward!” he wrote. “If my guess is right, there are but few of the prominent mathematicians of Europe who would wish to secede from us: such is the power of truth.”
Kepler had also sent a copy of the Mysterium cosmographicum to Tycho Brahe, who received it after he had left Denmark for Germany. Tycho responded warmly, calling the treatise “a brilliant speculation,” beginning a correspondence that eventually led Kepler to accept Tycho’s invitation to join him at his new observatory at Benatky. As Tycho wrote in response to Kepler’s letter of acceptance: “You will come not so much as a guest but as a very welcome friend and highly desirable participant and companion in our observations of the heavens.”
Kepler finally arrived at Benatky with his family early in 1600, beginning a brief but extraordinarily fruitful collaboration with Tycho. When Kepler began work at Benatky he had hopes that he could take Tycho’s data and use it directly to check his own planetary theory. But he was disappointed to find that most of Tycho’s data was still in the form of raw observations, which first had to be subjected to mathematical analysis. Moreover, Tycho was extremely possessive of his data and would not reveal any more of it than Kepler needed for his work.
These and other disagreements with Tycho led Kepler to leave Benatky in April of that year, though he returned in October after considerable negotiation concerning the terms of his employment. Tycho then assigned Kepler the task of analyzing the orbit of Mars, which up to that time had been the responsibility of his assistant, Longomontanus, who had just resigned. Kepler later wrote: “I consider it a divine decree that I came at exactly the time when Longomontanus was busy with Mars. Because assuredly either through it we arrive at the knowledge of the secrets of astronomy or else they remain forever concealed from us.”
Mars and Mercury are the only visible planets with eccentricities large enough to make their orbits significantly different from perfect circles. But Mercury is so close to the sun that it is difficult to observe, leaving Mars as the ideal planet for checking a mathematical theory, which is why Kepler was so enthusiastic at being able to analyze its orbit.
Early in the autumn of 1601 Tycho brought Kepler to the imperial court and introduced him to the emperor Rudolph. Tycho then proposed to the emperor that he and Kepler compile a new set of astronomical tables. With the emperor’s permission, this would be named the Rudolphine Tables, and since it was to be based on Tycho’s observations it would be more accurate than any done in the past. The emperor graciously consented and agreed to pay Kepler’s salary in this endeavor.
Soon afterward Tycho fell ill, and after suffering in agony for eleven days, he died on October 24, 1601. On his deathbed he made Kepler promise that the Rudolphine Tables would be completed, and he expressed his hopes that it would be based on the Tychonic planetary model. As Kepler later wrote of Tycho’s final conversation with him: “Although he knew I was of the Copernican persuasion, he asked me to present all my demonstrations in conformity with his hypothesis.”
Two days after Tycho’s death the emperor Rudolph appointed Kepler as court mathematician and head of the observatory at Benatky. Kepler thereupon resumed his work on Mars, now with unrestricted access to all of Tycho’s data. At first he tried the traditional Ptolemaic methods—epicycle, eccentric, and equant—but no matter how he varied the parameters, the calculated positions of the planet disagreed with Tycho’s observations by up to 8 minutes of arc. His faith in the accuracy of Tycho’s data led him to conclude that the Ptolemaic theory of epicycles, which had been used by Copernicus, would have to be replaced by a completely new theory, as he wrote: “Divine Providence granted us such a diligent observer in Tycho Brahe, that his observations convicted this Ptolemaic calculation of an error of eight minutes; it is only right that we should accept God’s gift with a grateful mind.… Because those eight minutes could not be ignored, they alone have led to a total reformation of astronomy.”
After eight years of intense effort Kepler was finally led to what is now known as the second of his two laws of planetary motion. The second law states that a radius vector drawn from the sun to a planet sweeps out equal areas in equal times, so that when the planet is close to the sun it moves rapidly and when far away it goes slowly. First correctly stated in book 5 of his Epitome astrononiae Copernicanae (Epitome of Copernican Astronomy), published in 1621, the law worked well for the earth’s orbit, but when it was applied to Mars the 8-minute discrepancy once again appeared, which made Kepler realize that the planetary orbits might not be circular.
Kepler knew that the epicycle theory for Mercury gave an ovoid curve, but when he tried this for Mars the discrepancy was still 4 minutes of arc. Seeing that the ovoid curve he had drawn for the orbit of Mars was quite similar to an ellipse, he began thinking of the possibility that the planetary orbits were elliptical. As he wrote to his friend David Fabricius in July 1603: “I lack only a knowledge of the geometric generation of the oval or face-shaped curve.… If the figure were a perfect ellipse, then Archimedes and Apollonius would be enough.” He soon realized that an ellipse would satisfy the calculations, but such an orbit did not fit in with his idea that the motion of the planets was driven by the magnetic field of the rotating sun. He expresses his frustration in chapter 58 of his Astronomiae nova, published in 1609:
I was almost driven to madness in considering and calculating this matter. I could not find out why the planet would rather go on an elliptical orbit. Oh, ridiculous me! As the libration in the diameter could not also be the way to the ellipse. So this notion brought me up short, that the ellipse exists because of the libration. With reasoning derived from physical principles, agreeing with experience, there is no figure left for the orbit of the planet but a perfect ellipse.
Thus he arrived at what is now known as Kepler’s first law of planetary motion, which is that each of the planets travels in an elliptical orbit, with the sun at one of the two focal points of the ellipse. The second law states that a radius vector drawn from the sun to a planet sweeps out equal areas in equal times. These two laws, which first appeared in Kepler’s Astronomia nova, became the basis for his subsequent work on the Rudolphine Tables.
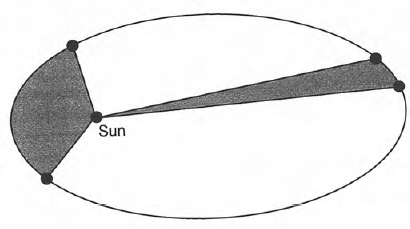
Kepler’s first two laws of planetary motion: (1) each of the planets travels in an elliptical orbit, with the sun at one of the two focal points of the ellipse; (2) a radius vector drawn from the sun to a planet sweeps out equal areas in equal times
Kepler’s first two laws of planetary motion eliminated the need for the epicycles, eccentrics, and deferents that had been used by astronomers from Ptolemy to Copernicus. The passing of this ancient cosmological doctrine was noted by Milton in book 8 of Paradise Lost:
Hereafter, when they come to model Heaven,
And calculate the stars; how they will wield
The mighty frame; how build, unbuild, contrive
To save appearances; how gird the sphere
With centric and eccentric scribbled o’er,
Cycle and epicycle, orb in orb.
Kepler wrote three other works on his research before the publication of his Astronomia nova. The first was Astronomomiae pars optica, published in 1603, and the second was Ad Vitellionem paralipomena (Appendix to Witelo), which came out the following year. Both books dealt with optical phenomena in astronomy, particularly parallax and refraction, as well as the annual variation in the size of the sun.
The third book was occasioned by another new star that appeared in October 1604 in the vicinity of Jupiter, Saturn, and Mars. Kepler published an eight-page tract on the new star in 1606 entitled De stella nova, with a subtitle describing it as “a book full of astronomical, physical, metaphysical, meteorological, astrological discussions, glorious and unusual.” At the end of the tract Kepler speculated on the astrological significance of the new star, saying that it might be a portent of the conversion of the American Indians, a mass migration to the New World, the downfall of Islam, or even the second coming of Christ.
Meanwhile the whole science of astronomy had been profoundly changed by the invention of the telescope. Instruments called “perspective glasses” had been used in England before 1580 for viewing distant terrestrial objects, and both John Dee and Thomas Digges were known to be expert in their construction and use, though there is no evidence that they used them for astronomical observations. But their friend Thomas Harriot is known to have made astronomical observations in the winter of 1609–1610 with a small “telescope,” which may have been a perspective glass.
Other than these perspective glasses, the earliest telescope seems to have appeared in 1604, when a Dutch optician named Zacharias Janssen constructed one from a specimen belonging to an unknown Italian, after which he sold some of them at fairs in northern Europe. When Galileo heard of the telescope he constructed one in his workshop in 1609, after which he offered it to the Doge of Venice for use in war and navigation. After improving on his original design, he began using his telescope to observe the heavens, and in March 1610 he published his discoveries in a little book called Siderius nuncius (The Starry Messenger).
Galileo sent a copy of the Siderius nuncius to Kepler, who received it on April 8, 1610. During the next eleven days Kepler composed his response in a little work called Dissertatio cum Nuncio sidereal (Answer to the Sidereal Messenger), in which he expressed his enthusiastic approval of Galileo’s discoveries and reminded readers of his own work on optical astronomy, as well as speculating on the possibility of inhabitants on the moon and arguing against an infinite universe. Galileo wrote a letter of appreciation to Kepler: “I thank you because you are the first one, and practically the only one, to have complete faith in my assertions.”
Kepler borrowed a telescope from the elector Ernest of Cologne at the end of August 1610, and for the next ten days he used it to observe the heavens, particularly Jupiter and its moons. He published the results the following year in a booklet entitled Narratio de Jovis satellitibus, confirming the authenticity of Galileo’s discovery.
That same year Kepler published a letter entitled Strena, which in its English translation is known as “A New Year’s Gift, or On the Six-Cornered Snowflake,” in which he reflects on the reason why snowflakes are hexagonal. Owen Gingerich described this minor work as “a perceptive, pioneering study of the regular arrangements and the close packing that are fundamental in crystallography.”
Kepler’s excitement over the possibilities of the telescope was such that he spent the late summer and early autumn of 1610 making an exhaustive study of the passage of light through lenses, which he published later that year under the title Dioptrice, which became one of the foundation stones of the new science of optics.
The death of Rudolph II early 1612 forced Kepler to leave Prague and take up the post of district mathematician at Linz, where he remained for the next fourteen years. One of his official duties was a study of chronology, part of a program of calendar reform instituted by the archduke Ferdinand II, son of the late emperor Rudolph. As a result of his studies he established that Christ was born in what in the modern calendar would be 5 BC.
During the period that Kepler lived in Linz, he continued his calculations on the Rudolphine Tables and published two other major works, the first of which was De harmonice mundi (The Harmony of the World), which appeared in 1619. The title was inspired by a Greek manuscript of Ptolemy’s treatise on musical theory, the Harmonica, which Kepler acquired in 1607 and used in his analysis of music, geometry, astronomy, and astrology. The most important part of the Harmonice is the relationship now known as Kepler’s third law of planetary motion, which he discovered on May 15, 1618, and presents in book 5. The law states that for each of the planets the square of the period of its orbital motion is proportional to the cube of its average distance from the sun.
There had been speculations about the relation between the periods of planetary orbits and their radii since the time of Pythagoras, and Kepler was terribly excited that, following in the footsteps of Ptolemy, he had at last found the mathematical law “necessary for the contemplation of celestial harmonies.” He wrote of his pleasure “that the same thought about the harmonic formulation had turned up in the minds of two men (though lying so far apart in time) who had devoted themselves entirely to contemplating nature.… I feel carried away and possessed by an unutterable rapture over the divine spectacle of the heavenly harmony.”
Kepler dedicated the Harmonice to James I of England. The king responded by sending his ambassador, Sir Henry Wooton, with an invitation for Kepler to take up residence in England. But after considering the offer for a while, Kepler decided against it.
The English poet John Donne was familiar with the work of Copernicus and Kepler, probably through Thomas Harriot. Donne had in 1611 said to the Copernicans that “those opinions of yours may very well be true … creeping into every man’s mind.” That same year Donne lamented the passing of the old cosmology in “An Anatomy of the World”:
And new Philosophy calls all in doubt,
The Element of fire is quite put out;
The Sun is lost, and th’earth, and no man’s wit
Can well direct him, where to look for it.
Kepler’s second major work at Linz was his Epitome astronomiae Copernicanae (Epitome of Copernican Astronomy), published in 1621. In the first three of the seven books of the Epitome Kepler refutes the traditional arguments against the motions of the earth, going much farther than Copernicus and using principles that Galileo would later give in greater detail. His three laws of planetary motion are explained in great detail in book 4, along with his lunar theory. The last three books treat practical problems involving his first two laws of planetary motion as well as his theories of lunar and solar motion and the precession of the equinoxes. The work became very popular, and, according to J. L. Russell, “from 1630 to 1650 the Epitome was the most widely read treatise on theoretical astronomy in Europe.”
In 1626 Kepler was forced to leave Linz and move to Ulm, from where he moved on to Sagan in 1628, then two years later he traveled to Regensburg, where he died of an acute fever on November 15, 1630. His tombstone, now lost, was engraved with an epitaph that he had written himself: “I used to measure the heavens, now I measure the shadow of the earth. / Although my soul was from heaven, the shadow of my body lies here.”
While Kepler was still in Ulm he published the Rudolphine Tables in September 1627, dedicating them to the archduke Ferdinand II. A decade earlier Kepler had come across the pioneering work on logarithms published in 1614 by the Scottish mathematician John Napier (1550–1617). He used logarithms in computing the planetary positions in the Rudolphine Tables, appending logarithmic tables as well as a catalogue of the celestial coordinates of a thousand stars, all based on the Copernican theory. The new tables were far more accurate than any in the past, and they remained in use for more than a century.
Kepler used his tables to predict that Mercury and Venus would make transits across the disk of the sun in 1631. The transit of Venus was not observed in Europe because it took place at night. The transit of Mercury was observed by Pierre Gassendi in Paris on November 7, 1631, representing a triumph for Kepler’s astronomy, for his prediction was in error by only 10 minutes of arc as compared to 5° for tables based on Ptolemy’s model.
Kepler’s last work, published posthumously in 1634, was a curious tract called Somnium seu astronomia lunari (Dream on Lunar Astronomy), which has been described as the first work of science fiction. It tells of how a student of Tycho Brahe is transported by occult forces to the moon, from where he describes the earth and its motion around the sun along with the other planets.
Kepler’s three laws of planetary motion were to become the basis of the new heliocentric astronomy that emerged in the seventeenth century, culminating in Newton’s Principia, published in 1687. When the Principia was first introduced to the Royal Society in London, it was described as “a mathematical demonstration of the Copernican hypothesis as proposed by Kepler.” The astronomer Edmond Halley, in his review, wrote that Newton’s first eleven propositions in book 1 of the Principia were “found to agree with the Phenomena of the Celestial Motions, as discovered by the great Sagacity and Diligence of Kepler.”