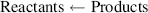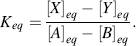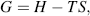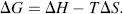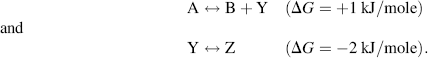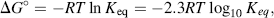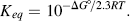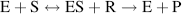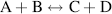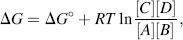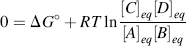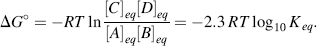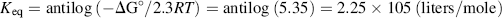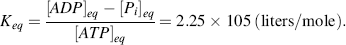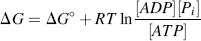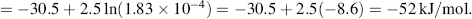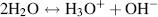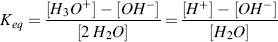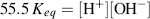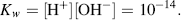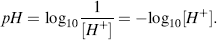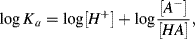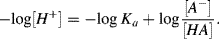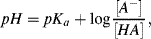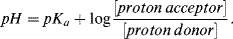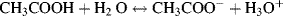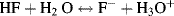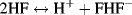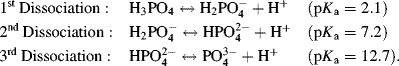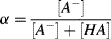Chapter 1

Basic Chemical and Biochemical Concepts

1.1 Chapter Overview

This chapter presents the background concepts of chemistry and thermodynamics of relevance to the subject of bioelectronics, and which are discussed further in most chapters of this book. The level of the material covered in this chapter is probably comparable to that covered by most students in pre-university basic chemistry courses. Graduates in engineering and the physical sciences may need to dig deeply into their recollections of such courses, and may also face new concepts. One objective here is to provide an awareness of some basic concepts of the chemical and energetic functioning of biological systems, of which even a modest understanding will go a long way to mastering the interdisciplinary field of bioelectronics.

After reading this chapter readers will gain a refreshed or new understanding of:

i. the formation of chemical bonds and how biological systems make use of the change in Gibbs free-energy ΔG of chemical reactions to perform the work required to retain their biological viability;

ii. chemical concentrations and activity coefficients;

iii. the concepts of nonpolar, polar, ionic, and hydrogen bonds;

iv. acids, bases and the biological importance of pH and buffers.

1.2 Energy and Chemical Reactions

1.2.1 Energy

A distinguishing characteristic of a living, rather than a nonliving, system is the ability to perform chemical transformations that produce fluxes of matter and energy. This process describes metabolism. Other characteristics that aid the identification of the living state are molecular organisation into systems of increasing complexity, and the abilities to self-produce and adapt to changes in environmental factors. The minimal level of organisation capable of exhibiting all these characteristics is the cell. The two principal forms of energy are kinetic and potential, associated with motion and stored energy, respectively. Kinetic energy in a molecular system can be interpreted in terms of the motions of its constituent molecules, which we term as heat. This heat can be determined indirectly by measuring the temperature of the molecular system. For heat to perform work (such as by an engine) it must flow from a region of higher to lower temperature. However, living systems are isothermal – they function at constant temperature and cannot utilise heat flow as a source of energy. Instead, living systems utilise the potential energy stored in the chemical bonds of molecules such as glucose or adenosine triphosphate (ATP). Cells continuously degrade such molecules, and the potential energy released when their chemical bonds are broken is used to perform various kinds of work, including the pumping of substances across membranes to produce chemical concentration gradients that in turn serve as sources of stored potential energy. This process, where chemical bond energy is converted into energy stored in the form of a chemical concentration gradient, is an example of the first law of thermodynamics which states that energy can neither be created nor destroyed. Other biological examples of this law include photosynthesis where the energy of sunlight absorbed by green leaves is converted into the chemical bond energy of glucose molecules, and in the conversion of chemical bond energy into mechanical and electrical energy by muscle cells and nerve cells, respectively.

All of the metabolic processes that produce the energy fluxes required for maintaining the living state involve the making and breaking of strong, covalent, chemical bonds between atoms in a molecule.

1.2.2 Covalent Chemical Bonds

Most biological molecules contain only six different atoms, namely carbon, hydrogen, oxygen, nitrogen, phosphorus and sulphur. The locations of these atoms in the Periodic Table of Elements are shown in Table 1.1. The electron shells of the atoms are labelled K, L and M. Each shell is composed of one or more subshells that represent the electronic orbitals about the nucleus of the atom. The first shell, K, has one subshell called the 1s shell and can accommodate a maximum of two electrons. The second shell, L, has two subshells (2s, 2p) that can accommodate a maximum of eight electrons, with six in the 2p shell. The third shell, M, has three subshells (3s, 3p, 3d) and can accommodate a maximum of 18 electrons, with 10 in the 3d shell.

Table 1.1 The locations of hydrogen (H), carbon (C), nitrogen (N), oxygen (O), phosphorus (P) and sulphur (S) in the Periodic Table of Elements.

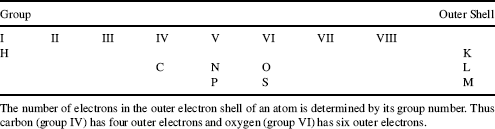
Electrons in the outer shells have higher average energies than those in the inner shells, and their electron orbitals can extend farther from the nucleus. This contributes to how chemically reactive a particular atom may be in its interaction with other atoms. We can schematically represent the number and arrangement of electrons in the outer electron shells of these atoms as follows [1, 2]:

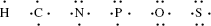
A covalent bond is formed by the sharing of unpaired electrons, one from the outer electron shell of each atom, between the nuclei of two atoms. These shared electrons then enter an electronic orbital that is common to both atoms, acting to reduce the repulsive force between the two positively charged nuclei and to hold them closely together. Thus, the hydrogen atom with one unpaired electron can form only one covalent bond, whilst carbon with four electrons forms four bonds. An example of this is methane (CH₄):

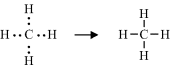
In the methane molecule the carbon atom is covalently bonded to four hydrogens.

In ethylene (C₂H₄) the two carbon atoms are held together by a double bond, and through the polymerisation of ethylene these double bonds are opened up to form the structure of polyethylene:

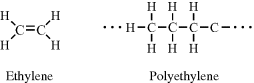
The nitrogen and phosphorus atoms possess five electrons in their outer electronic shells. These atoms can form either three covalent bonds (leaving a lone pair of unbonded electrons) or five covalent bonds. Examples include ammonia (NH₃) and phosphoric acid (H₃PO₄):

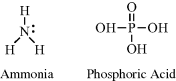
Oxygen contains six electrons in its outer electronic shell (known as the p-shell) and requires just two more electrons to completely fill this shell. It can accomplish this by forming two covalent bonds with another atom, such as in molecular oxygen (O₂) or in the carbonyl (C=O) chemical group:

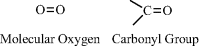
The sulphur atom can also form two covalent bonds in this manner, as in hydrogen sulfide (H₂S). The outer electronic shell of the oxygen atom has two pairs of electrons that are not involved in covalent bond formation. This, however, does not apply to the sulphur atom, which can form as many as six covalent bonds as in sulphuric acid (H₂SO₄):

1.2.3 Chemical Concentrations

Concentrations of substances dissolved in solutions are often given in terms of weight/volume (e.g. mg/L, or mg/100 mL – a common clinical unit). These units do not depend on knowledge of the molecular structure of the measured substance. For a substance with a known molecular structure, one can define a mole of that substance.

Moles and Avogadro's Number: A mole (symbol mol) of substance contains as many objects (e.g. atoms, molecules, chemical formula units) as there are atoms in exactly 12 gm of carbon-12. (There are three naturally occurring isotopes of carbon, namely carbon-12, -13 and -14 (

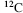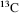, and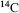

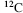is the most abundant and is used as the standard from which atomic masses of all nuclides are measured. The atomic mass of

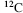is by definition 12. The radioactive isotope

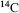is formed at a constant rate in a chain reaction initiated by cosmic ray protons blasting nuclei in the upper atmosphere to produce neutrons, which in turn bombard nitrogen atoms to form

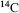which then combines with oxygen to form carbon dioxide.) The number of atoms in 12 gm of

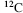is equivalent to Avogadro's Number, of value 6.022 × 10²³, and by convention is given the dimension mol⁻¹. Thus, 1 mol of water molecules contains 6.022 × 10²³ water molecules, and 1 mol of E. coli comprises 6.022 × 10²³ of these microorganisms.

Molar Mass: From the above definition it follows that a mole of any pure substance has mass (in grams) exactly equal to that substance's molecular or atomic mass (in atomic mass units). Molar mass is expressed in units of g/mol. The Dalton (symbol Da) is often employed by biochemists as the unit of molar mass, and is defined as 1 Da = 1 g/mol. Simple chemical compounds have molar masses typically in the range 10–1000 g/mol, and for biopolymers such as proteins and nucleic acids values ranging from 1000 to 5 × 10⁶ are common. The atomic mass values for the most common atoms of biological interest are shown Table 1.2.

From Table 1.2 we can deduce that the molar mass of hydrogen gas (H₂) is just over 2 g/mol, and that pure magnesium has a molar mass of 24.31 g/mol. Alternatively, we can say that 1 mol of hydrogen gas is equivalent to 2.016 gm of hydrogen gas, and that 1 mol of pure magnesium is equivalent to 24.31 grams of pure magnesium. Likewise, 58.44 grams of anhydrous (dry) NaCl represents 1 mol of sodium chloride, and 95.21 grams of anhydrous MgCl₂ represents 1 mol of magnesium chloride.

Molar Solution: This is an aqueous solution consisting of one mole of a substance plus enough water to make one litre of solution. Another measure of concentration that we can use is a Molal Solution, which is an aqueous solution consisting of one mole of a substance plus 1 kg of water (usually very close to 1 L water). The total volume may thus be more than 1 L. The difference between molar and molal is important for solutions containing a large amount of nonaqueous substance. For example, cream has 20% fat that is homogenised in very small droplets. There will be a 20% difference between the molarity and molality of its salt content, because all the salt will be dissolved in the 80% that is water. Thus, if the actual concentration (molality) of the sodium content is 24 mMolal (moles/L water), this could be reported on the product's label as being 20 mMolar (moles/L cream), which for consumers concerned about their daily salt intake can (mistakenly) appear more acceptable.

Concentrations of ions are often given in Equivalents (or milliequivalents, mEq) per Litre. The equivalents of an ion are equal to the molarity times the number of charges per molecule. For example, a solvated sodium ion has a single charge, whereas calcium and magnesium ions have two charges. (From Table 1.2 we can see that Ca and Mg are group II atoms, and thus each has two outer valence electrons that are readily donated to two chloride atoms in the formation of calcium chloride and magnesium chloride salts, for example.) Thus, the concept of Equivalents is the measure of Charge concentration.

Since the molarity of a solution describes the number of individual particles dispersed in a given volume of solution, the concept for electrolytes such as sodium chloride is more complicated than for nonelectrolytes because of ionic dissociation. For example, 1 mol of NaCl dissolved in water produces nearly twice as many particles as a mole-equivalent weight of glucose, since the salt dissociates into Na⁺ and Cl⁻ whereas glucose retains its single molecule character. Because of electrostatic interaction between the positive ions (cations) and negative ions (anions) there is a statistical probability that at any instant some Na⁺ will be associated with Cl⁻. The electrolyte therefore behaves as if it were not 100% dissociated. Because the electrostatic force between ions decreases with the square of the distance between them, the electrolyte will effectively become more dissociated if the solution is more dilute. Thus, the activity (i.e. effective free concentration) of an ion depends on its tendency to dissociate in solution, as well as on its total concentration.

Some activity coefficients (defined as the ratio of the activity divided by the molal concentration) as a function of concentration at 25 °C are given in Table 1.3.

Table 1.2 Part of the simplified Periodic Table of Elements to give the mass, in atomic mass units (amu), of some atoms of biological importance.

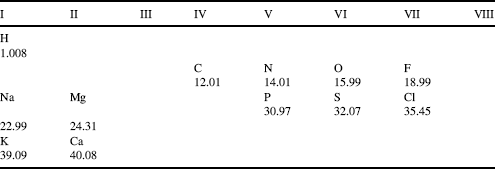
Table 1.3 Activity coefficient values for some common compounds that dissociate into ions in solution. (Derived from the CRC Handbook of Chemistry and Physics, 87th edn, 2006–2007).

1.2.4 Nonpolar, Polar and Ionic Bonds

In a covalent bond formed between two identical atoms, such as the CߝC bond, the bonding electrons are equally shared between the atoms. Such a bond is termed nonpolar. Molecules such as Cl₂, H₂ and F₂ are nonpolar, for example. In the description of the concentrations of ions in terms of their equivalents of charge concentration, we have alluded to the concept that different atoms exhibit different tendencies for the sharing of electrons. This tendency can be quantified by their electronegativity, using a scale measured from a hypothetical zero to a maximum value of 4.0 (close to that possessed by the most electronegative atom, fluorine). The electronegativity values of some atoms are listed in Table 1.4.

Table 1.4 The electronegativity values for the atoms listed in Table 1.2 based on the Pauling electronegativity scale [4].

We note from Table 1.4 that atoms toward the upper right of the Periodic Table of Elements are more electronegative, and those to the lower left are least electronegative. From this table we can judge that carbon disulphide (CS₂) has almost equal sharing of its electrons when forming its CߝS covalent bonds, and so has nonpolar bonds. As a guideline, a maximum difference of 0.4 ~ 0.5 in electronegativity is often used to define the limit for the formation of a nonpolar bond. For the CߝCl bond there is an unequal sharing of electrons, with electronic charge on average spending more time nearest to the chlorine atom (giving it a slightly negative charge δ−) and less time near to the carbon atom (making it slightly positively charged δ+). We say that this bond is a polar bond. The HߝF bond is particularly polar. Molecules such as NH₃ and H₂O also possess polar bonds, and this lends to them the properties of an electric dipole moment (Figure 3.2, Chapter 3). They will tend to align themselves with an externally applied electric field. Typically, chemical bonds formed between atoms having an electronegativity difference less than 1.6 (but greater than 0.5) are considered to be polar. For larger differences we approach the situation where there is complete transfer of an electron from the least to the most electronegative atom. This type of bond is termed ionic. The guideline here is that when the electronegativity difference is greater than 2.0 the bond is considered to be ionic. Common salt (NaCl) is a good example, forming ionic crystals held together by the coulombic forces between the positively charged Na⁺ and negatively charged Cl⁻ atoms. KCl and MgCl₂ are other examples of an ionic solid.

If two highly electronegative atoms are bonded together, the bond between them is usually quite unstable. This occurs in hydrogen peroxide (HߝOߝOߝH), where the strong attractions of bonding electrons towards the two strongly electronegative oxygen atoms make it a highly reactive molecule.

1.2.5 Van der Waals Attractions

Atoms can be defined by a characteristic ‘size’ known as their van der Waals radius. This radius can be determined from investigations of the mechanical properties of gases, from X-ray determinations of the atomic spacing between unbonded atoms in crystals, and from dielectric and optical experiments. The van der Waals radii for some atoms of biological relevance are given in Table 1.5.

Table 1.5 Van der Waals radii values for some atoms (derived from [5]).

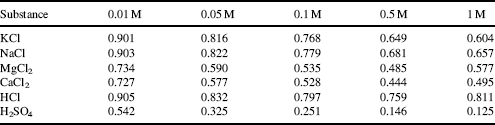
If two nonbonding atoms are brought together they initially show a weak bonding interaction, produced by fluctuating electric interactions of the outer electrons of one atom with the positive charge of the other atom's nucleus, and vice versa. As depicted in Figure 1.1 this can be considered as a fluctuating dipole–dipole interaction between the atoms.

Figure 1.1 Van der Waals attractive interactions arise from dipole-dipole interactions between two nonbonding atoms. This interaction fluctuates in tune with how the outer electrons in each atom distribute themselves in their orbitals. In a covalent bond, where a pair of electrons occupies a common (molecular) orbital, the atoms are brought closer together than the sum of their van der Waals radii.

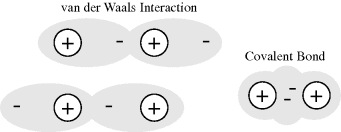
The attraction force between the two atoms increases until their separation distance begins to get less than twice the sum of their van der Waals radii, at which point the two atoms repel each other very strongly. A mathematically simple model, known as the Lennard-Jones 6–12 potential, can be used to approximate the interaction between a pair of electrically neutral atoms or molecules [3]. The attractive long-range interaction varies as 1/r⁶, where r is the interatomic distance, and the short-range repulsive force is assumed to vary as 1/r¹². The resultant energy is taken as the sum of these two terms and, as shown in Figure 1.2, the equilibrium distance between the two atoms or molecule corresponds to the minimum of the potential energy curve. An insight into the origins of the 1/r⁶ and 1/r¹² dependencies is given in Chapter 3. This model is often used to describe the properties of gases and to model the interatomic interactions in molecular models.

Figure 1.2 The resultant van der Waals force (solid line) can be approximated as the sum of the long-range attractive interaction, assumed to vary as r⁻⁶, and the short-range repulsive force which varies as r⁻¹² [3]. The equilibrium distance, in radii units r, is located at the minimum of the resulting potential energy (PE) curve.

Van der Waals attraction between two atoms is weak, but when many atoms are involved, as occurs for two macromolecular ‘surfaces’ coming into intimate contact, it can become a significant force of attraction. For example, van der Waals interactions make an important contribution to the total force holding together the stable conformations of large molecules such as proteins. When two atoms form a covalent bond, their atomic centers are much closer together than the sum of their van der Waals radii. For example, a single-bonded carbon pair is separated by 0.15 nm, and double-bonded carbons are 0.13 nm apart.

1.2.6 Chemical Reactions

Chemical reactions involve the breaking and forming of covalent bonds, which in turn entails the flow of electrons. When writing down the course of a chemical reaction, curved arrows (known as ‘electron pushing arrows’) are used to symbolise the electron flow. An example is shown below for the reaction between ammonia and formaldehyde, and is a step in the eventual production of hexamine:

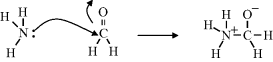
In the reaction shown above, one of the lone pair of electrons on the nitrogen atom of the ammonia molecule is donated to form a covalent bond with the carbon atom of formaldehyde. This leaves a positive charge on the nitrogen atom. To maintain the situation that carbon forms four covalent bonds, the double bond is broken down to just a single bond. One of the two electrons so released is used to create the NߝC bond, whilst the other is donated to the oxygen atom (leaving it negatively charged).

In accordance with the first law of thermodynamics, the amount of energy released on the formation of a covalent bond is equal to that required for the breaking of it. The strengths of some chemical bonds, in terms of the amount of energy required to break the bond, are given in Table 1.6.

Table 1.6 The strengths of some chemical bonds [6].

To interpret the concept of chemical bond strength, let us consider the CߝC bond. From Table 1.6 we note that one mole of CߝC bonds has a bond energy of 346 kJ. The energy required to break a single CߝC bond is thus 3.46 × 10⁵ J/(6.022 × 10²³ bonds/mol) = 5.75 × 10⁻¹⁹ J. To break the CߝC bond let us assume we need to ‘stretch’ it by 0.2 nm, so that the carbon atoms are spaced 0.35 nm apart, a distance of just over twice the sum of their van der Waals radii. Energy E is expended when a force F moves an object through a distance d (E = F.d). The force required to break a CߝC bond can thus be estimated as the bond energy 5.75 × 10⁻¹⁹ J divided by the stretch distance 0.2 nm = 2.87 nN (1 Joule = 1 Newton.meter). To help place this into perspective we can use the concept of tensile strength, which is the force required (per unit area) to break a material. If we think of a CߝC bond as a carbon wire, it will have a cross-sectional area of ~2 × 10⁻²⁰ m². The tensile strength of a CߝC bond is thus ~2.87 nN/(2 × 10⁻²⁰ m²) ≈ 1.44 × 10¹¹ N/m² = 144 GPa (1 Pascal (Pa) = 1 N/m²). By comparison, the tensile strength of materials such as stainless steel and titanium are less than 1 GPa.

Performing a bookkeeping exercise on the number and type of covalent bonds involved in the reaction we have depicted for ammonia and formaldehyde, we see that the C=O bond is replaced with a CߝO bond, and that a CߝN bond is created. From Table 1.6 we can deduce that if 1 mole of ammonia is reacted with 1 mole of formaldehyde to produce 1 mole of the intermediary product, there is a total bond energy loss of 67 kJ. This loss of bond energy will be given off as heat during the reaction. However, in practice, the amount of heat generated will depend on how much of the original reactants convert into the product. In other words, we need to know the equilibrium state of the reaction.

All chemical reactions reach an equilibrium state. When the reactants are first brought together they react at a rate determined by their initial concentrations. This follows from the Law of Mass Action, which states that the rate of a chemical reaction is proportional to the active masses of the reacting substances. We can represent a reaction as:

The concentrations of the reactants decrease as the reaction progresses and their rate of reaction decreases. At the same time, as the amounts of products accumulate they begin to participate in the reverse reaction:

Finally, the stage will be reached where the rates of the forward and reverse reactions become equal and the concentrations of the reactants and products do not change with time. We say that the reaction has reached chemical equilibrium. The equilibrium constant for the reaction is defined as the ratio of the equilibrium concentrations of the products and reactants. For a simple reaction A + B ↔ X + Y

(1.1) equation

The custom is to use square brackets to designate the equilibrium molar concentrations under standard conditions, namely at 25 °C (298 K) and at a pressure of 1 atmosphere. By convention, when water (H₂O) or hydrogen ions (H⁺) are reactants or products, they are treated in Equation (1.1) as having effective concentrations (activities) of unity (see also Section 1.3). Thus, under standard conditions and starting with 1 M concentrations for all the components of the reaction, when K_eq > 1.0 the reaction proceeds in the forward direction (A + B → X + Y), whilst for K_eq < 1.0 the reactions proceeds in reverse (A + B ← X + Y).

1.2.7 Free-Energy Change ΔG Associated with Chemical Reactions

Because biological systems function at constant temperature and pressure, we can use as a measure of the potential energy released or stored in chemical reactions the concept of Gibbs free-energy (named after Josiah Willard Gibbs, an early founder of the science of thermodynamics). Gibbs demonstrated that free-energy G is given by the relationship:

where H is the heat energy (also termed enthalpy) of the chemical system, T is the absolute temperature, and S is termed the entropy and provides a measure of the degree of disorder of the system. We are interested in the change of free-energy ΔG that results from a molecule's chemical structure being changed in a chemical reaction. Contributions to the ΔG of a reaction, at constant temperature and pressure, come from the change in heat content between reactants and products, and the change in entropy of the system:

Enthalpy H is released or absorbed in a chemical reaction when bonds are formed or broken. ΔH is thus equal to the overall change in bond energies. We can distinguish between a reaction in which heat is given off (an exothermic reaction) and one in which heat is absorbed (an endothermic reaction). In an exothermic reaction ΔH is negative and the products contain less energy than the original reactants. This is the situation we have deduced for the initial reaction of ammonia with formaldehyde. In an endothermic reaction (heat absorbed) ΔH is positive and the products contain more energy than the reactants.

By convention, ΔS is positive when entropy, and thus disorder, increases. The second law of thermodynamics states that the entropy of an isolated system, which is not in equilibrium, will tend to increase over time and to approach a maximum value at equilibrium. The change in Gibbs free-energy ΔG for a spontaneous chemical reaction is always negative, and so a negative value for ΔH (heat given off) and a positive ΔS tend to lead to a spontaneous reaction. Under certain conditions a chemical reaction having a positive ΔG can also occur spontaneously. For this to occur it must be strongly coupled with another reaction having a negative ΔG of larger absolute value than the nonspontaneous reaction. For example, suppose we have the following two reactions:

Formation of B + Y in the first reaction will not occur spontaneously, but any Y that is formed is converted spontaneously to Z in the second reaction. This lowers the equilibrium concentration of Y in the first reaction and has the effect of pushing the reaction to produce more B + Y. The way this feeds into the sum of the two components of the overall reaction A ↔ B + Z having a negative ΔG can be represented by:

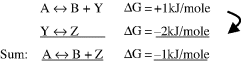
Energetically unfavourable reactions of the type A ↔ B + Y are common in cells and are often coupled to reactions having a large negative ΔG. We will see that an important example of this is the coupling of reactions to the hydrolysis of the molecule adenosine triphosphate (ATP).

The concept of heat being generated or absorbed during a chemical reaction is straightforward – but how do we judge whether there is an increase or decrease in entropy? Determining whether a chemical reaction produces more molecules as products than were originally present in the reactants can provide a simple guide. If the reaction produces an increased number of molecules of the same physical state (i.e. solid, liquid or gas) there will be an increase of entropy, because their constituent atoms will be more randomly dispersed and thus more disordered. Likewise, if a solid reactant converts into either a liquid or gas, its constituent atoms will gain dynamic freedom and thus an increase of entropy.

Chemists define a standard set of conditions to describe the standard free-energy change ΔG° of a chemical reaction. The reaction is assumed to occur at 298 K (25 °C) for gases at 1 atmosphere (101.3 kPa) and solute concentrations of 1 M. It can be shown that the relationship between the equilibrium constant K_eq and the standard free-energy change ΔG° is given by the expression

(1.2) equation

where R is the gas constant (8.314 J mol⁻¹ K⁻¹) and T is the standard temperature (298 K). Thus, K_eq values of 10 and 0.1 litres/mol, for example, correspond to ΔG° values of −5.7 kJ/mol and +5.7 kJ/mol, respectively. Equation (1.2) can also be written in the form:

When a chemical reaction is not at equilibrium we can interpret the free-energy change for the reaction, ΔG°, as the driving force that tends to drive the reaction towards equilibrium. In this way, we can view ΔG° as an alternative description of the equilibrium constant K_eq of a chemical reaction. We should note, however, that this tells us nothing about the rate of a chemical reaction. Many chemical reactions that have a large negative ΔG° value may not proceed at a measurable rate at all! We have seen that chemical reactions involve the breaking and making of covalent bonds. This can only occur if the reacting molecules come close enough together during a collision between them. Some of these collisions may provide the opportunity for the desired sharing of valence electrons between an atom and its ‘target’ reactant, but many other collisions may not. An effective way to increase the rate of a chemical reaction is to add a nonreacting compound, called a catalyst, that facilitates the breaking and making of new bonds between the reactants. Catalysts commonly perform this helpful task by causing a redistribution of the electrons in the reacting atoms, such that the bonds that need to be broken are weakened. This lowers the energy barrier in the reaction ‘pathway’ and increases the reaction rate. After the reaction occurs, the catalyst becomes available to repeat this procedure with another set of reactants. In this way, the catalyst is not consumed in the reaction. The catalysts that take part in biological reactants are large protein molecules called enzymes. As depicted in Figure 1.3 an enzyme catalysed reaction involves the reacting molecule (the substrate) ‘locking’ neatly into an enzyme's receptor site that is specifically configured for that specific substrate.

Figure 1.3 In an enzyme catalysed reaction the reactant (substrate S) first binds to a specific site on the enzyme to form an enzyme-substrate complex E-S. The bound substrate then reacts with another reactant to form a product P, leaving the enzyme E available for further reactions.

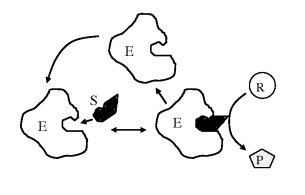
The overall reaction shown in Figure 1.3 can be written as:

We should also be aware that the standard Gibbs free-energy change ΔG° informs us how far, and in which direction, a reaction will go to reach equilibrium only when the starting concentration of each chemical component is 1 M and at the standard conditions for temperature (298 K) and pressure (101.3 kPa). However, for practically all cases we are only really interested in the actual free-energy change ΔG for reactions where the chemical concentrations are not all the same and not equal to 1 M, and for temperatures other than 298 K. It can be shown for any chemical reaction

that ΔG and ΔG° are related by the expression:

(1.3) equation

where the concentrations of the various components and the temperature T are those actually involved. When the reaction reaches the equilibrium state, at which point there is no driving force for the reaction and ΔG = 0, Equation (1.3) reduces to (1.2):

For almost all types of biological organism, the most important source of free-energy is generated by the breaking of a phosphate bond in adenosine triphosphate (ATP). ATP consists of adenosine (composed of an adenine group and a ribose sugar) and three phosphate groups (triphosphate), two of which are often referred to as ‘high-energy bonds’. One or both of these bonds can be broken by an enzyme-catalysed hydrolysis reaction. Hydrolysis is a reaction in which a molecule is cleaved into two parts by the addition of a water molecule. The case where one bond is broken, to form adenosine diphosphate (ADP) plus inorganic phosphate (P_i) and a proton (H⁺), is depicted below:

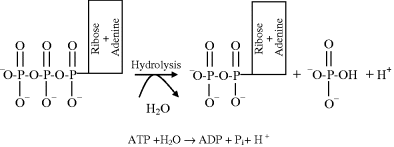
The standard Gibbs free-energy change ΔG° for this reaction is −30.5 kJ/mol, which from Equation (1.2) corresponds to an equilibrium constant:

From Equation (1.1) and noting we can by convention treat the water and hydrogen ion components as having activities equal to 1.0, the equilibrium concentrations of ATP, ADP and P_i satisfy the relationship:

However, this does not reflect the actual concentrations found in living cells. For example in the cytoplasm of a red blood cell the concentrations of ATP and ADP are typically 2.25 and 0.25 mM, respectively, and inorganic phosphorus P_i has a concentration of 1.65 mM. This gives [ADP][P_i]/[ATP] = 1.83 × 10⁻⁴, a value some nine orders of magnitude away from the equilibrium situation! The hydrolysis of ATP to ADP is being driven very hard, and this means that the free-energy change available to do useful work is high. We can calculate this free-energy change from Equation (1.3). Assuming a normal physiological temperature of 37 °C (310 K) we have:

Thus, the free-energy released by the conversion of ATP into ADP within a cell is significantly larger than the standard free-energy change. Cells use this free-energy to perform many functions, such as: the synthesis of important molecules (DNA, RNA, proteins, lipids); the pumping across membranes of ions and molecules against their concentration gradients (see Figure 3.11 and discussion in Chapter 3); in the actions of muscle and nerve cells and the firing of neurons, and to maintain a constant body temperature. In plant cells the energy required to convert ADP back into ATP is supplied by trapping the energy of sunlight through photosynthesis. In animal cells and nonphotosynthetic microorganisms it is supplied by the free-energy released in the enzyme-controlled breaking down of the chemical bonds in glucose molecules.

We noted at the beginning of this chapter that a distinguishing characteristic of a living system is its molecular organisation. In a procedure repeated countless times in cell biology laboratories around the world each day a single microorganism, such as E. coli, can be isolated from an existing culture and transferred to a new culture dish and placed in an incubator. Apart from this single organism, the dish will typically contain no more than magnesium, sulphate, phosphorus and ammonium ions, water and glucose molecules. Within a day or so, depending on the type of organism, a billion or so new cells will have been generated from the original one. For the case of E. coli (a bacterium of cylindrical form about 2 μm long and 1 μm in diameter) its composition includes more than 2 million protein molecules of at least 2000 types, more than 20 million lipid molecules, hundreds of thousands of RNA molecules, and one very large molecule of DNA containing 5 million base pairs. Contained within the volume bounded by its rigid cell wall, formed of interwoven polysaccharides, peptides and lipids, there are also around 300 million ions and metabolites, and some 4 × 10¹⁰ water molecules. Thus, the few types of atoms randomly distributed (i.e. of high entropy) in the culture dish have been incorporated into highly organised (low entropy) systems using the free-energy derived from glucose, in an apparently defiant stance against the finality dictated by the second law of thermodynamics! This apparent contradiction of a basic natural law, that all real processes involve the degradation of energy and the dissipation of order, has been clarified by Schrödinger [7], who explained that living organisms extract ‘negentropy’ from their surroundings. What we call the living-state, a state far removed from equilibrium, is maintained by utilising sources of free-energy provided by the continuous flow of energy from the sun to its end point of wasted heat.

1.3 Water and Hydrogen Bonds

We have noted that the E. coli bacterium contains around 50 billion water molecules – representing about 90% of its total weight. Water also contributes about 70 ~ 80% of the total weight of animal cells. Most of the biochemical reactions taking part in a cell do so in an aqueous environment. Water is the mater and matrix of life. It is the only inorganic liquid that occurs naturally on earth. It is also the only chemical compound that occurs naturally in all three physical states, namely solid, liquid and vapour. According to its molecular size the melting and boiling points of water should be about 100 K lower, and its heat of vaporisation, heat of fusion, and surface tension is higher than that of the comparable hydrides, hydrogen sulphide (H₂S) and ammonia (NH₃) or even than that of most other common liquids. These unique macroscopic properties can only arise from there being strong forces of attraction between the molecules in liquid water – without them water on earth would exist as a gas rather than as a liquid. These strong forces of attraction take the form of hydrogen bonds.

1.3.1 Hydrogen Bonds

A hydrogen atom normally forms just one covalent bond at a time with another atom. However, in Section 1.2.4 we learnt that the water molecule is dipolar. Each hydrogen atom loses a fraction of charge δ− to the oxygen atom, making the oxygen slightly positively charged by an amount 2δ+ to form an electric dipole m, which can align with an externally applied electric field E:

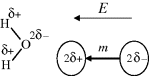
Liquid water is thus a dielectric material possessing a relatively large value of its relative permittivity (dielectric constant) of around 80 at room temperature. The large relative permittivity value for liquid water arises because each water molecule forms transient hydrogen bonds with several other water molecules. The motion of one water molecule dipole moment induced by the electric field is cooperatively coupled to several other water molecules. This cooperative motion enhances the dielectric polarisability of bulk water, because the effective dipole moment per unit volume is larger than that for the situation where each dipole m acted on its own. This makes water a very good solvent for ionic substances (salts) held together by the coulombic force of attraction of the opposite charges of their constituent ions. This force of attraction is inversely proportional to the relative permittivity of the medium in which the ions are embedded. A sodium chloride crystal has a bulk relative permittivity of ~6, and if it is placed in water the force of attraction between the Na⁺ and Cl⁻ ions will be greatly weakened. The crystal will dissociate (dissolve) and the Na⁺ and Cl⁻ ions will be dispersed as free ions in the water. The large electric fields that exist around bare ions such as Na⁺ and Cl⁻ attract water dipoles, which form strongly held hydration sheaths around the ions. Nonionic substances that possess polar chemical bonds are soluble in water. Sugars, alcohol molecules and many other organic molecules readily dissolve in water because they can form hydrogen bonds with water. Nonionic organic molecules, such as benzene or lipids, that are nonpolar are unable to interact with water in this way, and so are insoluble in water.

Hydrogen bonds form because in liquid water a negatively charged oxygen atom can attract a positively charged hydrogen atom, in a neighbouring water molecule, towards one of its unbonded valence electron pairs. This forms a weak bond of strength around 20 kJ/mol (~5 kcal/mol), which is much weaker than the covalent bond between hydrogen and oxygen (~460 kJ/mol). The transient nature of hydrogen bonding between molecules of water can be depicted as shown below:

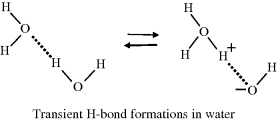
This diagram shows how the covalent and hydrogen bonds may exchange places from one instant to the next. There is thus a finite (but small) probability that the three hydrogen atoms will associate with one oxygen atom to form a hydronium ion (H₃O⁺) leaving another oxygen atom with only one hydrogen to form a hydroxyl ion (OH⁻). The dissociation (ionisation) of water can therefore be written as:

The dissociation of water is sometimes written as H₂O ↔ H⁺ + OH⁻ to emphasise the production of protons. The positively charged hydrogen atoms (protons) of the hydronium ion attract the electronegative, oxygen, ends of the surrounding water molecules to form a stable hydrated hydronium ion, as shown in Figure 1.4.

Figure 1.4 Hydronium ion in solution, surrounded by three hydrogen-bonded water molecules.

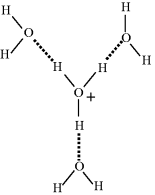
Table 1.7 gives the electrical mobility values for various ions in water, from which we learn that the apparent rate of migration of the H₃O⁺ ion in an electrical field is significantly greater than that exhibited by Na⁺ and K⁺ ions. We have discussed how the electrostatic binding energy of the proton is so large that it has no independent existence in condensed phases such as water. In water it is generally considered to be present as hydronium, H₃O⁺, which gives it an equivalent size between that of the hydrated sodium and potassium ion. The electrical mobility μ of an ion is defined as μ = v/E, where v is the terminal speed acquired under the influence of an electric field E. To a good approximation we can assume that the terminal speed is reached when the accelerating force (F_a = qE) is balanced by the Stokes viscous drag force. This viscous force is directly proportional to the size of the ion, and so the electrical mobility of a proton should be of the same magnitude as the Na⁺ and K⁺ ions.

Table 1.7 The electrical mobility of some ions at 25 °C in dilute aqueous solution [8].

How do we account for the anomalously high proton mobility? The accepted viewpoint is that a transport process, known as the Grotthuss mechanism, is responsible. This mechanism is named after Theodor Grotthuss [9], who suggested that electrical conduction through water resulted from the oxygen atoms simultaneously receiving and passing along a single hydrogen atom. An interesting aspect of this is that at the time of his proposal a water molecule was considered to be OH instead of H₂O, and that an understanding of ions in solution (let alone hydrogen bonds) was at a very primitive level. Nevertheless, his description that throughout the conduction process ‘only the water molecules located at the tip of the conducting wires will be decomposed, whereas all those located at intermediate positions will exchange their composing principles reciprocally and alternatively, without changing their nature’ proved to be remarkably insightful. The modern version of the Grotthuss mechanism is depicted in the sequence of events below. The first step involves the injection and binding of a proton into a hydrogen-bond network:

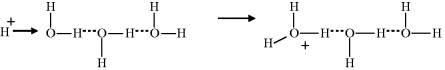
Subsequent steps involve the localised rearrangement of protons and hydrogen bonds, followed by the release of a proton from the hydrogen-bond network:

The final step is the reorientation of the water molecules to re-establish the hydrogen-bonded water structure that existed before the injection of a proton.

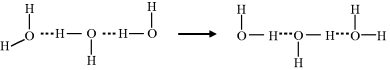
A partial analogy for the Grotthuss mechanism is the operation of a bucket brigade, where the buckets move but the people do not. Proton conduction does not involve the diffusion of either the hydronium ions or the protons themselves! A better analogy is electronic conduction along a copper wire. As an electron is injected into the end of a wire at a cathode, another electron is simultaneously ejected from the other end into the anode. This mode of proton transport is of relevance to bioenergetic processes that involve proton diffusion in protein complexes and the pumping of protons across cell membranes, and is the subject of ongoing research [10].

1.4 Acids, Bases and pH

According to the classical BrØnsted-Lowry definition of acid and base, H₃O⁺ is acidic (it can donate a H⁺ ion) and OH⁻ is basic or alkaline (it can accept a H⁺ ion). This definition is named after J.N. BrØnsted and T.M. Lowry (Danish and English physical chemists, respectively) who in 1923 independently formulated the protonic definition of acids and bases. Thus, any substance that can form a H⁺ ion is termed an acid, and any substance that combines with, and thus decreases the concentration of, H⁺ ions is termed a base. An acid-base reaction always involves such a so-called conjugate acid-base pair – the proton donor and the proton acceptor (H₃O⁺ and OH⁻, respectively, for the case of water). Water is said to be amphoteric because it acts either as acid or base. Examples of some acids and bases are given in Table 1.8.

Table 1.8 Acids and Bases.

The dissociation of water into acid and base is an equilibrium process that follows the Law of Mass Action, which states that the rate of a chemical reaction is proportional to the active masses of the reacting substances. For example, the equilibrium constant for the dissociation of water is given by:

(1.4) equation

where the brackets denote concentrations in moles per litre. To derive the final right-hand expression of this equation, we have divided the numerator and denominator by [H₂O]. The concentration of water remains virtually unaltered by its partial dissociation, since (at 25 °C) a litre of pure water contains only 1.0 × 10⁻⁷ M of H⁺ and an equal number of OH⁻ ions, whereas the concentration of water in a litre (1000 gm) of pure water is 1000 gm/L divided by the gram molecular weight (18 gm/mol) – namely 55.5 M. Thus, the concentration of water is virtually a constant and it makes no real sense to include it in equation (1.4) as if it were a variable. Equation (1.4) can thus be simplified to:

(1.5) equation

The constant K_eq can be combined with the concentration of water (55.5 M) to give a constant K_w termed the ion product of water. From Equation (1.5) at 25 °C, this is given by:

If [H⁺] for some reason increases, as when an acid substance is dissolved in water, [OH⁻] will decrease so as to keep the product [H⁺] [OH⁻] = 10⁻¹⁴.

This reaction is the basis for the pH scale, measured as a concentration of H⁺ (actually H₃O⁺). As shown in the Table 1.9 the pH scale is logarithmic, and typically covers the [H⁺] range from 1 M to 10⁻¹⁴ M. The term pH can be thought of as a shorthand term for the negative log of hydrogen ion concentration. It is defined as:

(1.7) equation

Table 1.9 The pH Scale.

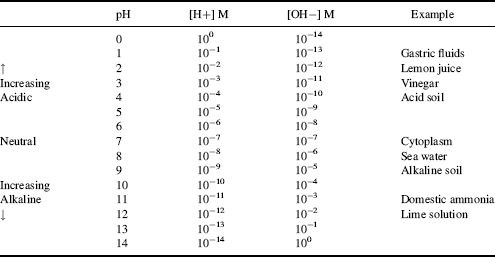
Thus, a 10⁻³ M solution of a strong acid, such as HCl, which dissociates completely in water, has a pH of 3.0, and so on for other concentrations. A solution in which [H⁺] = [OH⁻] = 10⁻⁷ M has a pH of 7.0, and is said to be neutral – that is, neither acidic nor basic.

1.4.1 The Biological Importance of pH

The hydrogen ion and hydroxyl ion concentrations are important in biological systems because protons are free to move from the H₃O⁺ to associate with and thereby neutralise negatively charged groups. Hydroxyl, OH⁻, ions are also available to neutralise positively charged groups. This ability to neutralise is especially important in proteins, which as discussed in the next chapter contain both carboxyl (ߝCOOH) and amino (ߝNH₂) side groups. The acidic carboxyl group can dissociate to give an ionised ߝCOO⁻ and H⁺, whereas the basic amino groups can accept a proton to give NH₃⁺. If the acidity of a protein solution is increased (i.e. pH lowered) there will be a relatively large number of H⁺ in the solution, so that the probability of a proton neutralising a carboxyl group (ߝCOO⁻ + H⁺ → ߝCOOH) will be greater than the probability of a hydroxyl ion removing the extra proton from an ionised amino group. Raising the pH of the solution (making it basic) will have the opposite effect. At a certain pH of the solution (the isoelectric point), depending on the relative number of carboxyl and amino side-groups, the net charge of a protein molecule will be zero. The electrical properties of proteins (e.g. electrophoretic mobility and electrostatic interactions) are thus determined by the pH of their environment. This is especially evident in the altered properties of an enzyme, because the binding of a substrate molecule to the active site of an enzyme generally involves electrostatic interactions. For example, the pH of the interior (i.e. the cytoplasm) of cells is normally ~7.2. Animal cells contain organelles, such as lysosomes, inside which the pH can be as low as 5. This pH value has been tuned to maximise the functioning of specialised enzymes that degrade proteins, nucleic acids and lipids.

1.4.2 The Henderson-Hasselbalch Equation

The generalised expression for the dissociation of an acid into a proton H⁺ and its anion A⁻ is given by:

(1.8) 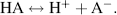equation

Some acids such as HCl dissociate completely and the reaction given above goes to completion:

(1.9) 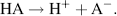equation

Other acids such as acetic acid dissociate only partially. In such cases an acid dissociation equilibrium is established with a significant amount of undissociated acid [AH] being present. The acid dissociation constant K_a is derived from the Law of Mass Action:

(1.10) 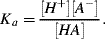equation

Taking the log of both sides of this equation, we obtain:

Substituting pH for −log [H⁺] and pK_a for −log K_a we obtain:

(1.11) equation

This is the Henderson-Hasselbalch equation, which permits the calculation of the degree of dissociation of an acid, given the pH of the solution and the pK_a of the acid. Exercises in the use of this equation are given in the problems section at the end of this chapter. Acids, such as hydrochloric, nitric and sulphuric, which ionise completely when added to water are classified as strong acids. The pH of their aqueous solutions is determined simply from their concentration in water using the relationship pH = −log[acid] as given by Equation (1.7). Likewise, the pH of a strong base is given by pH = 14 + log[base]. Acids that do not ionise completely are classified as weak acids, and as a rough guide have pK_a values greater than around 1.0. It is possible to have a concentrated solution of a weak acid, or a dilute solution of a strong acid. Most acids formed of organic molecules are weak acids. A good example is ethanoic acid, commonly known as acetic acid, having a pK_a value of 4.76 and which reacts with water to produce ethanoate and hydronium ions:

However, the back reaction is more dominant than the forward one – the ions react to reform the acetic acid and water. Only a small fraction of the acetic acid molecules are converted into ions, and the rest remain undissociated. Just because an acid may be classified as a weak one, this does not imply that it is relatively safer to handle. For example, hydrofluoric acid with a pK_a value of 3.15 is a weak acid that ionises in water according to the standard manner:

However, hydrofluoric acid is extremely toxic. It readily penetrates through the skin and then reacts with calcium and magnesium ions in the blood and tissues, resulting in a serious imbalance of these important physiological ions that can lead to damage, sometimes fatal, to nerves and the heart. Furthermore, when hydrofluoric acid approaches a concentration of 100% its acidity dramatically increases as a result of the following reaction:

From Table 1.4 we see that fluorine has a large (the largest) electronegativity value, which means that the toxic FHF⁻ anion is stabilised by a very strong HߝF hydrogen bond. Bioelectronics engineers are quite likely to come across hydrofluoric acid during the microfabrication of sensors and lab-on-chip devices, because it is used to dissolve the oxide on silicon wafers, and to etch channels in glass substrates, for example. So be warned!

The form of Equation (1.11) can be represented as a titration curve, to show the fraction of undissociated acid as a function of pH. Examples for acetic acid and lactic acid are shown in Figure 1.5.

Figure 1.5 Titration curves for acetic acid (pK_a = 4.76) and lactic acid (pK_a = 3.86).

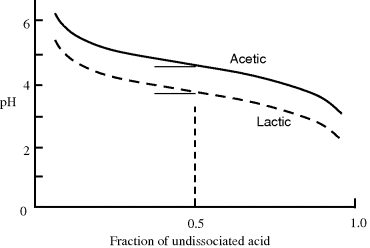
The pK_a of any acid is equal to the pH at which half of the acid molecules are dissociated and half are not. This can be verified by noting that for pH = pK_a, then from Equation (1.11) we have log([A⁻]/[HA] = 0, corresponding to [A⁻] = [HA]. At one pH unit below its pK_a value, 91% of an acid's molecules will not be dissociated and will be present as [HA]. At one pH unit above its pK_a, 91% of an acid will be in the [A⁻] form.

Some acids have more than one chemical group that can act as a proton donor. An example of a biologically important acid is phosphoric acid:

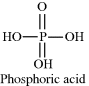
The three OH groups in the phosphoric acid molecule do not dissociate simultaneously to act as proton donors, but do so with discrete pK_a constants according to the following three reactions taken in order:

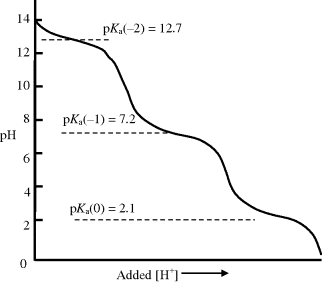
The variation of the pH of an aqueous solution of phosphoric acid (H₃PO₄) at 298 K, as a function of an added acid, is shown in Figure 1.6. The effect of the separate dissociations of its three hydrogen atoms can clearly be seen in this titration curve. On adding another acid to the phosphoric acid solution, the pH of the solution decreases. At a pK_a value, however, the increase of pH is less than if the phosphoric acid had been absent, because protons released into the solution by the additional acid are taken up by the ionised (A⁻) form of the phosphoric acid. Likewise, if we have an acid of pH value near to its pK_a value and add to it an alkali (base) such as sodium hydroxide (NaOH), the pH will increase but at a slower rate than if the phosphoric acid was absent. Hydroxyl ions generated by the added base are neutralised by protons released by the phosphoric acid. This property of an acid or base is known as buffering, and as shown in Figures 1.5 and 1.6, the ability to act in this way decreases rapidly for pH values one unit above or below the pK_a.

Figure 1.6 The titration curve for phosphoric acid (H₃PO₄) at 298 K, as a function of an added acid. As discussed in the text, the greatest buffering capacity of a conjugate acid-base system is obtained when pH = pK.

Phosphate forms part of the structure of DNA and RNA, and is linked to two carbon atoms of adjacent ribose sugars. The OH group can dissociate to give a free proton – hence the reason why DNA and RNA molecules are classified as acids. The dissociation process is depicted below:

The pK_a for the dissociation of the OH proton in DNA and RNA is ~3.0, and so at physiological pH (~7.2) each phosphate residue in DNA or RNA is negatively charged.

1.4.3 Buffers

Because of the effect of pH on the ionisation of basic and acidic groups in proteins and other biological molecules, the pH of intra- and extracellular fluids must be held within the narrow limits in which the enzyme systems have evolved. Deviations of one pH unit or more generally disrupt the orderly functioning of a living system. This sensitivity to the acidity of the aqueous intracellular milieu exists in part because reaction rates of different enzyme systems become mismatched and uncoordinated. For example, the pH of human blood is maintained at pH 7.4 by means of natural pH buffers. As discussed above, a buffered system is one that undergoes little change in pH over a certain pH range upon addition of relatively large amounts of an acid or a base.

A buffer must contain an acid [HA] to neutralise added bases, and a base [A⁻] to neutralise added acids. The greatest buffering capacity of such a conjugate acid-base pair occurs when the acid [HA] and base [A⁻] concentrations are both large and equal. Referring to the Henderson-Hasselbalch equation (1.11) we see that this situation exists when the pH is equal to the pK_a of the acid component of the buffering system (since log 1 = 0). This is demonstrated in Figures 1.3 and 1.4 for that portion of a titration curve along which there is relatively little change in pH on addition of hydroxide.

The most effective buffer systems are combinations of weak acids and their salts. The former dissociate only slightly, thus ensuring a large reservoir of HA, whereas the latter dissociate completely, providing a large reservoir of A⁻. Added H⁺ therefore combines with A⁻ to form HA, and added OH⁻ combines with H⁺ to form HOH. As H⁺ is thereby removed, it is replaced by dissociation of HA. The most important inorganic buffer systems in the body fluids are the bicarbonates and phosphates. Amino acids, peptides and proteins, because of their weak-acid side groups, form an important class of organic buffers within and outside biological cells. An acid-base indicator is often added to the medium used to culture cells in the laboratory. These indicators are often large soluble organic molecules whose colour in its acid form (when combined with a hydrogen) differs from that when it is in its anionic, conjugate base, form. The indicator molecule is chosen to have a pK_a value close to the pH (e.g. pH 7.4) at which the medium is to be maintained.

A list of common buffering systems and their corresponding useful buffering pH ranges are given in Table 1.10.

Table 1.10 Some common buffering systems and their useful buffering pH ranges.

Buffering system	Useful buffering range
Hydrochloric acid and potassium chloride	pH 1.0 – pH 2.2
Hydrochloric acid and glycine	pH 2.2 – pH 3.6
Citric acid and sodium citrate	pH 3.0 – pH 6.2
Acetic acid and sodium acetate	pH 3.7 – pH 5.6
Sodium hydroxide and potassium dihydrogen phosphate	pH 5.8 – pH 8.0
Sodium tetraborate and hydrochloric acid	pH 8.1 – pH 9.2
Sodium hydroxide and glycine	pH 8.6 – pH 10.6
Sodium hydroxide and sodium bicarbonate	pH 9.6 – pH 11.0
Sodium hydroxide and sodium hydrogen phosphate	pH11.0 – pH 11.9
Sodium hydroxide and potassium chloride	pH 12.0 – pH 13.0

Phosphate buffers are also commonly used, and these are prepared by adding set amounts of 0.1 M disodium hydrogen phosphate to either defined amounts of 0.1 M hydrochloric acid to obtain buffers covering the range pH 7 to pH 9, or to defined amounts of sodium hydroxide to cover the range pH 10 to pH 11.

1.5 Summary of Key Concepts

Biological systems are able to perform chemical transformations that produce fluxes of matter and energy to maintain a highly organised molecular system that is far from being in thermodynamic equilibrium with its environment. Because biological systems function at constant temperature, they cannot utilise the flow of heat as a source of energy to achieve this state. Instead, they utilise the potential energy stored in chemical covalent bonds. The energy of most value to biological systems is the change in Gibbs free-energy ΔG of a chemical reaction. Biological systems utilise the free-energy released from the chemical bonds of molecules such as adenosine triphosphate (ATP) or glucose, and couple these reactions with those that synthesise proteins and other required substances, and to reactions that perform work such as muscle contraction or the pumping of ions against their chemical gradients across membranes.

Covalent chemical bonds are formed when electronic orbitals are shared between two atoms. The extent to which electronic charge is shared between the bonded atoms depends on their relative values of electronegativity. In polar bonds more electronic charge is located near the more electronegative atom which assumes a small negative charge, and the atom of lower electronegativity takes on an equal but slightly positive charge. Water molecules are formed of two polar OߝH bonds, and this leads to mutual attractions of its molecules through a network of hydrogen bonds. Without these hydrogen bonds water would not exist as a liquid on earth, but as a gas. The polar form of a water molecule, and the hydrogen-bonded network, lend to liquid water a large value of relative permittivity (dielectric constant). This gives liquid water excellent properties as a solvent for ionic salts (weakening ionic bonds to the point where the ionic crystal lattice dissociates into free ions) and the ability to dissolve nonionic substances that possess polar chemical bonds (e.g. sugars and alcohol molecules) by forming hydrogen bonds with them. Organic molecules that are nonpolar and nonionic are not soluble in water.

A water molecule can dissociate by breaking one of its HߝO bonds into a positively charged hydrogen ion (proton) and a negatively charged hydroxyl ion. Although hydrogen ions rapidly combine with water molecules to form hydronium ions (H₃O⁺), it is useful to consider them in their nascent form and to refer to the concentration [H⁺] of hydrogen ions in a solution – expressed as the pH of the solution (pH = −log[H⁺]). In pure water at 298 K, [H⁺] = 10⁻⁷ M, to give a pH value of 7.0. The pH of a biological fluid, such as the cytoplasm inside a cell or fluid within intracellular organelles, is an important parameter controlling the biochemical reactions that maintain the viability of a living system. Biological systems employ different types of organic and inorganic molecules as pH buffers to maintain biological fluids at their optimal pH.

Certain combinations of atoms, such as the hydroxyl (ߝOH), carboxyl (ߝCOOH), carbonyl (ߝC=O), and amino (ߝNH₂) groups, are common components of biologically important molecules. Each one of these groups has distinct chemical properties associated with their tendency to gain or lose protons. An appreciation of this greatly simplifies an understanding of many aspects of the chemistry of living systems.

Problems

1.1. What is meant by equilibrium in a chemical reaction?

1.2. Explain how you would prepare the following aqueous solutions:

a. 100 mL of 0.1 M NaCl

b. 10 mL of 50 mM KCl

c. 100 mL of 1 M MgCl₂ (from a bottle of the anhydrous salt)

d. 100 mL of 1 M MgCl₂ (from a bottle of the hydrate MgCl₂(H₂O)₃).

e. 2 μM KCl solution.

1.3. What are the properties of water that make it a good solvent for ions and molecules in a cell?

1.4. Describe the formation of hydrogen bonds in water. If water did not contain hydrogen bonds would it exist as a solid, liquid or gas at room temperature?

1.5. Hydrochloric acid is an example of a strong acid, and sodium hydroxide is classed as a strong base. They can be assumed to fully dissociate (ionise) when dissolved in water. On this basis, calculate the pH of the following solutions:

a. 1 M HCl

b. 1 μM HCl

c. 10 mM NaOH.

1.6. A 1 M solution of acetic acid (pK_a = 4.75) has a pH of 2.4. What percentage of the acetic acid molecules is dissociated? Is acetic acid a strong or weak acid? (Domestic vinegar comprises ~1 M acetic acid.)

1.7. Lactic acid (C₃H₆O₃) in solution can lose a proton from its acidic group to produce the lactate ion CH₃CH(OH)COO⁻. Calculate the pK_a of lactic acid, given that when the concentration of lactic acid is 0.01 M and the concentration of lactate is 0.087 M, the pH is 4.8.

1.8. Using the Henderson-Hasselbalch equation, and by defining a base concentration factor α as

show that the greatest buffering capacity of a conjugate acid-base pair occurs for [A⁻] = [HA]. (Hint: Find the value for α where d(pH)/dα has its lowest value.)

References

1. Lewis, G.N. (1916) The atom and the molecule. Journal of the American Chemical Society, 38, 762–785.

2. Pauling, L. (1960) Chapter 2, in The Nature of the Chemical Bond, 3rd edn, Cornell University Press.

3. Lennard-Jones, J.E. (1931) Cohesion. Proceedings of the Physical Society, 43, 461–482.

4. Pauling, L. (1932) The nature of the chemical bond, IV: the energy of single bonds and the relative electronegativity of atoms. Journal of the American Chemical Society, 54, 3570–3582.

5. Bondi, A. (1964) Van der Waals volumes and radii. Journal of Physical Chemistry, 68, 441–451.

6. Housecroft, C.E. and Constable, E.C. (2010) Chapter 4, in Chemistry, 4th edn, Prentice Hall.

7. Schrödinger, E. (1944) What is Life? Cambridge University Press.

8. Atkins, P.W. and De Paula, J. (2002) Chapter 27, in Physical Chemistry, 7th edn, W.H. Freeman.

9. de Grotthuss, C.J.T. (1806) Mémoire sur la décomposition de l'eau et des corps qu'elle tient en dissolution à l'aide de l'électricité galvanique. Annales de Chimie (Paris), 58, 54–74. An English translation, by Régis Pomès, of this paper is published in: Biochimica et Biophysica Acta 1757: 871–875, 2006.

10. Wraight, C.A. (2006) Chance and design: Proton transfer in water, channels and bioenergetic proteins. Biochimica et Biophysica Acta, 1757, 886–912.