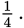
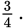 Again, if this is a whole number, take the mean of this position and the next. If
it is a decimal, round up to the next whole number, and take that as the quartile
position.
Again, if this is a whole number, take the mean of this position and the next. If
it is a decimal, round up to the next whole number, and take that as the quartile
position.
After Chapter 12.3, you will be able to:
Distributions can be characterized not only by their “center” points, but also by the spread of their data. This information can be described in a number of ways. Range is an absolute measure of the spread of a data set, while interquartile range and standard deviation provide more information about the distance that data falls from one of our measures of central tendency. We can use these quantities to determine if a data point is truly an outlier in our data set.
The range of a data set is the difference between its largest and smallest values:
Range does not consider the number of items of the data set, nor does it consider the placement of any measures of central tendency. Range is therefore heavily affected by the presence of data outliers. In cases where it is not possible to calculate the standard deviation for a normal distribution because the entire data set is not provided, it is possible to approximate the standard deviation as one-fourth of the range.
Interquartile range is related to the median, first, and third quartiles. Quartiles, including the median (Q2), divide data (when placed in ascending order) into groups that comprise one-fourth of the entire set. There is some debate over the most appropriate way to calculate quartiles; for the purposes of the MCAT, we will use the most common (and simplest) method:
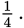
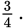 Again, if this is a whole number, take the mean of this position and the next. If
it is a decimal, round up to the next whole number, and take that as the quartile
position.
Again, if this is a whole number, take the mean of this position and the next. If
it is a decimal, round up to the next whole number, and take that as the quartile
position.
The interquartile range is then calculated by subtracting the value of the first quartile from the value of the third quartile:
The interquartile range can be used to determine outliers. Any value that falls more than 1.5 interquartile ranges below the first quartile or above the third quartile is considered an outlier.
One definition of an outlier is any value lower than 1.5 × IQR below Q1 or any value higher than 1.5 × IQR above Q3.
Standard deviation is the most informative measure of distribution, but it is also the most mathematically laborious. It is calculated relative to the mean of the data. Standard deviation is calculated by taking the difference between each data point and the mean, squaring this value, dividing the sum of all of these squared values by the number of points in the data set minus one, and then taking the square root of the result. Expressed mathematically
where σ is the standard deviation, xi to xn are the values of all of the data points in the set,
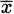 is the mean, and n is the number of data points in the set. The use of n − 1 instead of n is mathematically—but not practically—important and the reason for doing so is beyond
the scope of the MCAT.
is the mean, and n is the number of data points in the set. The use of n − 1 instead of n is mathematically—but not practically—important and the reason for doing so is beyond
the scope of the MCAT.
The standard deviation can also be used to determine whether a data point is an outlier. If the data point falls more than three standard deviations from the mean, it is considered an outlier. The standard deviation relates to the normal distribution as well. On a normal distribution, approximately 68% of data points fall within one standard deviation of the mean, 95% fall within two standard deviations, and 99% fall within three standard deviations, as shown in Figure 12.1 earlier. Integration or specialized software can be used to determine percentages falling within other intervals.
Another definition of outlier is any value that lies more than three standard deviations from the mean.
While we have already discussed methods for determining if a data point is an outlier, it is useful to know how to approach data with outliers. Outliers typically result from one of three causes:
When an outlier is found, it should trigger an investigation to determine which of these three causes applies. If there is a measurement error, the data point should be excluded from analysis. However, the other two situations are less clear.
The existence of outliers is key for determining whether or not the mean is an appropriate measure of central tendency. It may also indicate a measurement error on the part of the investigators.
If an outlier is the result of a true measurement, but is not representative of the population, it may be weighted to reflect its rarity, included normally, or excluded from the analysis depending on the purpose of the study and preselected protocols. The decision should be made before a study begins—not once an outlier has been found. When outliers are an indication that a data set may not approximate the normal distribution, repeated samples or larger samples will generally demonstrate if this is true.