1.11 Moto circolare

Figura 1.21

Si chiama moto circolare un moto piano la cui traiettoria è rappresentata da una circonferenza. Considerando che la velocità varia continuamente in direzione l’accelerazione centripeta è sempre diversa da zero (e quindi agisce una forza, detta centripeta, diretta verso il centro della circonferenza). Nel moto circolare uniforme la velocità è costante in modulo e l’accelerazione tangente è nulla per cui a = a_N ; se invece il modulo della velocità cambia nel tempo il moto circolare non è uniforme e a_T è diversa da zero; in questo caso la direzione dell’accelerazione non passa per il centro della circonferenza (oltre alla forza centripeta agisce anche una forza tangenziale).

Il moto circolare può essere descritto facendo riferimento allo spazio percorso sulla circonferenza s(t) oppure utilizzando l’angolo θ(t) sotteso dall’arco s(t), con θ(t) = s(t) /R.

L’assumere come variabile l’angolo θ(t) significa in sostanza porsi in un sistema di coordinate polari di centro in O in cui il moto avviene con r(t) = R = costante e θ(t) variabile. Anche la rappresentazione in coordinate cartesiane è legata come sappiamo a θ(t) : x(t) = R cos θ(t), y(t) = R sen θ(t).

Siamo naturalmente interessati alle variazioni dell’angolo nel tempo e pertanto definiamo la velocità angolare come la derivata dell’angolo rispetto al tempo:

Velocità angolare

Risulta che la velocità angolare è proporzionale alla velocità con cui è descritta la circonferenza; se v è variabile lo è anche ω.

Ricollegandoci a (1.19), nel moto circolare la velocità radiale è identicamente nulla perché il raggio vettore è costante in modulo e la velocità trasversa coincide con la velocità: da $v_{\theta }=r\frac{d\theta }{dt}$ ritroviamo v = Rω (tutto ciò è vero se l’origine coincide col centro della circonferenza).

Il moto circolare più semplice è quello uniforme: v e ω sono costanti e le leggi orarie, con riferimento alle due variabili utilizzate, si scrivono

Ripetiamo che il termine uniforme significa esclusivamente costanza del modulo della velocità; il moto circolare uniforme è un moto accelerato con accelerazione costante, ortogonale alla traiettoria,

Si tratta inoltre di un moto periodico con periodo $T=\frac{2\pi R}{v}=\frac{2\pi }{\omega }$ , corrispondente al tempo necessario per compiere un giro completo. I moti proiettati sugli assi cartesiani sono

cioè due moti armonici di eguale ampiezza e fase iniziale, sfasati tra loro di π/2, e con periodo coincidente con quello del moto circolare uniforme. Numericamente la velocità angolare è eguale alla pulsazione, anche se il significato fisico delle due grandezze è diverso.

Nel caso del moto circolare non uniforme oltre all’accelerazione centripeta, che è variabile perché la velocità varia anche in modulo, dobbiamo considerare anche l’accelerazione tangenziale a_T = dv/dt. Siccome è variabile anche ω definiamo l’accelerazione angolare

Accelerazione angolare

Se è nota la legge oraria angolare θ(t) con le due derivazioni successive (1.25) e (1.27) determiniamo le variazioni dell’angolo e della velocità angolare. Viceversa, nota la funzione α(t), possiamo integrare ottenendo:

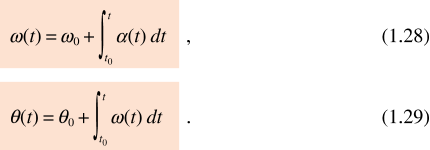
Qualora in un particolare problema sia nota la funzione α(θ), invece di α(t), possiamo calcolare l’incremento della velocità angolare in corrispondenza all’incremento angolare θ – θ₀ . Infatti

Si noti ancora una volta come siano importanti, quando si integra, le condizioni iniziali, cioè i valori di ω e θ nell’istante iniziale o di ω nella posizione iniziale.

Un caso particolare di moto circolare non uniforme è costituito dal moto circolare uniformemente accelerato in cui α = costante ovvero a_T = costante. Da (1.28) e (1.29) abbiamo, posto t₀ = 0,

L’accelerazione centripeta vale a_N = ω ² R = (ω₀ + α t)² R.

Si sarà certamente notata la completa analogia matematica tra la trattazione del moto rettilineo e quella del moto circolare fatta tramite θ(t): il significato fisico e la geometria sono diversi, ma le equazioni a cui si arriva hanno la stessa struttura. Ciò deriva dal fatto che con la scelta della descrizione angolare abbiamo ridotto un problema bidimensionale a un problema unidimensionale. Mentre però nel moto rettilineo la descrizione unidimensionale è ovviamente completa, nel moto circolare con ω(t) e α(t) descriviamo solo l’evoluzione temporale del moto, che è legato esclusivamente al modulo della velocità, e non rendiamo conto delle variazioni di direzione che portano all’accelerazione centripeta. E infatti 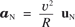è stata calcolata con un ragionamento giustamente bidimensionale nel paragrafo 1.9.

Ad ogni modo, la comodità dell’uso di θ(t) è innegabile, perché si risolvono i problemi di moto circolare con formule analoghe a quelle del moto rettilineo; basta poi ricordare che istante per istante ad a_Τ = α R u_Τ bisogna sommare vettorialmente a_N = ω ² R u_N per avere il corretto valore dell’accelerazione (e quindi il corretto legame con le forze agenti).

Esempio 1.9

Descrivere il moto circolare in cui α = – kω, con k costante positiva.

Soluzione

È un moto circolare vario, con equazione differenziale

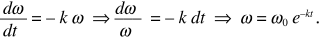
Il moto è smorzato esponenzialmente (vedi paragrafo 1.7). Da (1.30) si ricava inoltre ω(θ) = ω₀ – kθ e si calcola l’angolo di arresto θ = ω₀ /k.

Visualizza soluzione

Esempio 1.10

Descrivere il moto circolare in cui α = – k²θ.

Soluzione

È ancora un moto vario, che obbedisce all’equazione $\frac{d^2\theta }{d{t}^2}+k^2\theta =0$ la soluzione è θ = θ₀ sen (kt + Φ). Il punto descrive un arco di circonferenza di ampiezza angolare 2θ₀ con moto armonico semplice. La velocità angolare di questo moto è $\omega =\frac{d\theta }{dt}+k{\theta }_0\cos \left(kt+\varphi \right)$ , variabile nel tempo; la pulsazione è , costante.

Visualizza soluzione

Esempio 1.11

Un punto materiale si muove lungo una circonferenza di raggio R = 1.8 m con accelerazione angolare α₁ = 2.39 rad/s²; all’istante t = 0 θ = 0 e ω = 0. Dopo aver percorso mezzo giro il moto del punto diventa uniformemente decelerato ed esso si ferma dopo aver percorso un altro mezzo giro. Calcolare l’accelerazione angolare α₂ durante il secondo mezzo giro e il tempo totale impiegato a percorrere il giro completo. Se nello stesso intervallo di tempo il moto fosse uniforme, quale sarebbe l’accelerazione centripeta del punto?

Soluzione

Alla fine del primo mezzo giro (θ = π), secondo (1.30) si ha

Nel secondo mezzo giro, da π a 2π, alla fine del quale il punto si ferma, analogamente si ha

e quindi α₂ = – α₁ = – 2.39 rad/s², com’era intuibile.
Il tempo impiegato a percorrere il primo mezzo giro si ricava da

Il tempo totale è 2 t₁ = 3.24 s.
Se il moto fosse uniforme sarebbe ω = π / t₁ = 1.94 rad/s, a_N = ω² R = 6.77 m/s².

Visualizza soluzione

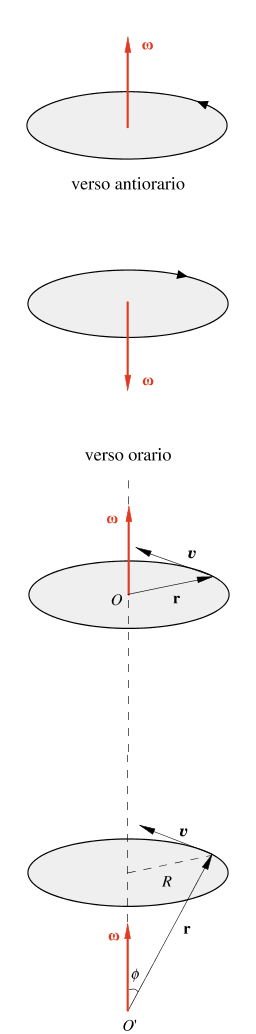
Figura 1.22

Notazione vettoriale

Ampliamo il concetto di velocità angolare del moto circolare mostrando come le si possono associare caratteristiche vettoriali. Si definisce velocità angolare il vettore ω che ha queste proprietà: il modulo è ω = dθ/dt, la direzione è perpendicolare al piano in cui giace la circonferenza e il verso è tale che dall’estremo del vettore ω il moto appaia antiorario (vedi figura 1.22). In base alla definizione risulta evidente che

Di norma ω si pensa applicata nel centro della circonferenza, nel qual caso r = R. La (1.31) resta però valida se ω è applicata in un qualsiasi altro punto dell’asse di rotazione (retta ortogonale al piano del moto e passante per il centro della circonferenza); infatti direzione e verso di v restano eguali e il modulo vale ancora v = ω r sen Φ = ω R.

Se diamo ω, individuiamo pertanto l’asse di rotazione e il piano del moto circolare, con quale verso è percorsa la circonferenza e come varia l’angolo nel tempo. Da ω, per derivazione rispetto al tempo, si ottiene il vettore accelerazione angolare α che risulta parallelo a ω, dato che questa ha direzione costante, e ha verso determinato dalla variazione del modulo di ω e modulo α = dω/dt.

Tramite α e ω si può esprimere l’accelerazione del moto circolare:

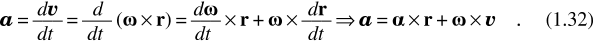
Il primo termine α × r è l’accelerazione tangenziale α_Τ (modulo αR), il secondo ω × v è l’accelerazione centripeta α_N (modulo ω ² R).

Nel moto circolare uniforme w è un vettore costante anche in modulo, α è nulla e α = α_N = ω × v.

Osservando la figura 1.22 notiamo una proprietà importante: il vettore r applicato in O' ha modulo costante e descrive un moto rotatorio attorno all’asse di rotazione, ovvero alla direzione di ω, formando un angolo Φ costante con l’asse stesso; la sua derivata dr/dt si può scrivere ω × r. Anche il vettore v, che nel moto circolare uniforme ha modulo costante, descrive una rotazione attorno ad ω, con cui forma l’angolo Φ = π / 2, e la sua derivata dv/dt si può scrivere ω × v. A questo tipo di moto, rotazione di un asse rispetto ad un altro asse fisso, con cui forma un angolo costante e ha un punto in comune, si dà il nome di moto di precessione.

La proprietà importante è la seguente: dato un vettore di modulo costante A, che descrive un moto di precessione con velocità angolare ω, la sua derivata temporale può sempre essere scritta

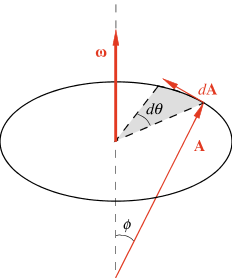
Figura 1.23

Vediamo che $\frac{d\text{A}}{dt}$ risulta ortogonale ad A come deve essere per un vettore di dt modulo costante (vedi appendice C); inoltre, per quanto riguarda direzione e verso, la (1.33) si verifica subito guardando la figura 1.23; in modulo, dA = A senΦ dθ e dA/dt = A senΦ dθ/dt = ω A senΦ = | ω × A |.

Abbiamo considerato finora solo un moto circolare che si svolge sempre nello stesso piano; più in generale può avvenire che per un tempo dt la rotazione avvenga rispetto ad un certo asse e in un istante successivo rispetto ad un altro asse, cioè che ω sia funzione del tempo anche in direzione; pure in tal caso (1.33) resta valida.

Unità di misura

velocità angolare      rad/s = rad s^–1      accelerazione angolare      rad/s² = rad s^–2