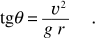
2.12 Forze centripete

Supponiamo che la risultante R delle forze agenti su un punto materiale presenti una componente F_N ortogonale alla traiettoria, che risulta pertanto curvilinea (si riveda la parte finale del paragrafo 2.6). F_N determina l’accelerazione centripeta secondo la relazione F_N = m a_N = m v²/r essendo r il raggio di curvatura della traiettoria.

In generale R ha anche una componente tangente alla traiettoria, F_T , responsabile della variazione del modulo della velocità. Se F_T = 0 il moto lungo la traiettoria è uniforme e l’unica accelerazione è a_N .

Forze centripete sono generalmente prodotte da rotaie, pneumatici, fili che collegano il corpo ad un punto fisso ovvero vincoli che consentono di incurvare la traiettoria oppure da azioni a distanza come quelle gravitazionali.

Figura 2.24

Esempio 2.14Curve sopraelevate

Si vuole determinare quale condizione deve essere soddisfatta affinché un punto materiale, lanciato con velocità v orizzontale lungo una curva sopraelevata, come quelle presenti in un velodromo, percorra a velocità costante un arco di circonferenza, in un piano orizzontale, con centro in O. La situazione è mostrata in figura 2.25a; la traiettoria è indicata dalla linea punteggiata nella vista in pianta.

Soluzione

Per ottenere un moto circolare uniforme la risultante delle forze applicate R deve essere ortogonale alla traiettoria e diretta verso il centro. Le forze agenti sono il peso del punto materiale mg e la reazione vincolare della pista N, normale alla superficie se il vincolo è liscio come supponiamo; esse devono essere disposte come nella figura 2.25b. La componente orizzontale di N, N senθ , rivolta verso il centro della traiettoria circolare seguita dal punto fornisce la forza centripeta: N senθ = m v²/r; d’altra parte per la condizione di equilibrio nella direzione verticale N cosθ = mg. Ricavando N da questa e sostituendo nella prima si ottiene

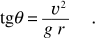
Per realizzare la condizione voluta devono soddisfare questa relazione la velocità con cui si affronta la curva, il raggio di curvatura e l’angolo di inclinazione della curva. Per esempio se θ = 30° e r = 30 m il punto resta a quota fissa percorrendo la curva con v ≅ 13 m/s = 46.8 Km/h. A velocità minori il punto scende verso il basso, a velocità maggiori sbanda verso l’alto.

La reazione N ha il valore mg/cosθ , maggiore del valore mg cosθ trovato nel piano inclinato. In effetti, oltre a dover reagire alla componente mg cosθ del peso, il suolo deve fornire la forza centripeta necessaria perché il moto sia circolare: la quantità di moto del punto cambia continuamente in direzione per effetto dell’interazione col suolo.

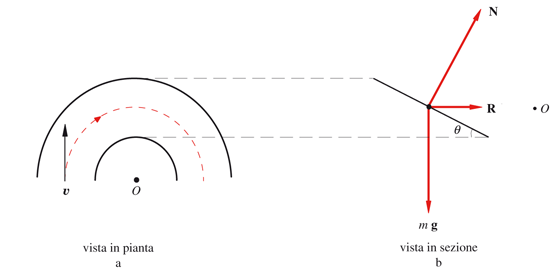
Figura 2.25

Visualizza Soluzione

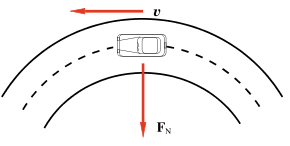
Figura 2.26 (Esempio 2.15)

Esempio 2.15Curva su strada piana

Vogliamo adesso studiare la velocità massima con cui un’auto può affrontare in una strada piana una curva di raggio r.

Soluzione

La forza centripeta necessaria è fornita dall’attrito tra pneumatici e terreno; poiché la traiettoria è un arco di circonferenza di raggio r non c’è spostamento lungo r e il coefficiente di attrito rilevante per il problema è quello statico. Pertanto il caso limite si ha per il valore massimo della forza di attrito, cioè per F_N = μ_s N = μ_s m g, e deve essere μ_s m g = m v²/r. La velocità massima con cui può essere affrontata la curva è

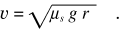
Con μ_s = 0.5 e r = 30 m si trova v = 12.1 m/s = 43.6 Km/h. Se invece la curva è su rotaia, la forza centripeta è fornita dal sistema che tiene fisse le rotaie al suolo.

Visualizza Soluzione

Figura 2.27 (Esempio 2.16)

Esempio 2.16Pendolo conico

Si abbia un punto materiale di massa m appeso in O (vedi fig. 2.27) tramite un filo inestensibile di massa trascurabile lungo L. Vogliamo determinare le condizioni per cui P descriva un moto circolare uniforme.

Soluzione

Sul punto P agiscono la forza peso m g e la forza T, dovuta al filo e diretta come questo (trascuriamo ogni attrito). Come nel primo esempio

da cui si ricava tgθ = v²/g r. Ponendo r = L senθ e v = ωr si ha

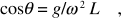
relazione che deve sussistere tra velocità angolare, lunghezza del filo e angolo rispetto alla verticale dello stesso affinché il punto P descriva un moto circolare uniforme. Al crescere di ω cresce il valore di θ; in ogni caso deve sussistere la condizione ω² ≥ g / L. Il valore della forza dovuta al filo, detta tensione del filo, è

Visualizza Soluzione

Una caratteristica comune agli esempi trattati è l’indipendenza dalla massa del punto delle varie condizioni trovate, come $tg\theta =v^2/gr,v=\sqrt{{\mu }_{s}gr},\cos \theta =g/{\omega }^{2}L.$ Questo perché in tutti gli esempi è presente soltanto la forza peso, che è proporzionale alla massa, e le reazioni vincolari, determinate dall’azione del peso e quindi anch’esse proporzionali alla massa del punto; eguagliando la risultante di tutte le forze a mα la massa viene semplificata e quindi il risultato cinematico è indipendente dalla massa (mentre, come detto, non lo sono le forze).

Equilibrio dinamico

Dopo questi esempi possiamo anche chiarire cosa intendiamo per equilibrio dinamico; a differenza dell’equilibrio statico descritto nel paragrafo 2.4 (risultante delle forze applicate al punto eguale a zero, velocità nulla), ci riferiamo a quei particolari casi in cui in presenza di forze il moto avviene con velocità costante in modulo. Se si tratta di moto rettilineo ciò è possibile solo se la risultante delle forze è nulla e abbiamo visto appunto i casi di moto uniforme in presenza di forze di attrito radente o di attrito viscoso, che bilanciano l’effetto della forza peso (paragrafi 2.8, 2.9, 2.11). Se invece il moto è curvilineo basta che sia nulla F_T , come deve essere se vogliamo che la velocità sia costante in modulo, ovvero che la risultante delle forze agenti sia puramente centripeta. Qualora F_N sia anche costante in modulo il moto è circolare uniforme, come negli esempi appena considerati.