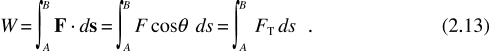
2.15 Lavoro. Potenza. Energia cinetica

Abbiamo visto come la legge di Newton (2.1) si esprime in termini integrali attraverso il teorema dell’impulso (2.3), rilevando che si arriva a determinare la variazione finita di quantità di moto solo se si può calcolare esplicitamente l’intetgrale . Affrontiamo adesso il problema dell’integrazione della legge di ∫ 0 Newton quando si considera la forza come funzione della posizione occupata dal punto, ampliando il ragionamento già fatto nel paragrafo 1.4 a proposito di a(x) e a(t) nel moto rettilineo.

Figura 2.40

Consideriamo un punto materiale che si muove lungo una generica traiettoria curvilinea e sia F la risultante delle forze agenti sul punto. Si definisce lavoro della forza F, compiuto durante lo spostamento del punto dalla posizione A alla posizione B, la quantità scalare

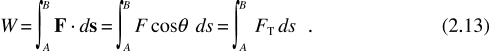
Il lavoro è l’integrale di linea della forza (appendice C), cioè è dato dalla somma di infiniti contributi infinitesimi dW = F · ds = F_T ds. Si osservi che in generale lungo la traiettoria sia F che θ sono variabili.

Si possono presentare tre casi. F forma con ds un angolo minore di π/2, per cui l’accelerazione tangente è concorde con la velocità e la fa aumentare: dW risulta positivo e viene chiamato lavoro motore. Oppure F forma con ds un angolo maggiore di π/2, il punto viene frenato e dW risulta negativo (lavoro resistente). Infine se F è ortogonale alla traiettoria, θ = π/2 e il lavoro è nullo: in questo caso F ha azione puramente centripeta e non fa variare il modulo della velocità. Lungo un arco finito di traiettoria può presentarsi sempre la stessa situazione, così che la velocità finale è maggiore di quella iniziale se θ < π/2, minore se θ > π/2 e eguale se θ= 0; oppure le varie situazioni possono alternarsi e il risultato dipende da quale situazione è predominante.

Quando F è effettivamente la somma di n forze F₁ , F₂ ,…, F_n , per ciascuna si può calcolare il corrispondente lavoro W_i e risulta W = Σ_i W_i :

Il lavoro è pari alla somma dei lavori delle singole forze agenti, ciascuno dei quali può essere positivo, negativo o nullo.

Secondo quanto detto sopra il lavoro totale può essere nullo in quanto somma di lavoro motore lungo un arco di traiettoria e di lavoro resistente lungo un successivo arco. Certamente però possiamo affermare che W = 0 quando non agisce nessuna forza oppure agiscono forze la cui risultante o è nulla o è sempre ortogonale alla traiettoria (condizioni di equilibrio dinamico, paragrafo 2.12). Un esempio di moto con risultante nulla delle forze è il moto rettilineo uniforme in presenza di attrito radente: occorre applicare una forza eguale e contraria alla forza di attrito e quindi fornire un lavoro motore eguale ed opposto al lavoro resistente dell’attrito. Invece un moto con risultante delle forze sempre ortogonale alla traiettoria è il moto curvilineo uniforme: se c’è attrito, oltre alla forza normale deve essere presente una forza tangente, che svolge un lavoro motore, per bilanciare l’effetto dell’attrito.

Potenza

La potenza corrisponde al lavoro per unità di tempo:

Potenza

Questa è la potenza istantanea, in generale variabile durante il moto, e caratterizza la rapidità di erogazione del lavoro.

La potenza media è il rapporto W/t, cioè il lavoro totale diviso per il tempo durante cui il lavoro è stato svolto. Tale grandezza risulta particolarmente importante per qualificare le prestazioni di un dispositivo o macchina che fornisce lavoro. A parità di lavoro totale svolto, ha maggiore potenza quella macchina che lo eroga in minore tempo.

Energia cinetica

Riprendiamo la relazione relativa al lavoro infinitesimo associato ad uno spostamento ds:

Abbiamo trovato così il legame esplicito tra il lavoro infinitesimo e la variazione infinitesima del modulo della velocità rendendo quantitativa la discussione fatta in precedenza. Per un percorso finito dalla posizione A a quella B abbiamo

Energia cinetica

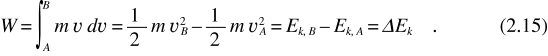
Il lavoro è eguale alla variazione della quantità ¹/₂ m v² che si chiama energia cinetica del punto materiale. Il simbolo ∆ indica valore finale meno valore iniziale. La (2.15), nota come teorema dell’energia cinetica, è stata ricavata utilizzando la legge di Newton e pertanto ha validità generale, qualunque sia la forza che agisce.

Se W > 0, l’energia cinetica finale è maggiore di quella iniziale mentre se W < 0 l’energia cinetica finale è minore di quella iniziale. Questo è il caso del lavoro delle forze di attrito e pertanto, se agiscono solo tali forze, la velocità diminuisce. Infine, se W = 0, l’energia cinetica resta costante; ciò si verifica, per esempio, nel moto circolare uniforme: il lavoro della forza centripeta, unica forza agente, è nullo e quindi la velocità rimane costante in modulo.

Sottolineamo che W rappresenta il lavoro totale. Se è noto come varia la forza lungo la traiettoria, possiamo calcolare il lavoro e quindi il modulo della velocità in ciascun punto (se conosciamo quella iniziale). Viceversa, se misuriamo le velocità iniziale e finale, possiamo tramite (2.15) dedurre il lavoro compiuto dalle forze agenti.

Si faccia attenzione al fatto che la nozione di lavoro, e quindi di variazione di energia cinetica, è necessariamente legata a quella di spostamento, secondo la definizione (2.13). Se non c’è spostamento non può esserci lavoro, qualunque sia la forza applicata (mentre può esserci spostamento senza lavoro). Quando si spinge un corpo e questo non si sposta perché è presente un attrito statico, non c’è lavoro né motore né resistente, così come non si compie lavoro quando si spinge con una mano contro un muro. In questi casi la sensazione di fatica è legata allo stato di tensione dei muscoli che richiede un consumo di energia chimica, ma, ripetiamo, il lavoro meccanico è nullo.

Unità di misura

Il lavoro è il prodotto di una forza per uno spostamento e quindi l’unità di misura del lavoro, e dell’energia cinetica come di ogni altra forma di energia, è newton · metro. Si tratta di una unità molto importante che si chiama joule ( pronuncia corretta giul! ) ed è espressa dal simbolo J = N m.

L’unità di misura della potenza è il watt, simbolo W; per definizione W = J/s = N m s^–1, J = Ws.

Multipli comunemente usati sono il chilojoule, kJ = 10³ J, megajoule MJ = 10⁶ J, chilowatt kW = 10³ W, megawatt MW = 10⁶ W.

Per il lavoro, soprattutto elettrico, è in uso anche l’unità chilowattora: 1 kWh = 10³ W · 3600 s = 3.6 · 10⁶ J.

Storicamente, una unità di potenza assai usata in passato e ora proibita è il cavallo-vapore, esistente in due versioni, quello tecnico (1 cv = 735.5 W) e quello britannico (1 hp = 745.7 W).

Se riprendiamo le definizioni di energia cinetica e di quantità di moto,

vediamo che tra energia cinetica e modulo della quantità di moto sussistono le relazioni

In questo paragrafo abbiamo introdotto per la prima volta il concetto di energia, nel caso particolare quella cinetica; in seguito troveremo altre forme di energia (energia potenziale legata ai vari tipi di forze). Tutte le leggi con cui vengono definite le varie forme di energia contengono sempre la variazione di energia e pertanto tali quantità possono essere definite a meno di una costante. Per esempio l’energia cinetica di un punto potrebbe essere scritta come 1/2 m v² + costante, senza modificare la (2.15) in quanto nella differenza la costante scompare. Però si avrebbe che questa forma di energia, legata al movimento, sarebbe non nulla anche se v = 0, il che non ha molto senso. Poniamo dunque, in questo caso, la costante eguale a zero.

Il lavoro è la manifestazione dell’azione di una forza ed è quindi conseguenza dell’interazione con l’ambiente circostante. Si parla pertanto di lavoro scambiato e non si dice mai che un sistema possiede lavoro.

Si parla invece di energia posseduta dal sistema, che viene modificata dall’interazione con l’ambiente esterno. Un effetto misurabile dell’interazione è la variazione di energia.