3.4 Moto di trascinamento rettilineo accelerato

Assumendo la stessa condizione geometrica del sistema O' rispetto al sistema O vista nel precedente paragrafo, supponiamo ora che O' abbia una accelerazione costante a_{O '} = a_t e una velocità iniziale v_in , ambedue parallele e concordi all’asse x ≡ x'. La posizione e la velocità di O' sono quindi espresse da

Le formule di trasformazione (3.11) e (3.12) diventano

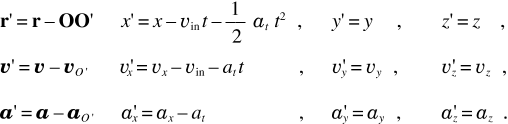
Come nel caso del moto di trascinamento rettilineo uniforme, anche ora illustriamo con esempi alcune semplici situazioni. Caratteristica distintiva è la diversità delle accelerazioni nei due sistemi, O inerziale e O' non inerziale, e quindi la diversità delle forze agenti, con conseguente comparsa delle forze d’inerzia secondo (3.10).

ESEMPIO 3.4

Il sistema O' è solidale ad un carrello che si muove con accelerazione a_t positiva rispetto al sistema O (nella situazione geometrica della figura 3.2). All’istante t = 0, quando O e O' coincidono, un punto materiale viene lasciato cadere da una piattaforma alta h solidale al carrello. Descrivere il moto di caduta visto da O e da O', calcolando in particolare dove cade il punto.

Soluzione

Consideriamo prima cosa vede l’osservatore inerziale. All’istante t = 0 il punto materiale è ad altezza h e possiede la velocità iniziale del carrello, cioè v_in , parallela all’asse x; negli istanti successivi esso è sottoposto soltanto alla forza di gravità. La traiettoria osservata è parabolica e valgono le seguenti equazioni:

Il tempo di caduta è $t_c=\sqrt{2h/g}$ e lo spazio percorso lungo l’asse x è x_c = v_in t_c . Nello stesso tempo il carrello è avanzato di x_{O '} = v_in t_c + ¹/₂ a_t $t_c^2$ . Pertanto il punto materiale tocca il pavimento del carrello più indietro rispetto a O' della quantità

Nella figura 3.7 è rappresentata la distanza tra il punto e O' nell’istante in cui il punto tocca il pavimento; la linea punteggiata è la traiettoria vista da O, mentre gli assi tratteggiati danno la posizione iniziale del sistema O' (coincidente con O).

Figura 3.7

Se fosse v_in = 0, l’osservatore O vedrebbe una caduta rettilinea, ma la distanza d sarebbe la stessa, essendo questa indipendente da v_in .

Applicando le formule di trasformazione scritte all’inizio del paragrafo possiamo dedurre cosa vede O':

Il risultato, indipendente da v_in , mostra come anche in O' l’accelerazione sia costante, ma diversa da g. Essa vale

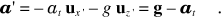
La velocità è proporzionale all’accelerazione, v' = a't. Pertanto O' osserva un moto di caduta rettilineo uniformemente accelerato nel piano x', z' lungo la retta di equazione

Il punto materiale tocca il pavimento del carrello (z' = 0) nella posizione

cioè all’indietro rispetto a O' della stessa quantità calcolata in O. L’angolo formato dalla linea di caduta con l’asse z' è

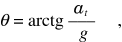
come mostrato nella figura 3.8.

Figura 3.8

Secondo O l’osservazione di O' si spiega semplicemente col fatto che O' si muove di moto accelerato. Invece O' per spiegare il moto deve aggiungere alla forza peso mg la forza apparente – ma_t ; la somma delle due forze è eguale a ma'. Se identifichiamo con la verticale la linea di caduta libera dei corpi, nel sistema O' c’è una verticale apparente che forma l’angolo θ con la verticale inerziale; un filo a piombo sul carrello si disporrebbe ad angolo θ rispetto all’asse z'. Dalla misura di θ si può dedurre il valore di a_t e determinare che il moto di trascinamento è accelerato; se fosse a_t = 0, sarebbe anche θ = 0 e d = 0, il punto cadrebbe lungo l’asse z', come nella figura 3.6 dell’esempio 3.3.

Visualizza soluzione

ESEMPIO 3.5

Un punto materiale di massa m è posto sul pavimento liscio di un carrello che avanza con accelerazione a_t rispetto al sistema inerziale O (figura 3.9). Ad un estremo del carrello è fissata una molla di costante elastica k. Descrivere le osservazioni di O e O'.

Soluzione

Nel sistema inerziale si osserva la seguente successione di eventi. Il punto resta fermo mentre il carrello gli scorre sotto (non c’è attrito) fino a quando l’estremo libero della molla lo raggiunge. La molla inizia allora a comprimersi e il punto a muoversi; a regime il punto è fermo rispetto al carrello e si muove con accelerazione a_t rispetto a O, la molla è compressa della quantità x_c = ma_t /k: infatti è la forza elastica della molla che applicata al punto gli comunica l’accelerazione a_t (kx_c = ma_t ).

Per l’osservatore O', solidale al carrello, inizialmente il puntoè in moto con accelerazione – a_t (in effetti a' = a – a_t = – a_t dato che a = 0). Ad un certo istante il punto raggiunge la molla che inizia a comprimersi e alla fine il punto è fermo, con la molla compressa della quantità x_c . O' conclude che sul punto, apparentemente libero, agisce invece la forza – ma_t che viene bilanciata, raggiunto l’equilibrio statico, dalla forza elastica della molla: kx_c = ma_t .

Notiamo che dalla misura di x_c si può dedurre il valore di a_t . La molla di questo esempio, come il filo a piombo del precedente, costituisce in sostanza un accelerometro, che misura l’accelerazione del sistema non inerziale.

Figura 3.9

Visualizza soluzione

ESEMPIO 3.6

Un sistema con origine O' e asse z' verticale è solidale ad un ascensore che si muove lungo l’asse z ≡ z' di un sistema inerziale con origine in O. L’ascensore inizia a salire con accelerazione a_t , parallela e concorde all’asse z', descrive poi un moto uniforme e infine decelera con accelerazione – a_t fino a fermarsi. Se nell’ascensore si compiono esperimenti di caduta libera dei corpi, che accelerazioni a' si misurano nelle tre fasi del moto?

Soluzione

Nel sistema inerziale a = g e quindi la relazione tra le accelerazioni è

Proiettando sull’asse z' abbiamo:

Nella fase di accelerazione O' constata che i corpi cadono con un’accelerazione maggiore di quella di gravità (aumento apparente di peso), nella fase uniforme anche O' misura g, nella fase di decelerazione i corpi cadono con un’accelerazione minore di g (diminuzione apparente di peso). Si riveda a questo proposito la discussione sulla sensazione di peso nel paragrafo 2.7.

Se fosse a_t = g, come potrebbe accadere nella fase di decelerazione, oppure se l’ascensore scendesse in caduta libera, si troverebbe a' = 0: un corpo abbandonato nell’ascensore con velocità iniziale nulla resta fermo rispetto ad O'. È la cosiddetta assenza di peso, avvertita da chi sta dentro l’ascensore e dovuta ovviamente non a una scomparsa reale dell’attrazione terrestre, ma al fatto che se tutto il sistema sta scendendo con la stessa accelerazione dei corpi che ad esso si riferiscono non c’è più accelerazione relativa e, tra l’altro, vengono a mancare le sensazioni ad essa connesse. Un effetto analogo, come è ben noto, si manifesta nei satelliti artificiali che ruotano intorno alla terra.

La spiegazione dell’assenza di accelerazione di gravità è quella data da O che misura in ogni caso g e ragiona in base a (3.10), attribuendo le variazioni all’accelerazione di trascinamento di O'. Ma O', se non ha a priori questo tipo di informazioni, ragiona in modo diverso. Egli vede che in certe situazioni l’accelerazione di un corpo che cade è g, in accordo con quanto gli può essere comunicato dall’esterno, ma sperimenta anche situazioni diverse. Se si costruisce un accelerometro e lo tara opportunamente, constata che la misura fornitagli dallo strumento è proprio la correzione da apportare a g. O' postula pertanto che in certe situazioni, che è capace di mettere in evidenza, ha origine un’accelerazione supplementare che si compone con g per dare i risultati osservati ovvero che alla forza peso va aggiunto il termine –m a_suppl ; sulle cause del fenomeno non è però in grado di fare alcuna ipotesi. Notiamo che dall’esame delle misure di a' e a_suppl egli sarebbe in grado di accorgersi da solo che c’è un valore speciale, appunto g, che si ottiene sempre sommando o sottraendo i valori di a' e a_suppl ; solo in seguito a un’informazione esterna potrebbe però accorgersi che a_suppl non è altro che a_t e che quindi egli ha un modo per mettere in evidenza cosa sta succedendo al suo sistema (se il moto di O' fosse sempre uniforme egli misurerebbe sempre g e non avrebbe alcun modo per mettere in evidenza che è in movimento).

Visualizza soluzione