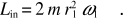
4.5 Conservazione del momento angolare

In una situazione in cui valga (4.11), cioè sia v_O ⨯ M v_CM = 0, se il momento delle forze esterne è nullo il momento angolare resta costante. La condizione M^(E) = 0 si può verificare in due casi: a) non agiscono forze esterne, il sistema è isolato: allora L si conserva rispetto a qualsiasi polo per il quale v_O ⨯ M v_CM = 0; in questa situazione, in cui è anche R^(E) = 0, si ha pure la conservazione della quantità di moto, P = costante (si osservi che R^(E) = 0 non ha come conseguenza, in generale, M^(E) = 0); b) il momento delle forze esterne è nullo rispetto ad un determinato polo, ma non rispetto a qualsiasi polo, pure in presenza di forze esterne; pertanto si ha conservazione del momento angolare solo se calcolato rispetto a quel polo (mentre, in generale, non si conserva in tali casi la quantità di moto).

Questa seconda situazione fisica sottolinea l’importanza della scelta del polo per poter risolvere determinati problemi.

L’osservazione sperimentale che, per un sistema isolato, si conserva il momento angolare (rispetto a un polo per cui v_O ⨯ M v_CM = 0 ) conferma la validità di (4.11) e quindi che sia M^{( I )} = 0. Infatti se fosse M^{( I )} ≠ 0, anche in un sistema isolato il momento angolare potrebbe non conservarsi. Di conseguenza, è corretto assumere che le forze interne a due a due abbiano la stessa retta di azione, costituiscono cioè coppie di forze con braccio nullo.

La conservazione del momento angolare di un sistema di punti materiali isolato è una proprietà molto generale: si dimostra che discende dalla caratteristica dello spazio di essere isotropo, cioè dal fatto che non esiste una direzione privilegiata.

Figura 4.17 (Esempio 4.8)

ESEMPIO 4.8

Due punti materiali di eguale massa m sono legati tra loro da una sbarretta di massa trascurabile e ruotano senza attrito in un piano orizzontale rispetto al centro della sbarretta; nella situazione iniziale la sbarretta è lunga 2r₁ e la velocità angolare ha il valore costante ω₁. Supponiamo che la sbarretta sia telescopica e che, durante il moto, la lunghezza venga portata al valore 2r₂ , con r₂ > r₁ . Calcolare il valore finale ω₂ della velocità angolare.

Soluzione

Le forze esterne al sistema, che sono le forze peso e le reazioni normali del piano, hanno momento risultante nullo rispetto al centro O del sistema, che assumiamo come polo (nel caso specifico anche R^(E) = 0). La tensione della sbarretta fornisce a ciascun punto la forza centripeta necessaria al moto circolare, ma si tratta di forze interne, con momento nullo. Possiamo dunque applicare la conservazione del momento angolare rispetto al centro O. Il momento angolare iniziale L_in è ortogonale al piano del moto, rivolto verso il lettore, e vale in modulo 2r₁ m v₁ ; dato che v₁ = ω₁ r₁ ,

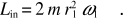
Dopo l’allungamento L_fin = 2 m $r_2^2$ ω₂ e dall’eguaglianza L_in = L_fin si ricava

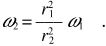
A seguito dell’allungamento il sistema rallenta. Anche per questo esempio, come per il caso della definizione dinamica della massa (paragrafo 4.3), tratteremo l’aspetto energetico nel paragrafo 4.8.

Visualizza soluzione