6.11Giroscopi

Si chiama giroscopio un corpo rigido con un punto che è mantenuto fisso da un opportuno sistema di vincoli. Il moto del giroscopio risulta in una rotazione rispetto ad un asse passante per il punto fisso, asse che in generale varia nel tempo. Il moto è piuttosto complicato e ci limitiamo, pertanto, ad esaminare solo qualche caso semplice. Avremo modo, in questo studio, di utilizzare le nozioni del paragrafo 6.10.

Figura 6.50

1º Caso

Il punto fisso coincide con il centro di massa, non ci sono momenti esterni rispetto al centro di massa (M = 0) e la rotazione avviene attorno ad un asse centrale d’inerzia, per cui L = Iω .

Tale situazione si realizza tramite dispositivi a sospensione cardanica, come in figura 6.50. Il giroscopio è il disco interno che ruota intorno all’asse z . L’anello esterno può ruotare attorno all’asse x , mentre quello interno attorno all’asse y . L’asse di rotazione z può essere orientato in qualsiasi direzione. Il peso del giroscopio è equilibrato dalla reazione dei supporti dell’asse x.

Dato che M = 0 , L = costante e quindi anche ω = costante. L’asse di rotazione resta fisso nel tempo.

Un’applicazione di questa proprietà si realizza negli stabilizzatori di direzione. Un giroscopio, montato su un corpo in movimento, mantiene la direzione del suo asse fisso, ad esempio posizionata, all’inizio del moto del corpo, parallelamente alla direzione da seguire.

Se il corpo devia da questa direzione cambia l’orientazione relativa tra corpo e giroscopio. Questa deviazione, evidenziata da opportuni sensori, attiva il dispositivo per la correzione automatica della rotta.

2° Caso

Il punto fisso coincide con il centro di massa, la rotazione ha luogo attorno ad un asse centrale d’inerzia, L = Iω , ma agisce rispetto al punto fisso un momento esterno.

Precessione del giroscopio

Avendo come riferimento la figura 6.50, supponiamo che l’asse di rotazione sia orizzontale e che venga applicata una forza verticale, come in figura 6.51a. Il momento rispetto al centro di massa è M = r × F e giace in un piano orizzontale. la variazione di L è dL = M dt, parallela a M: l’asse si sposta in un piano orizzontale e non verso il basso (L, costante in modulo, precede rispetto ad un asse verticale con velocità angolare Ω tale che M = Ω × L). Se invece la forza applicata è orizzontale (figura 6.51b) l’asse ruota in un piano verticale.

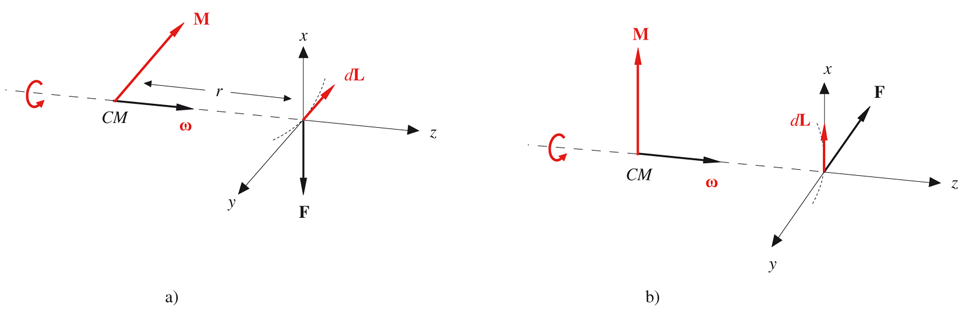
FIGURA 6.51

Il comportamento sarebbe ben diverso se fosse ω = 0: lo spostamento dell’asse seguirebbe F e non sarebbe a 90° rispetto a F, i momenti sarebbero ancora quelli disegnati, ma sia L che dL risulterebbero paralleli a M.

Figura 6.52

Figura 6.53

3° Caso

Il punto fisso coincide con il centro di massa, non ci sono momenti esterni, però l’asse di rotazione non è un asse centrale d’inerzia, L e ω non sono paralleli. Nel dispositivo di figura 6.50 si può realizzare questa situazione applicando un impulso all’asse di rotazione con il che il momento dell’impulso fa cambiare L, rendendolo non parallelo all’asse di rotazione.

Dalla condizione M = 0 si ha sempre che L è costante in direzione e modulo. Inoltre, non essendoci attriti, l’energia cinetica di rotazione resta costante. Da (6.33) segue ω · L = costante: la proiezione di ω sulla direzione fissa di L deve restare costante durante il moto. Pertanto la punta del vettore ω sta sempre su un piano ortogonale a L (figura 6.53). D’altra parte la punta di ω descrive l’ellissoide dell’energia (6.34). Poinsot ha dimostrato che l’ellissoide e il suddetto piano hanno un solo punto in comune in ogni istante e che durante il moto l’ellissoide rotola senza strisciare sul piano.

Nutazione

Nei casi più semplici ω ruota rispetto a L con un moto di precessione e ruota rispetto all’ellissoide dell’energia, cioè non ha una posizione costante nel corpo. In questo tipo di moto, che si chiama nutazione, vediamo dunque il giroscopio ruotare rispetto ad un asse che non è fisso rispetto al giroscopio stesso e che a sua volta ruota rispetto ad una direzione fissa.

Figura 6.54

4° Caso

Il punto fisso O è diverso dal centro di massa e quindi, rispetto a O, è diverso da zero il momento della forza peso.

L’esempio tipico è costituito dal moto di una trottola (figura 6.54). Il punto fisso, assunto come polo, è il punto di contatto della trottola con il piano di appoggio. L’asse di rotazione, che è un asse centrale d’inerzia, passa per O e per il centro di massa. Abbiamo L = Iω con ω costante in modulo.

Il momento della forza peso è M = r × m g, mentre il momento della reazione del piano è nullo. Pertanto

e, siccome L è costante in modulo, vale anche la (6.11):

Ω è la velocità angolare di precessione del vettore L , ovvero dell’asse di rotazione della trottola, rispetto all’asse verticale passante per O. Eguagliando

La velocità angolare di precessione è inversamente proporzionale alla velocità angolare della trottola. Il periodo del moto di precessione è

La precessione descritta qui è analoga a quella vista nel secondo caso. Il fenomeno si verifica quando è applicata all’asse di rotazione una forza costante con momento normale all’asse.

Osserviamo, anche se a posteriori, che nell’analisi del moto della trottola abbiamo fatto un’approssimazione: L non coincide completamente con Iω perché il corpo, oltre a ruotare attorno all’asse passante per O e per il centro di massa, ruota anche rispetto ad un asse verticale. Tuttavia, se ω è grande la precessione è molto lenta e il suo contributo al momento angolare è piccolo.

Se l’asse di rotazione non è un asse centrale di inerzia alla precessione si aggiunge la nutazione. In questo caso la punta di ω non descrive la circonferenza della figura 6.54, ma oscilla rispetto a questa, salendo e scendendo (figura 6.56).