7.4 Torsione. Pendolo e bilancia di torsione

Consideriamo ancora una sbarra cilindrica di raggio r e lunghezza l, bloccata su una base, e applichiamo all’altra base una coppia di forze con momento M, parallelo all’asse della sbarra, che risulta così sottoposta a torsione. Il valore di M necessario per far ruotare la base inferiore rispetto a quella superiore di un angolo θ si ricava dall’espressione

L’effetto di torsione dipende fortemente dalle dimensioni trasversali: con una sbarra molto sottile, ad esempio un filo, si ottiene una deviazione misurabile anche con l’applicazione di un momento molto piccolo. La dipendenza da G significa che la torsione ha caratteristiche simili allo scorrimento longitudinale della figura 7.11.

Figura 7.12

La reazione elastica della sbarra si manifesta con un momento –M, il cui modulo vale quindi –kθ, cioè proporzionale all’angolo di torsione. Su questo fatto si basano sia il pendolo che la bilancia di torsione.

Per effettuare la torsione il momento esterno compie il lavoro (6.17)

immagazzinato nel sistema come energia potenziale elastica.

Esempio 7.7

Determinare il momento necessario per provocare la torsione di θ = 1° di una sbarra cilindrica di ferro (G = 8.0 · 10¹⁰ N/m² · rad) con r = 1 cm e l = 1 m.

Soluzione

Il coefficiente k nella (7.6) vale

Dato che θ = 1° corrisponde a 1.7 · 10^–2 rad, M = 21.4 Nm.

Visualizza Soluzione

Esempio 7.8

Un albero motore lungo l = 1 m gira con velocità angolare ω = 104.7 rad/s (10³ giri/minuto) fornendo una potenza P = 10 kW. La torsione dell’albero non deve superare θ = 1° = 1.7 · 10^–2 rad. Calcolare il valore minimo che deve avere il diametro dell’albero, fatto di acciaio con G = 8.5 · 10¹⁰ N/m² · rad.

Soluzione

Dal punto di vista dinamico siamo in una situazione di equilibrio in cui il momento motore eguaglia il momento resistente e l’albero gira con velocità angolare costante. La potenza P è eguale a Mω da cui si ricava M = 95.5 Nm. L’albero subisce torsione durante il funzionamento e a regime il momento elastico di torsione eguaglia M (un caso analogo si ha quando si applica una forza F ad una molla che a sua volta tira un corpo sottoposto ad attrito: in regime di moto uniforme F = kx = F_att). Pertanto

Visualizza Soluzione

Pendolo di torsione

Un pendolo di torsione si realizza sospendendo un corpo solido a un filo; generalmente il punto di aggancio coincide con il centro di massa. Per esempio, un possibile pendolo di torsione consiste in un disco sospeso al centro (figura 7.13), essendo il filo verticale e il disco in un piano orizzontale. Se ruotiamo il disco di un angolo θ, mantenendolo orizzontale, il filo di sospensione subisce una torsione e sviluppa un momento elastico – kθ, con k dato da (7.6). Se ora lasciamo libero il corpo, esso si mette in rotazione sotto l’azione del momento elastico, secondo l’equazione

dove I è il momento d’inerzia del sistema rispetto all’asse di rotazione, coincidente col filo. La soluzione dell’equazione

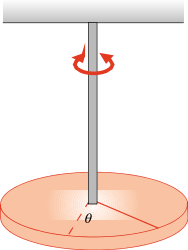
Figura 7.13

è data da θ = θ ₀ sen (ω t + ϕ ), con $\omega =\sqrt{\frac{k}{I}}$ Il sistema descrive una oscillazione armonica.

Si noti che, a differenza del pendolo semplice e del pendolo composto, non dobbiamo imporre, per avere un moto armonico, una piccola ampiezza di oscillazione, perché il filo anche con una torsione di parecchi giri sviluppa un momento proporzionale all’angolo. L’unica limitazione è di essere in condizioni di comportamento elastico del filo in torsione.

Durante l’oscillazione del pendolo di torsione si può applicare la legge di conservazione dell’energia meccanica (trascurando l’attrito dell’aria e dissipazioni di energia nel filo). Nella generica posizione individuata dall’angolo θ si utilizza (7.7) e si scrive

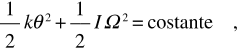
dove Ω è la velocità angolare e la costante è eguale, per esempio, alla massima energia potenziale ¹/₂ kθ² ₀ ; dall’eguaglianza si ricava Ω (θ).

Citiamo due applicazioni pratiche, basate sulla misura del periodo di oscillazione $T=2\pi /\omega =2\pi \sqrt{I/k}$ . Se è noto il momento d’inerzia si ottiene la costante k e quindi il modulo di rigidità del materiale che costituisce il filo. Invece, se è noto k si determina I; questo metodo è utile nel caso di lastre di forma qualsiasi (la posizione del centro di massa si trova con i metodi del paragrafo 6.15).

Bilancia di torsione. Esperimento di Cavendish

Figura 7.14

Su un principio analogo si basa la bilancia di torsione: si sfrutta il fatto che un filo sviluppa un momento di reazione alla torsione calcolabile dall’angolo di torsione e che in equilibrio il momento elastico è eguale al momento esterno, che ha causato la torsione. Se questo momento è dato dall’applicazione di una coppia di forze di braccio l (l potrebbe essere la lunghezza di un’asta sospesa al centro e che quindi costituisce la bilancia di torsione), deve essere Fl = kθ . Dalla misura dell’angolo di equilibrio θ si può calcolare il valore di F.

La bilancia di torsione risulta uno strumento molto sensibile, in grado cioè di misurare forze molto piccole (fino a 10^–9 N ); storicamente essa è servita a Coulomb (1785) per determinare la forza che si esercita tra cariche elettriche e a Cavendish (1788) per misurare la costante γ nella (5.1).

Nell’esperimento di Cavendish due piccole masse sferiche sono fissate agli estremi di un’asticciola, sospesa per il centro ad un filo (questa è la bilancia). Due masse sferiche molto maggiori sono poste vicino alle masse piccole, come in figura 7.15 che è una vista dall’alto, cioè lungo il filo.

Le forze di attrazione gravitazionale sulle masse piccole formano una coppia che fa ruotare la bilancia fino al raggiungimento di una posizione di equilibrio, in cui il momento gravitazionale eguaglia il momento di torsione. Successivamente si inverte la posizione delle sfere grandi e in definitiva si misura l’angolo 2θ e si calcola γ. Un esempio numerico, che ci permette di valutare la difficoltà dell’esperimento, è svolto qui di seguito. Ricordiamo che solo dopo la determinazione di γ è stato possibile calcolare la massa della terra.

Figura 7.15

Esempio 7.9

In un esperimento come quello di Cavendish le sfere piccole hanno massa m₁ = 0.05 kg, le sfere grandi m₂ = 500 kg, la lunghezza dell’asta è d = 80 cm, la distanza tra i centri di una sfera grande e della piccola ad essa vicina è R = 20 cm. Il filo è di alluminio, lungo l = 1 m e di raggio r = 0.1 mm. Calcolare il periodo della bilancia di torsione e l’angolo di deviazione, utilizzando il valore noto di γ.

Soluzione

La costante elastica del filo è

il momento d’inerzia della bilancia vale, supponendo le sfere piccole puntiformi,

È dunque necessario un tempo dell’ordine di 100 s per raggiungere l’equilibrio. La forza tra una coppia di sfere è

e il momento rispetto al centro della bilancia di torsione è

k A seguito della rotazione le sfere piccole si avvicinano a quelle grandi di ΔR = θ d/2 = 3.4 mm. L’attrazione aumenta leggermente e si ha un’ulteriore piccola deviazione. L’effetto finale è ~ 8.8 · 10^–3 rad.

Visualizza Soluzione