8.5 Liquido in rotazione

Consideriamo un liquido in un recipiente cilindrico posto in rotazione rispetto all’asse verticale z, che coincide con l’asse del cilindro; la velocità angolare ω è costante. Si osserva che dopo un certo tempo tutto il liquido ruota rigidamente insieme al recipiente e che la superficie libera non è più piana, ma concava. Vogliamo determinare la forma della superficie libera.

Ciascun elemento di liquido descrive un’orbita circolare e quindi è sottoposto a una forza radiale, diretta verso l’asse di rotazione, pari a ρdVω²r, dove r è la distanza dall’asse dell’elemento considerato, di massa dm = ρdV.

Per ricondurci a una situazione di equilibrio statico, che sappiamo trattare, ci poniamo in un sistema di riferimento ruotante con il liquido attorno all’asse z. Tale sistema non è inerziale e dobbiamo quindi considerare anche la forza apparente centrifuga, radiale e diretta verso l’esterno.

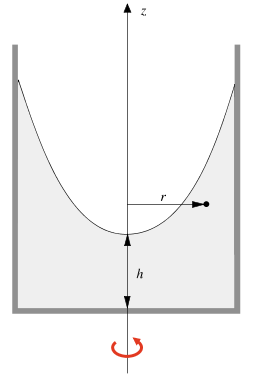
Figura 8.17

In questo sistema un qualsiasi elemento di liquido è in equilibrio statico sotto l’azione delle forze di volume, dmg e dmω²ru_r , e delle forze di pressione dovute agli elementi di liquido circostanti; u_r rappresenta il versore della direzione radiale, orientata verso l’esterno. Osserviamo che

dove x e y sono le coordinate dell’elemento di liquido in un piano ortogonale a z. L’energia potenziale per unità di massa delle forze di volume, entrambe conservative, è data da

e infatti si verifica subito che – ∇E_{p, m} mento di liquido, g + ω² r u_r .

è eguale alla forza per unità di massa agente sull’eleLa superficie libera del liquido è una superficie equipotenziale e la sua equazione è quindi determinata dalla condizione

Per determinare il valore della costante osserviamo che sull’asse (r = 0 ovvero x = y = 0) l’altezza del liquido rispetto al fondo del recipiente è z = h; la costante vale pertanto g h = E_{p, m} (0, 0, h ) e in definitiva

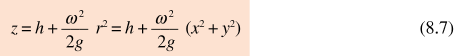
è l’equazione della superficie libera, che risulta essere un paraboloide di rotazione.

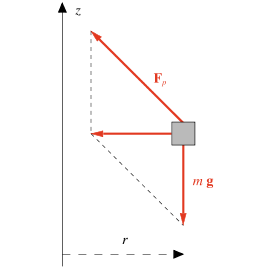
Figura 8.18

Il valore di h, altezza del vertice del paraboloide rispetto al fondo, è facilmente calcolabile. Il liquido in quiete (ω = 0 ) occupa il volume π R²d con R raggio del cilindro. In rotazione il volume dell’intercapedine cilindrica alta z e compresa tra i raggi r e r + dr è dato da

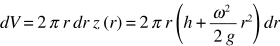
e il volume totale sotto il parabolide è

La massa nel processo non cambia; se la densità resta costante, il volume appena calcolato deve essere eguale a π R²d e si trova

L’altezza h dipende da ω e la sua misura può essere utilizzata come un tachimetro per la velocità angolare. Il massimo valore ω_M misurabile si ha per h = 0 : ω_M = 4gd/R².

Studiamo ora il moto in un sistema di riferimento inerziale; il liquido rispetto a tale sistema non è più in quiete e non possiamo usare (8.4).

La forza agente sull’elemento dm = ρdV di liquido in rotazione è la risultante della forza peso (forza di volume) e delle forze di superficie e deve essere centripeta, cioè valere – ρ dV ω ² r u_r , come abbiamo già rilevato all’inizio del paragrafo. Lungo la direzione verticale le forze agenti sono in equilibrio e quindi

come sappiamo da (8.3). La forza radiale, non nulla, è dovuta alle differenze di pressione:

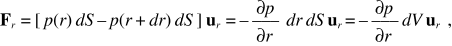
dove dS rappresenta la superficie dell’elemento, di volume dV = dr dS. Ponendo F_r eguale a – ρ dV ω² r u_r si ottiene

La pressione dunque cresce radialmente nel liquido in rotazione. La funzione p (r, z ), le cui derivate parziali soddisfano (8.8) e (8.9), è

dove k rappresenta la pressione sul fondo del recipiente e sull’asse di rotazione, cioè per z = r = 0. Se p₀ è la pressione esterna agente sulla superficie libera, k = p (0, 0) = p₀ + ρ g h. Quindi lungo la superficie libera, che è isobarica alla pressione p₀ , deve essere

che è la (8.7) già ricavata.

L’origine della forza centripeta necessaria alla rotazione del liquido è nella variazione radiale della pressione. Se nel liquido è sospeso un corpuscolo con densità ρ' ≠ ρ l’azione della pressione, esercitata dal liquido circostante, è sempre la stessa, però la forza centripeta ρVω ² r può essere troppo grande o troppo piccola per mantenere il corpuscolo, di massa ρ'V, sull’orbita circolare di raggio r. Pertanto il corpuscolo si sposterà verso l’asse di rotazione se ρ' < ρ mentre se ne allontanerà se ρ' > ρ.

Centrifugazione

Su questo risultato, che è un’estensione del principio di Archimede, si basa il metodo di separazione per centrifugazione di sostanze in sospensione in un liquido, frequentemente usato in biologia. In appositi dispositivi, detti ultracentrifughe, si raggiungono valori di ω dell’ordine di 10⁴ rad/s ≅ 10⁵ giri/minuto, riuscendo a separare sostanze con densità poco diversa da quella del liquido (differenze relative dell’ordine di 10^–2).